过程
考虑这样一个问题:给你一棵树,(q)个询问,每个询问有(k)个点,问你与这(k)个点有关的问题。(qleq 10^5,sum k leq 10^5)以下以求这(k)个点中所有两点间最短路径之和为例。
容易想到朴素求法,对于每一个询问,将每个点作标记,每次求每两个点的(lca),再求距离。这样做的复杂度大概是(O(qk^2logn)) 我也不确定这样对不对反正大概就是这样 需要优化。
接下来我们希望能优化出一个只与每次询问的点的个数有关的东西。注意到不涉及到询问的点是对答案不造成影响的,那把关键点提出来(把询问的点称为关键点),并保留它们之间的父子关系,这样又可以建出一棵树,这样建出来的树就被称为虚树。
对于每一次询问,我们将所有关键点先按(dfs)序排序,然后一个一个插入新的树里,对于相邻的两个关键点,需要插入的点可能有三个:两个关键点以及他们的(lca)。(lca)是为了保持父子关系的,所以为了区分关键点,关键点要打上标记。
如何插入呢?我们利用一个数据结构——栈。栈里保证所有在栈里的元素都是在一条链上并且有一定的顺序。
比如一棵树和初始的栈是这样的:1号节点首先入栈。
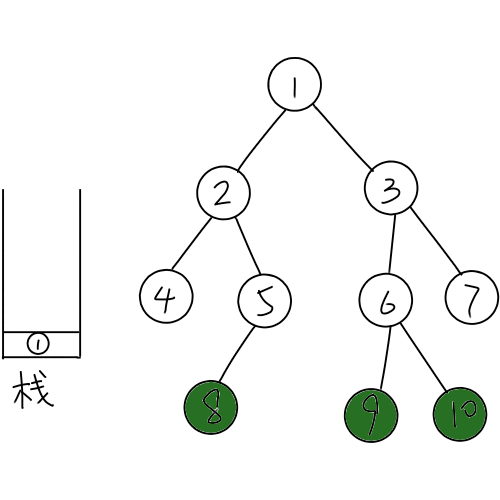
关键点是(8.9.10),排完序之后是(8.9.10)
接下来插入(8)号节点,求它跟栈顶元素的(lca)(因为栈顶元素除了1就是其他的关键点),发现(lca)已经入栈,那么只需要将(8)号节点入栈。
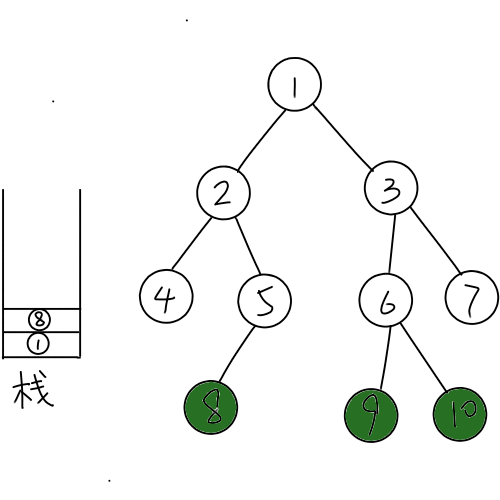
插入(9)号节点,发现跟栈顶元素(8)号节点的(lca)是(1)号节点,于是退栈并在栈中相邻的元素连边,直到栈顶元素的下一个元素(deep)小于(lca)的(deep)。(所以样例情况不需要退栈)。接下来比较栈顶元素的(deep)和(lca)的(deep),如果相等,直接插入(9)号节点即可,如果大于,则需要在(lca)和栈顶元素之间连边,再退栈,加入(lca)、(9)号节点。
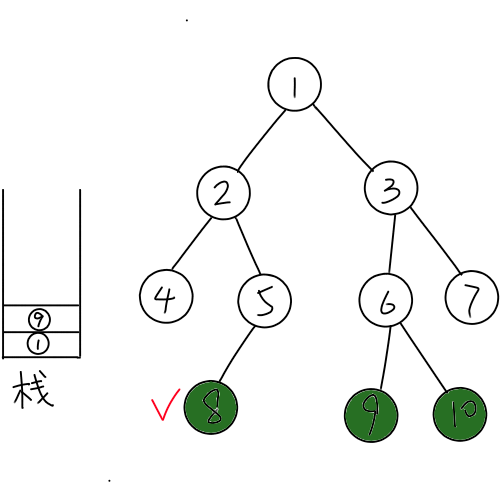
同理,插入(10)号节点。
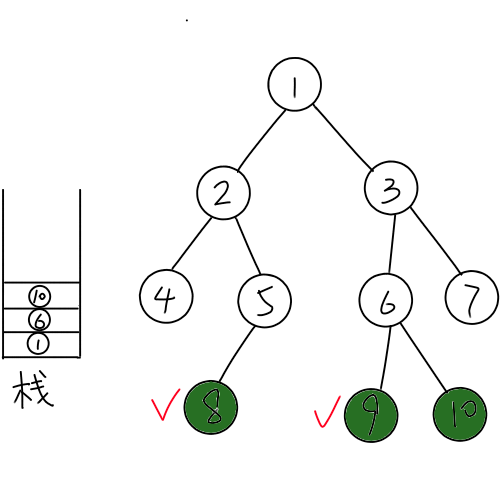
最后再将栈退完并且连边就好啦。
inline void insert (int x) {//插入元素x
if (top==1) {//1号元素也有可能是栈顶元素
if (st[top]!=x) st[++top]=x;
return;
}
int lca=LCA(st[top],x);
if (st[top]==lca) {st[++top]=x;return;}
while (top>1&&dep[st[top-1]]>=dep[lca])g[st[top-1]].pb(st[top]),top--;
if (dep[st[top]]>dep[lca]) g[lca].pb(st[top]),top--;
if (st[top]!=lca) st[++top]=lca;
st[++top]=x;
}
建好了虚树之后,树上的操作就很简单啦。对于例子来说,记录下每个子树中的关键点到对应根节点的距离和再乘兄弟子树的关键点个数就好。