题目描述
如题,已知一个数列,你需要进行下面三种操作:
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含三个整数N、M、P,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:
输出包含若干行整数,即为所有操作3的结果。
输入输出样例
输入样例#1: 复制
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4输出样例#1: 复制
17
2说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^)
样例说明:
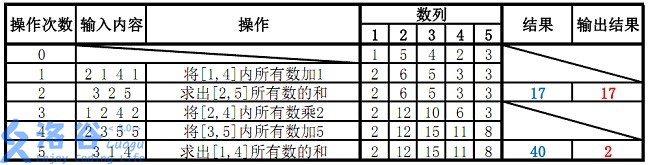
故输出应为17、2(40 mod 38=2)
AC代码
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <limits.h>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <string>
#define ll long long
#define ull unsigned long long
#define ms(a) memset(a,0,sizeof(a))
#define pi acos(-1.0)
#define INF 0x7f7f7f7f
#define lson o<<1
#define rson o<<1|1
const double E=exp(1);
const ll maxn=1e6+10;
using namespace std;
ll n,m,mod;
struct wzy
{
ll left,right,len;
ll value;
ll lazy;//加法
ll lazy1;//乘法
}p[maxn];
void push_up(ll o)
{
p[o].value=(p[lson].value+p[rson].value)%mod;
}
void push_down(ll o)
{
if(p[o].lazy||p[o].lazy1!=1)
{
p[lson].lazy=(p[lson].lazy*p[o].lazy1+p[o].lazy)%mod;
p[rson].lazy=(p[rson].lazy*p[o].lazy1+p[o].lazy)%mod;
p[lson].lazy1=(p[o].lazy1*p[lson].lazy1)%mod;
p[rson].lazy1=(p[o].lazy1*p[rson].lazy1)%mod;
p[lson].value=(p[lson].value*p[o].lazy1+p[o].lazy*p[lson].len)%mod;
p[rson].value=(p[rson].value*p[o].lazy1+p[o].lazy*p[rson].len)%mod;
p[o].lazy=0;
p[o].lazy1=1;
}
}
void build(ll o,ll l,ll r)
{
p[o].left=l;p[o].right=r;
p[o].len=r-l+1;
p[o].lazy=0;
p[o].lazy1=1;
if(l==r)
{
ll x;
scanf("%lld",&x);
p[o].value=x;
return ;
}
ll mid=(l+r)>>1;
build(lson,l,mid);
build(rson,mid+1,r);
push_up(o);
}
void update(ll o,ll l,ll r,ll v)//相加
{
if(p[o].left>=l&&p[o].right<=r)
{
p[o].lazy=(p[o].lazy+v)%mod;
p[o].value=(p[o].value+v*p[o].len)%mod;
return ;
}
push_down(o);
ll mid=(p[o].left+p[o].right)>>1;
if(r<=mid)
update(lson,l,r,v);
else if(l>mid)
update(rson,l,r,v);
else
{
update(lson,l,mid,v);
update(rson,mid+1,r,v);
}
push_up(o);
}
void update1(ll o,ll l,ll r,ll v)//相乘
{
if(p[o].left>=l&&p[o].right<=r)
{
p[o].value=(p[o].value*v)%mod;
p[o].lazy=(p[o].lazy*v)%mod;
p[o].lazy1=(p[o].lazy1*v)%mod;
return ;
}
push_down(o);
ll mid=(p[o].left+p[o].right)>>1;
if(r<=mid)
update1(lson,l,r,v);
else if(l>mid)
update1(rson,l,r,v);
else
{
update1(lson,l,mid,v);
update1(rson,mid+1,r,v);
}
push_up(o);
}
ll query(ll o,ll l,ll r)
{
if(p[o].left>=l&&p[o].right<=r)
return p[o].value;
ll mid=(p[o].left+p[o].right)>>1;
push_down(o);
if(r<=mid)
return query(lson,l,r);
else if(l>mid)
return query(rson,l,r);
else
return query(lson,l,mid)+query(rson,mid+1,r);
}
int main(int argc, char const *argv[])
{
ios::sync_with_stdio(false);
scanf("%d%d%d",&n,&m,&mod);
build(1,1,n);
int _;
ll a,b,c;
while(m--)
{
scanf("%d",&_);
if(_==3)
{
scanf("%lld%lld",&a,&b);
printf("%lld
",query(1,a,b)%mod);
}
else if(_==2)
{
scanf("%lld%lld%lld",&a,&b,&c);
update(1,a,b,c);
}
else if(_==1)
{
scanf("%lld%lld%lld",&a,&b,&c);
update1(1,a,b,c);
}
}
return 0;
}