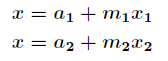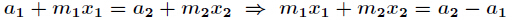第1行:1个数N表示后面输入的质数及模的数量。(2 <= N <= 10) 第2 - N + 1行,每行2个数P和M,中间用空格分隔,P是质数,M是K % P的结果。(2 <= P <= 100, 0 <= K < P)
输出符合条件的最小的K。数据中所有K均小于10^9。
3 2 1 3 2 5 3
23
对于《孙子算经》中“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”问题的求解:
- 找出三个数:从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
- 用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加15∗2+21∗3+70∗215∗2+21∗3+70∗2得到和233。
- 用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23233%105=23。这个余数23就是符合条件的最小数。
就这么简单。我们在感叹神奇的同时不禁想知道古人是如何想到这个方法的,有什么基本的数学依据吗?
我们将“孙子问题”拆分成几个简单的小问题,从零开始,试图揣测古人是如何推导出这个解法的。
首先,我们假设n1n1是满足除以3余2的一个数,比如2,5,8等等,也就是满足3∗k+2(k>=0)3∗k+2(k>=0)的一个任意数。同样,我们假设n2n2是满足除以5余3的一个数,n3n3是满足除以7余2的一个数。
有了前面的假设,我们先从n1n1这个角度出发,已知n1n1满足除以3余2,能不能使得n1+n2n1+n2的和仍然满足除以3余2?进而使得n1+n2+n3n1+n2+n3的和仍然满足除以3余2?
这就牵涉到一个最基本数学定理,如果有a%b=ca%b=c,则有(a+k∗b)%b=c(k为非零整数)(a+k∗b)%b=c(k为非零整数),换句话说,如果一个除法运算的余数为cc,那么被除数与kk倍的除数相加(或相减)的和(差)再与除数相除,余数不变。这个是很好证明的。
以此定理为依据,如果n2n2是3的倍数,n1+n2n1+n2就依然满足除以3余2。同理,如果n3n3也是3的倍数,那么n1+n2+n3n1+n2+n3的和就满足除以3余2。这是从n1n1的角度考虑的,再从n2n2,n3n3的角度出发,我们可推导出以下三点:
- 为使n1+n2+n3n1+n2+n3的和满足除以3余2,n2n2和n3n3必须是3的倍数。
- 为使n1+n2+n3n1+n2+n3的和满足除以5余3,n1n1和n3n3必须是5的倍数。
- 为使n1+n2+n3n1+n2+n3的和满足除以7余2,n1n1和n2n2必须是7的倍数。
因此,为使n1+n2+n3n1+n2+n3的和作为“孙子问题”的一个最终解,需满足:
- n1n1除以3余2,且是5和7的公倍数。
- n2n2除以5余3,且是3和7的公倍数。
- n3n3除以7余2,且是3和5的公倍数。
所以,孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1n1,从3和7的公倍数中找一个除以5余3的数n2n2,从3和5的公倍数中找一个除以7余2的数n3n3,再将三个数相加得到解。在求n1n1,n2n2,n3n3时又用了一个小技巧,以n1n1为例,并非从5和7的公倍数中直接找一个除以3余2的数,而是先找一个除以3余1的数,再乘以2。也就是先求出5和7的公倍数模3下的逆元,再用逆元去乘余数。
这里又有一个数学公式,如果a%b=ca%b=c,那么(a∗k)%b=a%b+a%b+…+a%b=c+c+…+c=k∗c(k>0)(a∗k)%b=a%b+a%b+…+a%b=c+c+…+c=k∗c(k>0),也就是说,如果一个除法的余数为cc,那么被除数的kk倍与除数相除的余数为k∗ck∗c。展开式中已证明。
最后,我们还要清楚一点,n1+n2+n3n1+n2+n3只是问题的一个解,并不是最小的解。如何得到最小解?我们只需要从中最大限度的减掉掉3,5,7的公倍数105即可。道理就是前面讲过的定理“如果a%b=ca%b=c,则有(a−k∗b)%b=c(a−k∗b)%b=c”。所以(n1+n2+n3)%105(n1+n2+n3)%105就是最终的最小解。
这样一来就得到了中国剩余定理的公式:
设正整数
两两互素,则同余方程组
有整数解。并且在模
下的解是唯一的,解为
其中
,而
为
模
的逆元。
中国剩余定理扩展——求解模数不互质情况下的线性方程组:
普通的中国剩余定理要求所有的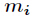
这种情况就采用两两合并的思想,假设要合并如下两个方程:
那么得到:
我们需要求出一个最小的xx使它满足:

那么x1x1和x2x2就要尽可能的小,于是我们用扩展欧几里得算法求出x1x1的最小正整数解,将它代回a1+m1x1a1+m1x1,得到xx的一个特解x′x′,当然也是最小正整数解。
所以xx的通解一定是x′x′加上lcm(m1,m2)∗klcm(m1,m2)∗k,这样才能保证xx模m1m1和m2m2的余数是a1a1和a2a2。由此,我们把这个x′x′当做新的方程的余数,把lcm(m1,m2)lcm(m1,m2)当做新的方程的模数。(这一段是关键)
合并完成:
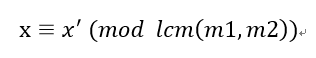
以上文字来自点击打开链接
本题AC代码:
#include <bits/stdc++.h>
const int maxn=1e3+10;
int p[maxn],m[maxn];
int main()
{
int n,k;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d%d",&p[i],&m[i]);
int res=1;
k=m[0];
for(int i=0;i<n-1;i++)
{
res=res*p[i];
while(k%p[i+1]!=m[i+1])
k+=res;
}
printf("%d
",k);
return 0;
}