第一次个人编程作业

一：超链接

Github仓库

二：实现过程、方法阐述

实现过程：

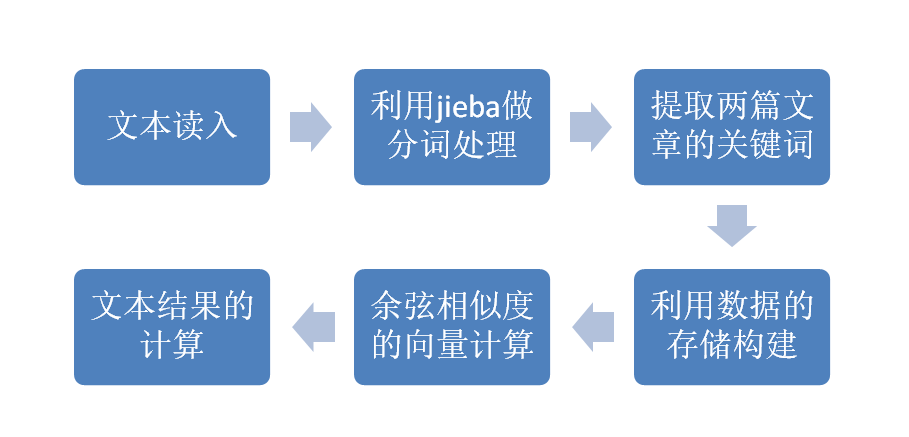
方法阐述：
编写一个文章查重方法的测试代码，在百度上搜索许久之后，发现使用余弦定理计算文本相似度是最容易理解并编写改程序的。故得以实现。
所谓的利用余弦定理，简单来说，就是用向量的方向计算来比较两篇文本的相似度，详细的解释可以参照。

三：异常处理、函数分析、性能改进

异常处理：

try:
    f=open(output,"w")
    f.write(result+"
")
    f.close()
    print("结果已存入文件夹中")
except IOError:
    print("Error: 没有找到文件或读取文件失败")

异常处理的函数，可以防止编译时地址等等出错的问题。
函数分析：

def __init__(self, target1, target2, topK=1000):
      self.target1 = target1
      self.target2 = target2
      self.topK = topK

target1和target2分别为对比的两篇文章样本，topK为将提取出前面1000个出现多次的关键字词。

def vector(self):
      self.vdict1 = {}
      self.vdict2 = {}
      top_keywords1 = jieba.analyse.extract_tags(self.target1, topK=self.topK, withWeight=True)
      top_keywords2 = jieba.analyse.extract_tags(self.target2, topK=self.topK, withWeight=True)
      for k, v in top_keywords1:
          self.vdict1[k] = v
      for k, v in top_keywords2:
          self.vdict2[k] = v

利用jieba.analyse库对文本拆分，并且得到分别出现的次数再返回这些需要用到的值。

def mapminmax(vdict):
       _min = min(vdict.values())
       _max = max(vdict.values())
       _mid = _max - _min
       for key in vdict:
           vdict[key] = (vdict[key] - _min) / _mid
       return vdict

计算相对的词频并且得到最后的数据。

def similar(self):
      self.vector()
      self.mix()
      sum = 0
      for key in self.vdict1:
          sum += self.vdict1[key] * self.vdict2[key]
      A = sqrt(reduce(lambda x, y: x + y, map(lambda x: x * x, self.vdict1.values())))
      B = sqrt(reduce(lambda x, y: x + y, map(lambda x: x * x, self.vdict2.values())))
      return sum / (A * B)

相似度的计算，利用的是文章相似度的计算公式。
性能改进：



从每个函数消耗的时间来看，总耗时2518ms，时间消耗比较大的函数有__init__,similar,vector等等函数，但是在查询了很多种方法之后，在目前我的认知来看，已经是最优的结果了，在python函数上面各种库的使用，既要保证代码的规范与简单，又要保证时间和内存的优越性，所以这已经是最好的结果了。

四：单元测试展示

下面是单元测试的执行代码

from __future__ import division
from math import sqrt
import jieba.analyse
from functools import reduce
 
if __name__ == '__main__':
    f1=open("D:PythonFirstcodeorig.txt","r",encoding='UTF-8')
    f2=open("D:PythonFirstcodeorig_0.8_add.txt","r",encoding='UTF-8')
    f3 = open("D:PythonFirstcodeorig_0.8_del.txt", "r", encoding='UTF-8')
    f4 = open("D:PythonFirstcodeorig_0.8_dis_1.txt", "r", encoding='UTF-8')
    f5 = open("D:PythonFirstcodeorig_0.8_dis_3.txt", "r", encoding='UTF-8')
    f6 = open("D:PythonFirstcodeorig_0.8_dis_7.txt", "r", encoding='UTF-8')
    f7 = open("D:PythonFirstcodeorig_0.8_dis_10.txt", "r", encoding='UTF-8')
    f8 = open("D:PythonFirstcodeorig_0.8_dis_15.txt", "r", encoding='UTF-8')
    f9 = open("D:PythonFirstcodeorig_0.8_mix.txt", "r", encoding='UTF-8')
    f10 = open("D:PythonFirstcodeorig_0.8_rep.txt", "r", encoding='UTF-8')
    t1=f1.read()
    t2=f2.read()
    t3=f3.read()
    t4=f4.read()
    t5=f5.read()
    t6=f6.read()
    t7=f7.read()
    t8=f8.read()
    t9=f9.read()
    t10=f10.read()
    f1.close()
    f2.close()
    f3.close()
    f4.close()
    f5.close()
    f6.close()
    f7.close()
    f8.close()
    f9.close()
    f10.close()
    topK = 1000
    s = Similarity(t1, t2, topK)
    result = s.similar()
    print('%.2f' % result)
    s = Similarity(t1, t3, topK)
    result3=s.similar()
    print('%.2f' %result3)
    s = Similarity(t1, t4, topK)
    result4 = s.similar()
    print('%.2f' % result4)
    s = Similarity(t1, t5, topK)
    result5 = s.similar()
    print('%.2f' % result5)
    s = Similarity(t1, t6, topK)
    result6 = s.similar()
    print('%.2f' % result6)
    s = Similarity(t1, t7, topK)
    result7 = s.similar()
    print('%.2f' % result7)
    s = Similarity(t1, t8, topK)
    result8 = s.similar()
    print('%.2f' % result8)
    s = Similarity(t1, t9, topK)
    result9 = s.similar()
    print('%.2f' % result9)
    s = Similarity(t1, t10, topK)
    result10 = s.similar()
    print('%.2f' % result10)

结果展示

五：PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	60
Estimate	估计这个计划需要多少时间	30	30
Development	开发	210	220
Analysis	需求分析	500	480
Design Spec	生成设计文档	45	40
Design Review	设计复审	30	30
Coding Standard	代码规范	60	60
Design	具体设计	120	120
Coding	具体编码	120	120
Code Review	代码复审	30	30
Test	测试	120	200
Reporting	报告	20	20
Test Report	测试报告	30	30
Size Measurement	计算工作量	20	20
Postmortem&Process Improvement Plan	事后总结，并提出过程改进过程	30	50
	合计	1425	1510

六：总结

首先在切入题目的时候就琢磨了很久，特别是第一次用测试的软件，之前完全没有用过所以折腾了好久才出来了这个东西。为了完成这次的代码作业，我看了大量的博客，疯狂的找到自己需要的文案与方法，并加以融合改进。最后在改进代码的环节上，再一次次不影响原本函数的可读性和可操作性的方面，也没有太多的地方能进行修改。这里面有太多自己需要学习的知识了，总感觉做的还不够。总之能这次在花了大量的时间的基础上，把这次的实验做到尽量的复合自己当初设计的要求。(/ω＼)