技巧总结

有关平均值的一个技巧

判断一个区间(a_n~a_m)的平均值avg是否大于一个数b，可等价为判断前缀和数组中(s_m)与(s_{n-1})的大小关系

证明：
(avg = frac{displaystyle sum_{n leq i leq m}a[i]}{m - n + 1})

(avg - b = frac{displaystyle sum_{n leq i leq m}a[i]}{m - n + 1} - b = frac{displaystyle sum_{n leq i leq m}a[i] - (m - n + 1) * b}{m - n + 1})

因为(m - n + 1 > 0), 所以(avg)与(b)的大小关系等价为(displaystyle sum_{n leq i leq m}a[i] - (m - n + 1) * b)与0的大小关系，即每一个a[i]减去b之后的和与0的关系
区间求和如果采用前缀和的方式，问题又可等价为(s_m - s_{n-1})与0的关系，即(s_m)与(s_{n-1})的大小关系

应用实例
最佳牛围栏一题中使用该技巧实现了算法的关键优化

(O(n))预处理以2为底的对数

log2[1] = 0; // 循环会将log2[1]计算为1
for (int i = 2; i <= n; ++ i) log2[i] = log2[i >> 1] + 1;

正确性证明:对于log2[x]，x只有两种可能

1. (x = 2^k)，此时(log_2x = log_22^k = log_2(2^{k-1} * 2) = log_22^{k-1} + 1 = log_2(x >> 1) + 1)

2. (x = 2^k + c)，此时(0 < c < 2^{k}), (log_2x = log_2(2^k+c))实际结果应该位于(k)到(k+1)之间，即(k.xxx)，因为我们计算对数时实际是对结果下取整，所以(log_2x = k)

   接下来证明(log_2frac{x}{2} + 1= k)。

   (frac{2^k}{2} = 2^{k - 1})； (0 < c < 2^{k}),所以(0 < frac{c}{2} < 2^{k-1})。

   根据(log_2(2^k+c) = k (0 < c < 2^{k}))可得，(log_2(2^{k-1}+d) = k - 1, (0 < d < 2^{k-1})), 所以(log_2(frac{x}{2}) = k-1), 所以证得(log_2(frac{x}{2}) + 1= k)

综上所述，(log_2[x] = log_2[x >> 1] + 1)

质数$约数转换计算方向优化时间复杂度

约数: 轻拍牛头
质数: 阶乘分解
从数据算约数，质因数分解复杂度较高
约数和质因子筛会更快

相同数字组成的数据形式的转化

所谓相同的数字，是指像11111，22222，...这种aaaa...形式的数字
我们以8888为例子，(8888 = 8 * 1111 = 8 * frac{9999}{9} = 8 * frac{10^4 - 1}{9})
所以 (aaaa... = a * frac{10^x - 1}{9})
同时x恰好就是原数据的位数
这个技巧在最幸运的数字一题中出现

mod m的情况下求最小正整数

(x % m + m) % m
应用实例见扩展欧几里得多解时取最小正整数

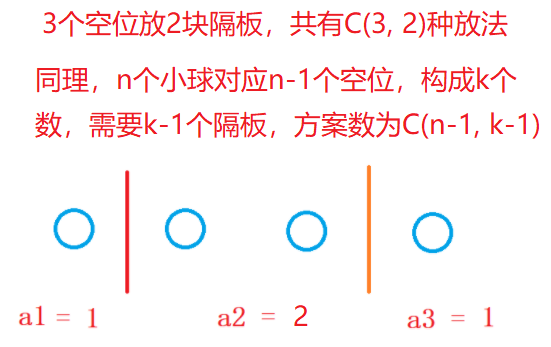
隔板法

问题类型
(a_1 + a_2 + a_3 + ... + a_k = n)
在(a_i >= 1)的情况下询问一共有多少组解(等价于正整数解)。不同顺序并不相同
eg:(k = 3, n=4)时，共有3组解

解决方法

10进制转k进制精简写法

for (int i = 0; x; x /= k, ++ i)
  s[i] += x % k;

正向求解与反向验证

有些时候，验证问题要比求解问题简单得多

北极通讯网络一题就是这个结论的最好证明
此问题可以简述为：在条件k的约束下，求解d的最优解
正向求解的思路是，构造出最小生成树，使用那k台卫星设备去掉较大的几条边，剩余边中最大的即为答案，但是由点确定边时，选择不同位置的点所确定的边也是不同的，这点是很难确定的
反向求解的思路是，假设已经确定了d的值，在图中那些<=d的边可以存在，反之不能，最终构成了多个连通块，连通块之间的通信则需要使用卫星设备，有几个连通块就需要使用几个卫星设备，通过与k进行比较，即可确定该d值是否合法
在“在条件k的约束下，求解d的最优解”这种题型下，一种解决思路是枚举d值，采用k对d进行评判，从而找到答案。利用k对d进行评判就是验证问题的过程

等式与不等式转化

(a == b <=> a <= b && a >= b)
目前已知的应用场景是差分约束，题目中给定的是等于关系，但要转换为不等关系

最大值和次大值

求一些数据中的最大值和次大值

const int INF = 0x3f3f3f3f;

int a[] = {1, 2, 3, 4};
int max1 = -INF, max2 = -INF; // 依次为最大值，次大值

for (int i = 0; i < 4; ++ i)
{
    if (a[i] > max1) max2 = max1, max1 = a[i];
    else if (a[i] != max1 && a[i] > max2) max2 = a[i];
}

遍历一维空间同时获取对应二维空间位置

实质上把一维空间当作二维空间进行for循环，同时使用一个单独的下标枚举一维空间

#include <iostream>

using namespace std;

int main() {
    int nums[81];
    for (int i = 0; i < 81; ++i) {
        nums[i] = i % 9;
        cout << nums[i];
    }

    for (int i = 0, k = 0; i < 9; ++i) {
        for (int j = 0; j < 9; ++j, ++k) cout << nums[k];
        cout << endl;
    }

    return 0;
}

距离计算

在一连续区间中，计算两个元素之间的距离有两种方案：

1. 采用计数器Counter
2. 通过下标运算

方法1代码实现细节上要明显多于方法2，即更容易出错，至于优点暂时还没遇到

构造10进制回文数

结论：

1. 对于([10^i, 10^{i + 1}))范围内的每个数(长度为(i+1))，将末尾位的其余位取反拼接到原数末尾，可以获得长度为(2i+1)的10进制回文数
2. 对于([10^i, 10^{i + 1}))范围内的每个数(长度为(i+1))，将所有位取反拼接到原数末尾，可以获得长度为(2i+2)的10进制回文数

代码实现

void get_palindrome_number() {
    vector<int> res;
    // 每次获取[10^start, 10^start - 1)
    for (int start = 1; start <= 10; start *= 10) {
        // 除末尾位其余位取反拼接到原数末尾获得长度为2*len(start)+1的回文数
        for (int i = start; i <= start * 10 - 1; ++i) {
            int num = i;
            for (int j = i / 10; j; j /= 10) // 起始先/10将末尾位删除
                num = num * 10 + j % 10;
            res.push_back(num);
        }

        // 所有位取反拼接到原数末尾获得长度为2*len(start)+2的回文数
        for (int i = start; i <= start * 10 - 1; ++i) {
            int num = i;
            for (int j = i; j; j /= 10)
                num = num * 10 + j % 10;
            res.push_back(num);
        }
    }

    for (int num : res) 
        cout << num << ' ';
    cout << endl;
}