题面:

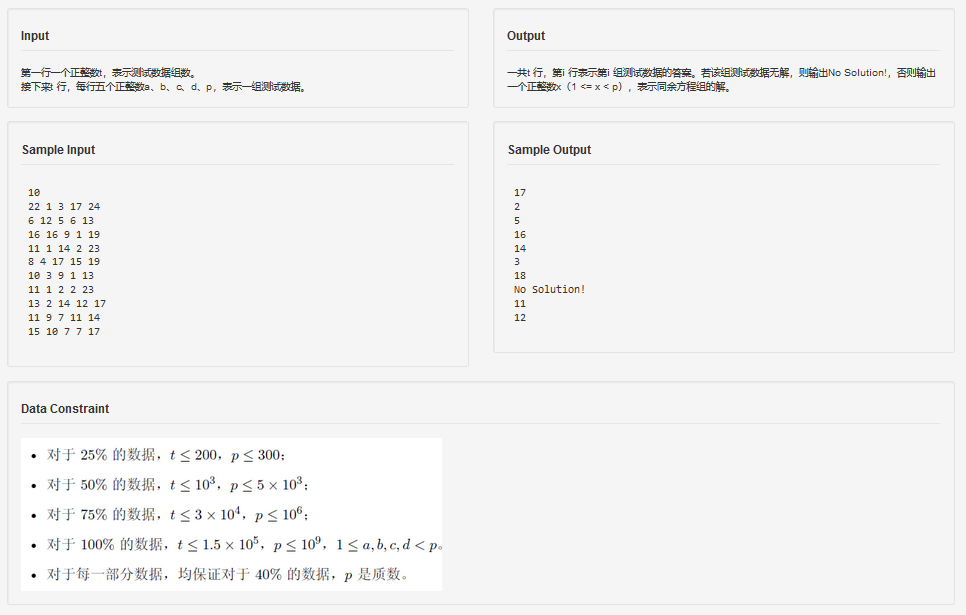
正文:
把题目中的方程组组合在一起就变成了:
(X^{a+c}equiv b cdot d (mod p))
那这时,我们假定两个数(x)和(y),使得:
(ax + cy = 1)
于是:
(X^{ax+cy}equiv X equiv b^x cdot d^y (mod p))
那我们就可以根据(ax+cy=1)跑一遍扩欧,再根据(X equiv b^x cdot d^y (mod p)),就能得出(X)了。
但是,你以为出题人这么善良吗?
(x)和(y)可能是负数,做(b^x cdot d^y) 时就相当于 (frac{1}{b^{(-x)}} cdot frac{1}{d^{(-y)}}), 因为有膜法技能同余,这里肯定出锅。
所以我们还要给(b)和(d)求个逆元,同样,也是用扩欧。