是的你没有看错,又是Tarjan(说过他发明了很多算法),那么什么是Tarjan
首先看看度娘的解释:
有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,
则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,
称为强连通分量(strongly connected components)。
是不是没有看懂,我也是
首先了解几个概念:强连通,强连通图,强连通分量
强连通:在一个有向图G中,两个点a,b,a可以走到b,b可以走到a,我们就说(a,b)强连通
强连通图:在一个有向图G中,任意两个点都是强连通
强连通分量:在一个有向图G中,有一个子图,它任意两个点都是强连通,我们就说这个子图为强连通分量,特别的,一个点也是一个强连通分量
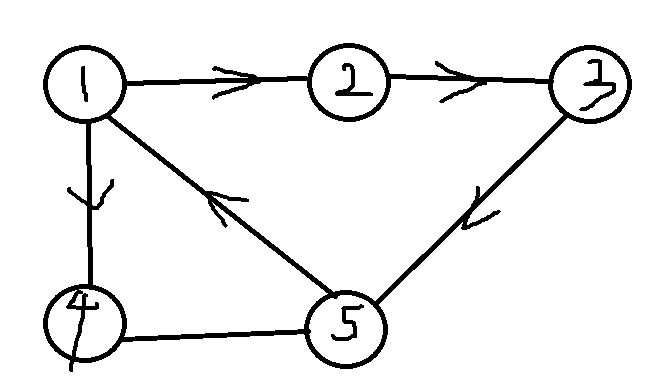
如图所示:

显然可得:1,2,3,5 构成了一个强连通分量(一个点也是)
下面进入正题,厉害的Tarjan发明的厉害的Tarjan
首先引进一个概念(以前应该都学过),时间戳,用数组dfn表示(应该不用讲吧),也就是搜索这个图的顺序(最后还是讲了)
每个节点的时间戳不同
再是一个low数组,low[x]表示以x为根的子树中,每个节点中连接的点的时间戳的最小值(可能有点难懂,但这个非常重要,是核心思想,等一下的模拟过程会详细讲述)
low的初值:low[x]=dfn[x]
那么如何储存强连通分量呢,可以用栈(学c++的有福利啦,我们有STL)

可惜我不会用,(手写栈挺好的),每次遍历到一个新节点,就把它放进栈,如果这个点有出度,就继续往下找,直到不能再找
每一次回来都要更新low值,当然是取小的那个,如果发现low[x]=dfn[x]那么它的子节点中肯定有一个连上来,既然可以过去又可以回来,很明显是一个强连通分量
那么这个x就是这个强连通分量的根节点,那么栈中间,比这个x晚进来的点就是x的子节点,那么这些点全部出栈,就组成了一个强连通分量
到这来就完了,但是好像还是没有理解透彻(反正我是这样)
那么就模拟一下
还是这张图5——>4
low[1]=dfn[1]=1,1入栈
low[2]=dfn[2]=2,2入栈
low[3]=dfn[3]=3,3入栈
low[5]=dfn[5]=4,4入栈
然后发现5连接着1,已经寻找过得了,那么就看看,谁才是真正的祖先
low[1]=1,low[5]=4,好吧,5输了,所以1是5的根节点,low[5]=min(low[5],low[1])=1
继续发现还有4,low[4]=dfn[4]=5,4入栈
但是4已经没有了出度,往回退
发现low[4]=dfn[4]那么4就是一个强连通分量的根节点(其实也就它一个),4退栈
继续往回退:low[5]=min(low[5],low[4])=1;
继续:一直到1,low[3]=min(low[3],low[5])=1;low[2]=min(low[2],low[3])=1;
low[1]=min(low[1],low[2])=1;
发现此时low[1]=dfn[1],所以1也是一个强连通分量的根,此时发现栈里还有1,2,3,5
所以这个强连通分量为1,2,3,5
1还有一个出度:4
寻找4,low[4]=dfn[4]=6,发现没有出度
low[4]=dfn[4],所以4是一个强连通分量的根节点(还是只有他一个),退栈
往回退,low[1]=min(low[1],dfn[4])=1;
这样就完了吗?
万一还有图没有遍历到呢
所以要加一个语句:
for(int i=1;i<=number;i++) if(!dfn[i])Tarjan(i);
以上的模拟过程用程序表示就是:
void Tarjan(int x){ dfn[x]=low[x]=++deep; q[++hd]=x;res[x]=1; for(int i=head[x];i;i=next[i]){ int y=ver[i]; if(!dfn[y]){ Tarjan(y); low[x]=min(low[x],low[y]); } else if(res[y])low[x]=min(low[x],dfn[y]); } if(low[x]==dfn[x]){ int sum=0; do{ res[q[hd]]=0;hd--;sum++; }while(x!=q[hd+1]); if(sum>1)ans++; } }
来一个模板题:洛谷
P2863 [USACO06JAN]牛的舞会The Cow Prom
大意是求强连通分量数量,不过注意的是,每一个点不能算,所以要加一个特判
以下是AC代码:
#include<bits/stdc++.h> using namespace std; const int N=50002; int number,m,ans=0; int tot,next[N],ver[N],head[N]; int dfn[N],low[N],deep,res[N],q[N],hd; int read(){ int s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9')w=(ch=='-')?-1:1,ch=getchar(); while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar(); return s*w; } void add(int x,int y){ ver[++tot]=y;next[tot]=head[x];head[x]=tot; } void Tarjan(int x){ dfn[x]=low[x]=++deep; q[++hd]=x;res[x]=1; for(int i=head[x];i;i=next[i]){ int y=ver[i]; if(!dfn[y]){ Tarjan(y); low[x]=min(low[x],low[y]); } else if(res[y])low[x]=min(low[x],dfn[y]); } if(low[x]==dfn[x]){ int sum=0; do{ res[q[hd]]=0;hd--;sum++; }while(x!=q[hd+1]); if(sum>1)ans++; } } int main(){ number=read();m=read(); for(int i=1;i<=m;i++){ int x=read(),y=read(); add(x,y); } for(int i=1;i<=number;i++) if(!dfn[i])Tarjan(i); cout<<ans; return 0; }