写这篇题解仅仅是因为这是第一道没看题解,一遍过的紫题 ⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄
题目背景
XS中学化学竞赛组教练是一个酷爱炉石的人。
有一天他一边搓炉石一边监考,而你作为一个信息竞赛的大神也来凑热闹。
然而你的化竞基友却向你求助了。
“第1354题怎么做”<--手语 他问道。
题目描述
你翻到那一题:给定一个烃,只含有单键(给初中生的一个理解性解释:就是一堆碳用横线连起来,横线都是单条的)。
然后炎魔之王拉格纳罗斯用他的火焰净化了一切环(???)。所有的环状碳都变成了一个碳。如图所示。
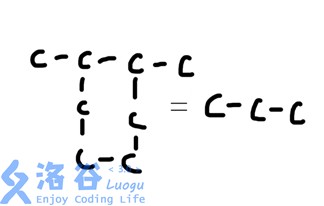
然后指定多组碳,求出它们之间总共有多少碳。如图所示(和上图没有关系)。

但是因为在考试,所以你只能把这个答案用手语告诉你的基友。你决定用二进制来表示最后的答案。如图所示(不要在意,和题目没有什么没关系)。
输入格式
第一行两个整数n,m.表示有n个点,m根键
接下来m行每行两个整数u,v表示u号碳和v号碳有一根键
接下来一个整数tot表示询问次数
接下来tot行每行两个整数,a,b表示询问的两个碳的编号
输出格式
共tot行
每行一个二进制数
输入输出样例
3 2 1 2 2 3 2 1 2 2 3
10 10
说明/提示
1<n<=10000,1<m<=50000
#(两个碳不成环)
-------------------------------------------------------小分割线-----------------------------------------------------------
一看到题目,找环,Tarjan
但是是无向边,所以普通的tarjan肯定是行不通
所以我们要加一个限定条件:
if(edge[i].to==father[now])continue;
防止它直接回到父节点
好,只要这个对了,应该都做出来了吧
接下来就是求LCA,以任意一个点作为根节点
dis[i]表示到根节点的距离,很显然,两个碳之间的数量就是:
dis[x]+dis[y]-dis[lca(x,y)]+1
一下就是代码(看起来很长,只不过是我最近不知道为什么喜欢打树剖,倍增求lca代码就短很多)
#include<bits/stdc++.h> using namespace std; #define int long long #define cg ch=getchar() const int _=50002*2; int number,edge_n,number_w,root,cnt,dis[_]; int father[_],size[_],son[_],id[_],top[_],deep[_]; int color[_],sum,q[_],hd,dfn[_],low[_],deeth,res[_]; int ver[_],nxt[_],head[_],tot,cx[_],cy[_]; int read(){ int s=0,w=1;char cg; while(ch<'0'||ch>'9')w=(ch=='-')?-1:1,cg; while(ch>='0'&&ch<='9')s=s*10+ch-'0',cg; return s*w; } void add(int x,int y){ ver[++tot]=y;nxt[tot]=head[x];head[x]=tot; } void Tarjan(int now,int fa){ low[now]=dfn[now]=++deeth;res[now]=1; q[++hd]=now; for(int i=head[now];i;i=nxt[i]){ int y=ver[i]; if(y==fa)continue; if(!dfn[y])Tarjan(y,now),low[now]=min(low[y],low[now]); else if(res[y])low[now]=min(low[now],dfn[y]); } if(dfn[now]==low[now]){ color[now]=++sum;res[now]=0; while(q[hd]!=now){ color[q[hd]]=sum;res[q[hd--]]=0; } hd--; } } void dfs1(int now,int fa,int de){ deep[now]=de;father[now]=fa;size[now]=1;id[++cnt]=now;dis[now]=dis[fa]+1; int maxx=-1; for(int i=head[now];i;i=nxt[i]){ int y=ver[i]; if(y==fa)continue; dfs1(y,now,de+1); size[now]+=size[y]; if(size[y]>maxx)maxx=size[y],son[now]=y; } } void dfs2(int now,int topf){ top[now]=topf; if(!son[now])return; dfs2(son[now],topf); for(int i=head[now];i;i=nxt[i]){ int y=ver[i]; if(y==son[now]||y==father[now])continue; dfs2(y,y); } } int get_LCA(int x,int y){ while(top[x]!=top[y]){ if(deep[top[x]]<deep[top[y]])swap(x,y); x=father[top[x]]; } if(deep[x]>deep[y])swap(x,y); return x; } void turn(int now){ int a[_]={0},tt=0; while(now>0){ a[++tt]=now%2;now/=2; } for(int i=tt;i>=1;i--)cout<<a[i]; cout<<endl; } signed main(){ number=read();edge_n=read();root=1; for(int i=1;i<=edge_n;i++){ cx[i]=read(),cy[i]=read(); add(cx[i],cy[i]);add(cy[i],cx[i]); } for(int i=1;i<=number;i++) if(!dfn[i])Tarjan(i,0); memset(head,0,sizeof(head));memset(nxt,0,sizeof(nxt)); memset(ver,0,sizeof(ver));tot=0; for(int i=1;i<=edge_n;i++){ if(color[cx[i]]!=color[cy[i]]) add(color[cx[i]],color[cy[i]]),add(color[cy[i]],color[cx[i]]); } dfs1(root,0,0);dfs2(root,root); number_w=read(); for(int i=1;i<=number_w;i++){ int x=read(),y=read(),lca=get_LCA(color[x],color[y]); // cout<<color[x]<<" "<<color[y]<<" "<<lca<<" : "; turn(dis[color[x]]+dis[color[y]]-2*dis[lca]+1); } return 0; }