poj 1034 The dog task (二分匹配)

The dog task

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2559		Accepted: 1038		Special Judge

Description

Hunter Bob often walks with his dog Ralph. Bob walks with a constant speed and his route is a polygonal line (possibly self-intersecting) whose vertices are specified by N pairs of integers (Xi, Yi) ? their Cartesian coordinates. 
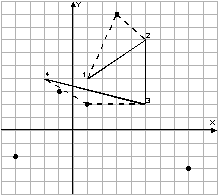
Ralph walks on his own way but always meets his master at the specified N points. The dog starts his journey simultaneously with Bob at the point (X1, Y1) and finishes it also simultaneously with Bob at the point (XN, YN). 
Ralph can travel at a speed that is up to two times greater than his master's speed. While Bob travels in a straight line from one point to another the cheerful dog seeks trees, bushes, hummocks and all other kinds of interesting places of the local landscape which are specified by M pairs of integers (Xj',Yj'). However, after leaving his master at the point (Xi, Yi) (where 1 <= i < N) the dog visits at most one interesting place before meeting his master again at the point (Xi+1, Yi+1). 
Your task is to find the dog's route, which meets the above requirements and allows him to visit the maximal possible number of interesting places. The answer should be presented as a polygonal line that represents Ralph's route. The vertices of this route should be all points (Xi, Yi) and the maximal number of interesting places (Xj',Yj'). The latter should be visited (i.e. listed in the route description) at most once. 
An example of Bob's route (solid line), a set of interesting places (dots) and one of the best Ralph's routes (dotted line) are presented in the following picture: 

Input

The first line of the input contains two integers N and M, separated by a space ( 2 <= N <= 100 ,0 <= M <=100 ). The second line contains N pairs of integers X1, Y1, ..., XN, YN, separated by spaces, that represent Bob's route. The third line contains M pairs of integers X1',Y1',...,XM',YM', separated by spaces, that represent interesting places. 
All points in the input file are different and their coordinates are integers not greater than 1000 by the absolute value. 

Output

The first line of the output should contain the single integer K ? the number of vertices of the best dog's route. The second line should contain K pairs of coordinates X1'',Y1'' , ...,Xk'',Yk'', separated by spaces, that represent this route. If there are several such routes, then you may write any of them.

Sample Input

4 5
1 4 5 7 5 2 -2 4
-4 -2 3 9 1 2 -1 3 8 -3

Sample Output

6
1 4 3 9 5 7 5 2 1 2 -2 4

Source

Northeastern Europe 1998

//204K    32MS    C++    1612B    2013-11-11 09:07:25 
/*
    
    题意：
        有n个点，Bob要按序逐个走过，它的狗的速度最大时他的两倍，每次在两点间他的狗都可以
    去浏览一个有趣的点并回到Bob身边，问他的狗最多可以浏览多少个有趣的点，并输出狗经过的点 
    
    二分匹配：
        Bob要走的点看成是二分中的一个集合，有趣的点看成是二分的另一集合，很明显构图时要符合
    有趣点到一条Bob必经路径两点的距离和 小于等于 2*该路径长度时，路径和该有趣的点联通，构好
    图后直接匈牙利模板 
     
*/
#include<stdio.h>
#include<string.h>
#include<math.h>
struct node{
    double x,y;
}p[105],q[105];
int g[105][105];
int match[105];
int vis[105];
int n,m;
double L(node a,node b) //求两点距离 
{
    return sqrt((a.y-b.y)*(a.y-b.y)+(a.x-b.x)*(a.x-b.x));
}
void build()
{
    memset(g,0,sizeof(g));
    for(int i=0;i<n-1;i++){
        double l=L(p[i],p[i+1]); 
        for(int j=0;j<m;j++)
            if(L(p[i],q[j])+L(p[i+1],q[j])<=2*l) //条件 
                g[i][j]=1;
    }
}
int dfs(int x)
{
    for(int i=0;i<m;i++){
        if(!vis[i] && g[x][i]){
            vis[i]=1;
            if(match[i]==-1 || dfs(match[i])){
                match[i]=x;
                return 1;
            }
        }
    }
    return 0;
}
void hungary()
{
    memset(match,-1,sizeof(match));
    int ret=0;
    for(int i=0;i<n-1;i++){
        memset(vis,0,sizeof(vis));
        if(dfs(i)) ret++;
    }
    printf("%d
",ret+n);
    int flag[105][2]={0}; //第二维保存的是必经点中哪个点后有有趣的点和该有趣的点的下标 
    for(int i=0;i<m;i++)
        if(match[i]!=-1){
            flag[match[i]][0]=1;
            flag[match[i]][1]=i;
        }
    for(int i=0;i<n-1;i++){ //输出 
        printf("%.0lf %.0lf ",p[i].x,p[i].y);
        if(flag[i][0]){
            printf("%.0lf %.0lf ",q[flag[i][1]].x,q[flag[i][1]].y);
        }
    }
    printf("%.0lf %.0lf
",p[n-1].x,p[n-1].y);
}
int main(void)
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        for(int i=0;i<n;i++)
            scanf("%lf%lf",&p[i].x,&p[i].y);
        for(int i=0;i<m;i++)
            scanf("%lf%lf",&q[i].x,&q[i].y);
        build();
        hungary();
    }
    return 0;
}