Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 48890 | Accepted: 10917 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
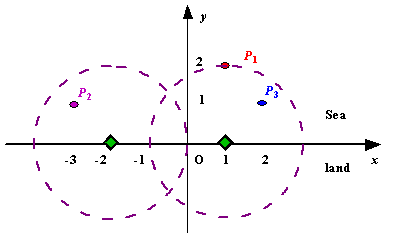
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
Source
给你n个点和雷达探测半径d,问在x轴上最少要放多少个雷达使雷达探测覆盖所有的点。
贪心思想:按x轴小到大排序,然后求得圆心,在判断过程中修正圆心位置,最后以O(n)求解。
//204K 16MS C++ 1223B 2014-04-27 09:22:25 #include<stdio.h> #include<stdlib.h> #include<math.h> struct node{ double x,y; }p[1005]; int cmp(const void*a,const void*b) { node *x=(node*)a; node *y=(node*)b; if(x->x!=y->x) return (x->x)>(y->x)?1:-1; return (x->y)>(y->y)?-1:1; } double dis(node a,node b) { return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } double getx(double d,node p0) { return p0.x+sqrt(d*d-p0.y*p0.y); } int main(void) { int n,k=1; int d0; while(scanf("%d%d",&n,&d0),n+d0) { double d=d0*1.0; int flag=0; for(int i=0;i<n;i++){ scanf("%lf%lf",&p[i].x,&p[i].y); if(p[i].y>d) flag=1; } printf("Case %d: ",k++); if(flag){ puts("-1");continue; } qsort(p,n,sizeof(p[0]),cmp); node q={getx(d,p[0]),0}; int cnt=1; for(int i=1;i<n;i++){ double temp=getx(d,p[i]); if(p[i].x<q.x && q.x>temp){ //开始少了这步.WA了几次 q.x=temp;continue; } if(dis(q,p[i])>d){ cnt++; q.x=getx(d,p[i]); } } printf("%d ",cnt); } return 0; }