1- The Child and Sequence
At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.
Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:
Print operation l, r. Picks should write down the value of .
Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).
Can you help Picks to perform the whole sequence of operations?
分析:
区间加和单点修改属于线段树的常规操作,但是区间取模的话,区间的和不能取模,所以要一个个地取模,但是真的去一个个遍历取模肯定会超时。
但是有这样的性质: 一个数x若比模数y小,则x不用取模;若x>=y,那么不管y是何值,也不管y会不会变动,x模到一个很小的数或者0的时间是log级别的(可以自己模拟试试)
所以我们维护区间的 sum(和)还有区间最大值 maxn ,如果maxn<y,那么不用模,否则就去递归取模.
代码
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 100005
#define MAXM
#define P
#define lson u<<1
#define rson u<<1|1
ll maxn[MAXN<<2],sum[MAXN<<2];
int n,m;
void pushup(int u){
sum[u]=sum[u<<1]+sum[u<<1|1];
maxn[u]=max(maxn[u<<1],maxn[u<<1|1]);
}
void build(int u,int l,int r){
if(l==r){
scanf("%d",&sum[u]);
maxn[u]=sum[u];
return;
}
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
}
ll Q(int u,int L,int R,int l,int r){
if(L>=l&&R<=r)return sum[u];
int mid=L+R>>1;
ll ret=0;
if(l<=mid)ret+=Q(lson,L,mid,l,r);
if(r>mid)ret+=Q(rson,mid+1,R,l,r);
return ret;
}
void upd1(int u,int L,int R,int l,int r,int x){
if(maxn[u]<x)return;
if(L==R){
sum[u]%=x;
maxn[u]%=x;
return;
}
int mid=L+R>>1;
if(l<=mid)upd1(lson,L,mid,l,r,x);
if(r>mid)upd1(rson,mid+1,R,l,r,x);
pushup(u);
}
void upd2(int u,int L,int R,int k,int x){
if(L==R){
sum[u]=x;
maxn[u]=x;
return;
}
int mid=L+R>>1;
if(k<=mid)upd2(lson,L,mid,k,x);
if(k>mid)upd2(rson,mid+1,R,k,x);
pushup(u);
}
int main(){
cin>>n>>m;
build(1,1,n);
while(m--){
int op;
scanf("%d",&op);
if(op==1){
int l,r;
scanf("%d%d",&l,&r);
printf("%lld
",Q(1,1,n,l,r));
}
else if(op==2){
int l,r,x;
scanf("%d%d%d",&l,&r,&x);
upd1(1,1,n,l,r,x);
}
else{
int k,x;
scanf("%d%d",&k,&x);
upd2(1,1,n,k,x);
}
}
return 0;
}
2- Transformation 利用线段树+lazytag
Yuanfang is puzzled with the question below:
There are n integers, a1, a2, …, an. The initial values of them are 0. There are four kinds of operations.
Operation 1: Add c to each number between ax and ay inclusive. In other words, do transformation ak<---ak+c, k = x,x+1,…,y.
Operation 2: Multiply c to each number between ax and ay inclusive. In other words, do transformation ak<---ak×c, k = x,x+1,…,y.
Operation 3: Change the numbers between ax and ay to c, inclusive. In other words, do transformation ak<---c, k = x,x+1,…,y.
Operation 4: Get the sum of p power among the numbers between ax and ay inclusive. In other words, get the result of axp+ax+1p+…+ay p.
Yuanfang has no idea of how to do it. So he wants to ask you to help him.
分析:tag有先后顺序,且他们会互相影响
代码
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 100005
#define MAXM
#define P
#define lson u<<1
#define rson u<<1|1
const ll mod=10007;
ll maxn[MAXN<<2],sum[MAXN<<2],sum2[MAXN<<2],sum3[MAXN<<2];
ll add[MAXN<<2],st[MAXN<<2],mul[MAXN<<2];
int n,m;
void pushup(int u){
sum[u]=sum[u<<1]+sum[u<<1|1];
sum[u]%=mod;
sum2[u]=(sum2[lson]+sum2[rson])%mod;
sum3[u]=(sum3[lson]+sum3[rson])%mod;
}
void build(int u,int l,int r){
add[u]=st[u]=0;
mul[u]=1;
if(l==r){
// cout<<u<<"&"<<l<<"&"<<r<<endl;
sum[u]=sum3[u]=sum2[u]=0;
return;
}
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
}
/*void pushdown(int u,int len){
if(st[u]){
st[lson]=st[rson]=st[u];
add[lson]=add[rson]=0;
mul[lson]=mul[rson]=1;
ll tmp=(st[u]*st[u])%mod*st[u]%mod;
sum[lson]=(len-len>>1)%mod*st[u]%mod;
sum[rson]=(len>>1)%mod*st[u]%mod;
sum2[lson]=((len - (len >>1))%mod) * ((st[u] * st[u])%mod)%mod;
sum2[rson]=((len >>1)%mod) * ((st[u] * st[u])%mod)%mod;
sum3[lson]=((len - (len >>1))%mod) * tmp%mod;
sum3[rson]=((len >> 1)%mod) * tmp%mod;
st[u]=0;
}
if(mul[u] != 1) {
mul[lson]=(mul[lson] * mul[u])%mod;
mul[rson]=(mul[rson] * mul[u])%mod;
if(add[lson])
add[lson]=(add[lson] * mul[u])%mod;
if(add[rson])
add[rson]=(add[rson] * mul[u])%mod;
ll tmp=(((mul[u] * mul[u])%mod * mul[u])%mod);
sum[lson]=(sum[lson] * mul[u])%mod;
sum[rson]=(sum[rson] * mul[u])%mod;
sum2[lson]=(sum2[lson]%mod) * ((mul[u] * mul[u])%mod)%mod;
sum2[rson]=(sum2[rson]%mod) * ((mul[u] * mul[u])%mod)%mod;
sum3[lson]=(sum3[lson]%mod) * tmp%mod;
sum3[rson]=(sum3[rson]%mod) * tmp%mod;
mul[u]=1;
}
if(add[u]) {
add[lson] += add[u];
add[rson] += add[u];
ll tmp=(add[u] * add[u]%mod) * add[u]%mod;
sum3[lson]=(sum3[lson] + (tmp * (len - (len >> 1))%mod) + 3 * add[u] * ((sum2[lson] + sum[lson] * add[u])%mod))%mod;
sum3[rson]=(sum3[rson] + (tmp * (len >> 1)%mod) + 3 * add[u] * ((sum2[rson] + sum[rson] * add[u])%mod))%mod;
sum2[lson]=(sum2[lson] + ((add[u] * add[u]%mod) * (len - (len >> 1))%mod) + (2 * sum[lson] * add[u]%mod))%mod;
sum2[rson]=(sum2[rson] + (((add[u] * add[u]%mod) * (len >> 1))%mod) + (2 * sum[rson] * add[u]%mod))%mod;
sum[lson]=(sum[lson] + (len - (len >> 1)) * add[u])%mod;
sum[rson]=(sum[rson] + (len >> 1) * add[u])%mod;
add[u]=0;
}
}
*/
void pushdown(int rt , int len)
{
if(st[rt]) {
st[rt << 1] = st[rt << 1 | 1] = st[rt];
add[rt << 1] = add[rt << 1 | 1] = 0; //注意这个也要下放
mul[rt << 1] = mul[rt << 1 | 1] = 1;
ll tmp = ((st[rt] * st[rt]) % mod) * st[rt] % mod;
sum[rt << 1] = ((len - (len >> 1)) % mod) * (st[rt] % mod) % mod;
sum[rt << 1 | 1] = ((len >> 1) % mod) * (st[rt] % mod) % mod;
sum2[rt << 1] = ((len - (len >> 1)) % mod) * ((st[rt] * st[rt]) % mod) % mod;
sum2[rt << 1 | 1] = ((len >> 1) % mod) * ((st[rt] * st[rt]) % mod) % mod;
sum3[rt << 1] = ((len - (len >> 1)) % mod) * tmp % mod;
sum3[rt << 1 | 1] = ((len >> 1) % mod) * tmp % mod;
st[rt] = 0;
}
if(mul[rt] != 1) {
mul[rt << 1] = (mul[rt << 1] * mul[rt]) % mod;
mul[rt << 1 | 1] = (mul[rt << 1 | 1] * mul[rt]) % mod;
if(add[rt << 1])
add[rt << 1] = (add[rt << 1] * mul[rt]) % mod;
if(add[rt << 1 | 1])
add[rt << 1 | 1] = (add[rt << 1 | 1] * mul[rt]) % mod;
ll tmp = (((mul[rt] * mul[rt]) % mod * mul[rt]) % mod);
sum[rt << 1] = (sum[rt << 1] * mul[rt]) % mod;
sum[rt << 1 | 1] = (sum[rt << 1 | 1] * mul[rt]) % mod;
sum2[rt << 1] = (sum2[rt << 1] % mod) * ((mul[rt] * mul[rt]) % mod) % mod;
sum2[rt << 1 | 1] = (sum2[rt << 1 | 1] % mod) * ((mul[rt] * mul[rt]) % mod) % mod;
sum3[rt << 1] = (sum3[rt << 1] % mod) * tmp % mod;
sum3[rt << 1 | 1] = (sum3[rt << 1 | 1] % mod) * tmp % mod;
mul[rt] = 1;
}
if(add[rt]) {
add[rt << 1] += add[rt];
add[rt << 1 | 1] += add[rt];
ll tmp = (add[rt] * add[rt] % mod) * add[rt] % mod;
sum3[rt << 1] = (sum3[rt << 1] + (tmp * (len - (len >> 1)) % mod) + 3 * add[rt] * ((sum2[rt << 1] + sum[rt << 1] * add[rt]) % mod)) % mod;
sum3[rt << 1 | 1] = (sum3[rt << 1 | 1] + (tmp * (len >> 1) % mod) + 3 * add[rt] * ((sum2[rt << 1 | 1] + sum[rt << 1 | 1] * add[rt]) % mod)) % mod;
sum2[rt << 1] = (sum2[rt << 1] + ((add[rt] * add[rt] % mod) * (len - (len >> 1)) % mod) + (2 * sum[rt << 1] * add[rt] % mod)) % mod;
sum2[rt << 1 | 1] = (sum2[rt << 1 | 1] + (((add[rt] * add[rt] % mod) * (len >> 1)) % mod) + (2 * sum[rt << 1 | 1] * add[rt] % mod)) % mod;
sum[rt << 1] = (sum[rt << 1] + (len - (len >> 1)) * add[rt]) % mod;
sum[rt << 1 | 1] = (sum[rt << 1 | 1] + (len >> 1) * add[rt]) % mod;
add[rt] = 0;
}
}
ll Q(int u,int L,int R,int l,int r,int p){
if(L>=l&&R<=r){
// cout<<L<<" "<<R<<"&"<<sum2[u]<<endl;
if(p==1)return sum[u]%mod;
if(p==2)return sum2[u]%mod;
return sum3[u]%mod;
}
pushdown(u,R-L+1);
int mid=L+R>>1;
ll ret=0;
if(l<=mid)ret+=Q(lson,L,mid,l,r,p);
ret%=mod;
if(r>mid)ret+=Q(rson,mid+1,R,l,r,p);
ret%=mod;
return ret;
}
void upd1(int u,int L,int R,int l,int r,int c,int p){
if(L>=l&&R<=r){
if(p==3){
st[u]=c;
add[u]=0;
mul[u]=1;
sum[u]=1LL*(R-L+1)*c%mod;
sum2[u]=1LL*(R-L+1)*c%mod*c%mod;
sum3[u]=sum2[u]*c%mod;
}
else if(p==2){
mul[u]=mul[u]*c%mod;
if(add[u])add[u]=add[u]*c%mod;
sum[u]=(sum[u]*c)%mod;
sum2[u]=(sum2[u]*c%mod*c)%mod;
sum3[u]=(sum3[u]*c%mod*c%mod*c)%mod;
}
else{
add[u]+=c;
ll tmp=c%mod*c%mod*c%mod*(R-L+1)%mod;
sum3[u]=(sum3[u]+tmp+3*c*(sum2[u]+c*sum[u]%mod))%mod;
sum2[u]=(sum2[u]+c*c%mod*(R-L+1)%mod+2*sum[u]*c)%mod;
sum[u]=(sum[u]+(R-L+1)*c)%mod;
// cout<<u<<"%%"<<sum[u]<<endl;
}
// cout<<L<<"->"<<R<<" "<<add[u]<<" "<<sum[u]<<endl;
return;
}
pushdown(u,R-L+1);
int mid=L+R>>1;
if(l<=mid)upd1(lson,L,mid,l,r,c,p);
if(r>mid)upd1(rson,mid+1,R,l,r,c,p);
pushup(u);
}
int main(){
// freopen("1.out","w",stdout);
while(cin>>n>>m){
if(n==0&&m==0)break;
build(1,1,n);
while(m--){
int op,a,b,c;
scanf("%d%d%d%d",&op,&a,&b,&c);
if(op==4){
printf("%lld
",Q(1,1,n,a,b,c));
}
else {
upd1(1,1,n,a,b,c,op);
}
// for(int i=1;i<=9;i++)cout<<i<<":"<<sum[i]<<" "<<sum2[i]<<" "<<add[i]<<endl;
}
}
return 0;
}
/*
5 5
3 3 5 7
1 2 4 4
4 1 5 2
2 2 5 8
4 3 5 3
0 0
*/
3-Codeforces Round #406 (Div. 2) D. Legacy
Rick and his co-workers have made a new radioactive formula and a lot of bad guys are after them. So Rick wants to give his legacy to Morty before bad guys catch them.
There are n planets in their universe numbered from 1 to n. Rick is in planet number s (the earth) and he doesn't know where Morty is. As we all know, Rick owns a portal gun. With this gun he can open one-way portal from a planet he is in to any other planet (including that planet). But there are limits on this gun because he's still using its free trial.
By default he can not open any portal by this gun. There are q plans in the website that sells these guns. Every time you purchase a plan you can only use it once but you can purchase it again if you want to use it more.
Plans on the website have three types:
With a plan of this type you can open a portal from planet v to planet u.
With a plan of this type you can open a portal from planet v to any planet with index in range [l, r].
With a plan of this type you can open a portal from any planet with index in range [l, r] to planet v.
Rick doesn't known where Morty is, but Unity is going to inform him and he wants to be prepared for when he finds and start his journey immediately. So for each planet (including earth itself) he wants to know the minimum amount of money he needs to get from earth to that planet.
分析:线段树优化建边
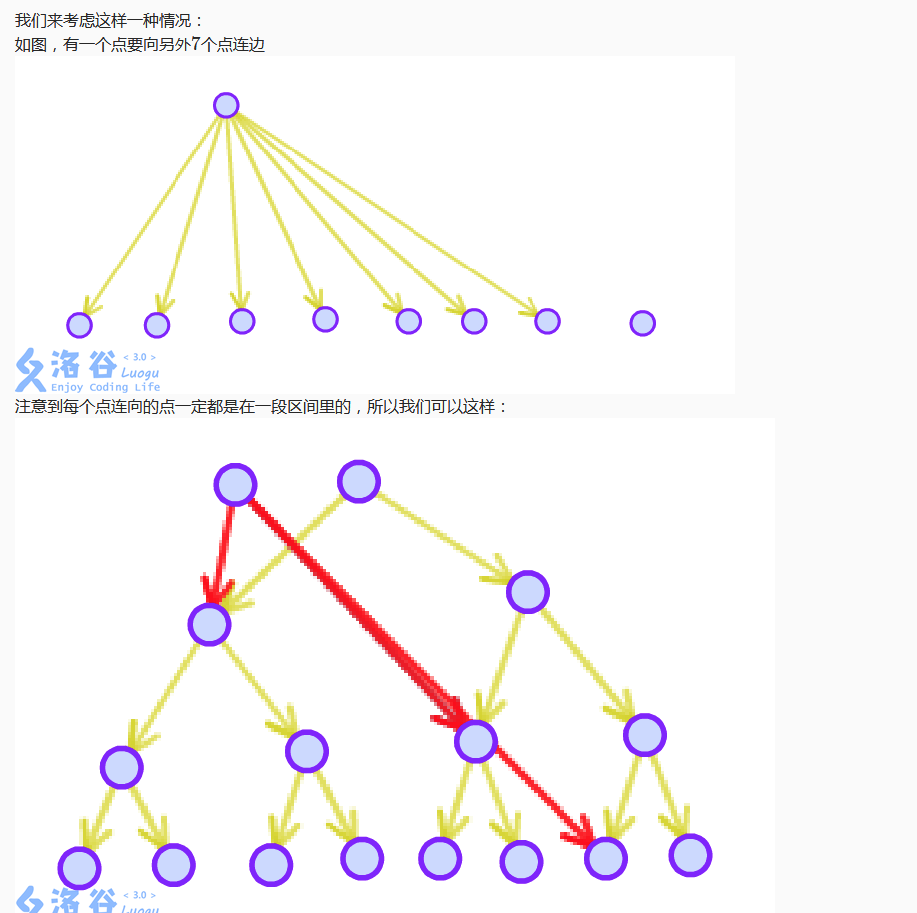
如果要让一个区间的点都向一个点连边,那么建树的时候就要建反边。注意初始建树正反都建一遍,而且叶子节点的id就等于它对应的点。
我的priotity_queue<pair<int,int>>里面忘记开longlong了,QAQ 调了好久
代码:
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 100005
#define MAXM
#define P
#define lson (u<<1)
#define rson (u<<1|1)
const ll inf=1e16;
int n,q,s,cnt;
int id1[MAXN<<2],id2[MAXN<<2];
vector<int>v1[MAXN*9],v2[MAXN*9];
ll dis[MAXN<<3];
bool In[MAXN<<3];
void add(int u,int v,int val){
v1[u].push_back(v);
v2[u].push_back(val);
}
void build1(int u,int l,int r){
int mid=l+r>>1;
id1[u]=++cnt;
if(l==r){
id1[u]=l;
return;
}
build1(u<<1,l,mid);
build1(u<<1|1,mid+1,r);
add(id1[u],id1[lson],0);
add(id1[u],id1[rson],0);
}
void build2(int u,int l,int r){
int mid=l+r>>1;
id2[u]=++cnt;
if(l==r){
id2[u]=l;
return;
}
build2(u<<1,l,mid);
build2(u<<1|1,mid+1,r);
add(id2[lson],id2[u],0);
add(id2[rson],id2[u],0);
}
void upd(int u,int L,int R,int v,int l,int r,int w,int op){
if(L>=l&&R<=r){
if(op==2)add(v,id1[u],w);
else add(id2[u],v,w);
return;
}
int mid=L+R>>1;
if(l<=mid)upd(lson,L,mid,v,l,r,w,op);
if(r>mid)upd(rson,mid+1,R,v,l,r,w,op);
}
void DJ(){
for(int i=1;i<=cnt;i++)dis[i]=inf;
priority_queue<pair<ll,int>>q;
dis[s] = 0;
q.push(make_pair(0,s));
while(!q.empty()){
int x = q.top().second;
q.pop();
if(In[x])continue;
In[x] = 1;
for(int i = 0; i<v1[x].size();i ++){
int y = v1[x][i];
ll z = v2[x][i];
if(dis[y] > dis[x] + z){
dis[y] = dis[x] + z;
q.push(make_pair(-dis[y], y));
}
}
}
}
int main(){
cin>>n>>q>>s;
cnt=n;
build1(1,1,n);
build2(1,1,n);
while(q--){
int op,v,u,w,l,r;
scanf("%d",&op);
if(op==1){
scanf("%d%d%d",&v,&u,&w);
add(v,u,w);
}
else{
scanf("%d%d%d%d",&v,&l,&r,&w);
upd(1,1,n,v,l,r,w,op);
}
}
DJ();
for(int i=1;i<=n;i++){
if(dis[i]==inf)printf("-1 ");
else printf("%lld ",dis[i]);
}
return 0;
}
4-Till I Collapse CF786C
Rick and Morty want to find MR. PBH and they can't do it alone. So they need of Mr. Meeseeks. They Have generated n Mr. Meeseeks, standing in a line numbered from 1 to n. Each of them has his own color. i-th Mr. Meeseeks' color is ai.
Rick and Morty are gathering their army and they want to divide Mr. Meeseeks into some squads. They don't want their squads to be too colorful, so each squad should have Mr. Meeseeks of at most k different colors. Also each squad should be a continuous subarray of Mr. Meeseeks in the line. Meaning that for each 1 ≤ i ≤ e ≤ j ≤ n, if Mr. Meeseeks number i and Mr. Meeseeks number j are in the same squad then Mr. Meeseeks number e should be in that same squad.
Also, each squad needs its own presidio, and building a presidio needs money, so they want the total number of squads to be minimized.
Rick and Morty haven't finalized the exact value of k, so in order to choose it, for each k between 1 and n (inclusive) need to know the minimum number of presidios needed.
分析:该题要求,让k=1~n,求每一个squads内颜色不超过k种的最少squads数。使用主席树记录每一种颜色出现的最后一个位置,然后从后往前,二分找到下一个位置。时间复杂度 n*log^2 ,因为是至少k种,所以到最后一次二分时,squads内可能没有k种。还有主席树空间最好开40倍,不然溢出到下一个数组了答案只会显示wa。主席树继承的时候记得把值也继承上。(而且在一个点多次修改的话root【i】要从root【i】继承噢。
代码:
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 100005
#define MAXM
#define P
int cnt,tr[MAXN*40],n,ls[MAXN*40],rs[MAXN*40],Last[MAXN*40],V[MAXN*40];
void build(int &p,int l,int r){
p=++cnt;
if(l==r)return;
int mid=l+r>>1;
build(ls[p],l,mid);
build(rs[p],mid+1,r);
}
void upd(int &p,int rec,int l,int r,int pos,int ad){
p=++cnt;
ls[p]=ls[rec];
rs[p]=rs[rec];
V[p]=V[rec];
if(l==r){
V[p]+=ad;
return;
}
int mid=l+r>>1;
if(pos>mid)upd(rs[p],rs[rec],mid+1,r,pos,ad);
else upd(ls[p],ls[rec],l,mid,pos,ad);
V[p]=V[ls[p]]+V[rs[p]];
}
int Q(int p,int l,int r,int s){
if(l==r&&V[p]==s)return l;
else if(l==r)return -1;
int mid=l+r>>1;
if(V[rs[p]]>=s) return Q(rs[p],mid+1,r,s);
return Q(ls[p],l,mid,s-V[rs[p]]);
}
int main(){
int n;
scanf("%d",&n);
build(tr[0],1,n);
for(int i=1,co;i<=n;i++){
scanf("%d",&co);
if(Last[co]!=0){
upd(tr[i],tr[i-1],1,n,Last[co],-1);
upd(tr[i],tr[i],1,n,i,1);
}
else
upd(tr[i],tr[i-1],1,n,i,1);
Last[co]=i;
}
for(int i=1;i<=n;i++){
int ans=0,ps=n,lastps=n;
do{
ps=Q(tr[ps],1,n,i+1);
++ans;
}while(ps>=1);
printf("%d ",ans);
}
return 0;
}
5-Kth number HDU2665
Give you a sequence and ask you the kth big number of a inteval.
分析:注意这个题意估计是chinglish,应该要求第k小的数.
代码:
#include<bits/stdc++.h>
#define N 100005
#define re(x) scanf("%d",&x);
using namespace std;
struct ee{
int num,id;
}e[N];
int Rank[N],Root[N],cnt,tot;
bool cp(ee a,ee b){
if(a.num!=b.num)
return a.num<b.num;
return a.id<b.id;
}
struct TREE{
int val,ls,rs;
TREE(){
val=0;
}
}tr[N*20];
void upd(int l,int r,int p,int &now,int last){//now是当前位置(我们会改变now从而建立newtree)
now=++tot;//!!!!there must be a tot!!
tr[now]=tr[last];
tr[now].val++;
if(l==r)return;
int mid=l+r>>1;
if(p<=mid)upd(l,mid,p,tr[now].ls,tr[last].ls);
else upd(mid+1,r,p,tr[now].rs,tr[last].rs);
}
int Q(int l,int r,int i,int j,int k){
if(l==r) return l;
int F=tr[tr[j].ls].val-tr[tr[i].ls].val;
int mid=l+r>>1;
if(k<=F)//!
return Q(l,mid,tr[i].ls,tr[j].ls,k);
else
return Q(mid+1,r,tr[i].rs,tr[j].rs,k-F);//F贡献完了
}
int main(){
int T;
cin>>T;
while(T--){
int n,m;
re(n);re(m);
memset(Root,0,sizeof(Root));
for(int i=0;i<=n*20;i++)tr[i].val=0;
tot=cnt=0;
for(int i=1;i<=n;i++){re(e[i].num);e[i].id=i;}
sort(e+1,e+1+n,cp);
for(int i=1;i<=n;i++)
Rank[e[i].id]=i;
for(int i=1;i<=n;i++){
Root[i]=Root[i-1];
upd(1,n,Rank[i],Root[i],Root[i-1]);
}
int u,v,k;
for(int i=1;i<=m;i++){
re(u);re(v);re(k);
printf("%d
",e[Q(1,n,Root[u-1],Root[v],k)].num);
}
}
return 0;
}
6-To the moon HDU4348
You‘ve been given N integers A[1], A[2],..., A[N]. On these integers, you need to implement the following operations:
- C l r d: Adding a constant d for every {Ai | l <= i <= r}, and increase the time stamp by 1, this is the only operation that will cause the time stamp >increase.
- Q l r: Querying the current sum of {Ai | l <= i <= r}.
- H l r t: Querying a history sum of {Ai | l <= i <= r} in time t.
- B t: Back to time t. And once you decide return to a past, you can never be access to a forward edition anymore.
.. N, M ≤ 105, |A[i]| ≤ 109, 1 ≤ l ≤ r ≤ N, |d| ≤ 104 .. the system start from time 0, and the first modification is in time 1, t ≥ 0, and won't introduce you to a future state.
分析:主席树题。注意主席树和线段树有点不一样,区间更新不能pushdown(你还没建好lson和rson呢)所以更新时一直更新沿途的结点,统计时,让沿途的结点加上自己的tag
代码:
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 100005
#define MAXM
#define P
int cnt,tr[MAXN*27],n,ls[MAXN*27],rs[MAXN*27];
ll V[MAXN*27],tag[MAXN*27];
void pushup(int p){
V[p]=V[ls[p]]+V[rs[p]];
}
void pushdown(int p,int len){
tag[ls[p]]+=tag[p];
tag[rs[p]]+=tag[p];
V[ls[p]]+=1ll*tag[p]*(len-(len>>1));
V[rs[p]]+=1ll*tag[p]*(len>>1);
tag[p]=0;
}
void build(int &p,int l,int r){
p=++cnt;
if(l==r){
scanf("%lld",&V[p]);
return;
}
int mid=l+r>>1;
build(ls[p],l,mid);
build(rs[p],mid+1,r);
pushup(p);
}
ll Q(int p,int L,int R,int l,int r){
// cout<<p<<"~~"<<L<<" "<<R<<"is"<<V[p]<<endl;
if(L>=l&&R<=r)return V[p];
int mid=L+R>>1;
ll ret=1ll*(min(r,R)-max(l,L)+1)*tag[p];
if(l<=mid)ret+=Q(ls[p],L,mid,l,r);
if(r>mid)ret+=Q(rs[p],mid+1,R,l,r);
return ret;
}
void upd(int &p,int rec,int L,int R,int l,int r,int d){
p=++cnt;
ls[p]=ls[rec];
rs[p]=rs[rec];
V[p]=V[rec];
tag[p]=tag[rec];
V[p]+=1ll*(min(r,R)-max(l,L)+1)*d;
int mid=L+R>>1;
if(L>=l&&R<=r){
tag[p]+=d;
return;
}
if(l<=mid)
upd(ls[p],ls[rec],L,mid,l,r,d);
if(r>mid)
upd(rs[p],rs[rec],mid+1,R,l,r,d);
}
int main(){
int n,m;
while(cin>>n>>m){
cnt=0;
memset(V,0,sizeof(V));
memset(tag,0,sizeof(tag));
build(tr[0],1,n);
int tnow=0;
while(m--){
char op;
cin>>op;
int l,r,d,t;
if (op=='Q')
{
scanf("%d%d",&l,&r);
printf("%lld
",Q(tr[tnow],1,n,l,r));
}
else if(op=='C'){
++tnow;
scanf("%d%d%d",&l,&r,&d);
upd(tr[tnow],tr[tnow-1],1,n,l,r,d);
}
else if(op=='H'){
scanf("%d%d%d",&l,&r,&t);
printf("%lld
",Q(tr[t],1,n,l,r));
}
else{
scanf("%d",&t);
tnow=t;
}
}
}
}
7-Just (h)-index HDU6278
The h-index of an author is the largest h where he has at least h papers with citations not less than h.
Bobo has published n papers with citations a1,a2,…,an respectively.
One day, he raises q questions. The i-th question is described by two integers li and ri, asking the h-index of Bobo if has only published papers with citations ali,ali+1,…,ari.
分析:看到这种区间,值域的题目就知道要用主席树。主席树可以求【L,R】区间内值为【low,high】的数的数量。此题n的范围是1e5,两个log可做,主席树+二分。
代码:
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 100005
#define MAXM
#define P
int cnt=0,ls[MAXN*30],rs[MAXN*30],V[MAXN*30],tr[MAXN*30],n;
void build(int &p,int l,int r){
p=++cnt;
V[p]=0;
if(l==r){
return;
}
int mid=l+r>>1;
build(ls[p],l,mid);
build(rs[p],mid+1,r);
}
void upd(int &p,int rec,int L,int R,int k){
p=++cnt;
V[p]=V[rec];
V[p]++;
ls[p]=ls[rec];
rs[p]=rs[rec];
if(L==R)return;
int mid=L+R>>1;
if(k<=mid)upd(ls[p],ls[rec],L,mid,k);
else upd(rs[p],rs[rec],mid+1,R,k);
}
int Q(int p,int rec,int L,int R,int down,int up)
{
if(L>=down&&R<=up){
// cout<<"p"<<p<<"rec"<<" "<<V[rec]-V[p]<<endl;
return -V[p]+V[rec];
}
int mid=L+R>>1,ret=0;
if(down<=mid)ret+=Q(ls[p],ls[rec],L,mid,down,up);
if(up>mid)ret+=Q(rs[p],rs[rec],mid+1,R,down,up);
return ret;
}
bool ok(int l,int r,int h){ ;
return Q(tr[l-1],tr[r],1,n,h,n)>=h;
}
int main(){
int q;
while(cin>>n>>q){
cnt=0;
build(tr[0],1,n);
for(int i=1,x;i<=n;i++){
scanf("%d",&x);
upd(tr[i],tr[i-1],1,n,x);
}
while(q--){
int l,r;
scanf("%d%d",&l,&r);
int L=1,R=n,ans=-1;
while(L<=R){
int mid=L+R>>1;
if(ok(l,r,mid))L=mid+1,ans=mid;
else
R=mid-1;
}
printf("%d
",ans);
}
}
return 0;
}
/*
5 3
1 5 3 2 1
1 3
2 4
1 5
5 1
1 2 3 4 5
1 5
*/
8-HDU 5919
Mr. Frog has an integer sequence of length n, which can be denoted as a1,a2,⋯,an There are m queries.
In the i-th query, you are given two integers li and ri. Consider the subsequence ali,ali+1,ali+2,⋯,ari.
We can denote the positions(the positions according to the original sequence) where an integer appears first in this subsequence as p(i)1,p(i)2,⋯,p(i)ki (in ascending order, i.e.,p(i)1<p(i)2<⋯<p(i)ki).
Note that ki is the number of different integers in this subsequence. You should output p(i)⌈ki2⌉for the i-th query.
分析:这道题目要看懂题意也不容易啊。。。就是给你一个区间,让你把这个区间的数去重,只留下在这个区间第一次出现的位置,然后输出中位数。要求在线做。
主席树倒着upd,在每一个root【i】都把原位置-1,i位置+1(注意主席树存的是位置而不是数值),然后查找时,就直接从root【L】查和二分统计。
代码:
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 200005
#define MAXM
#define P
int cnt=0,ls[MAXN*40],rs[MAXN*40],V[MAXN*40],tr[MAXN*40],n;
void build(int &p,int l,int r){
p=++cnt;
V[p]=0;
if(l==r){
return;
}
int mid=l+r>>1;
build(ls[p],l,mid);
build(rs[p],mid+1,r);
}
void upd(int &p,int rec,int L,int R,int k,int op){
p=++cnt;
V[p]=V[rec];
V[p]+=op;
ls[p]=ls[rec];
rs[p]=rs[rec];
// cout<<L<<"->"<<R<<" "<<V[p]<<endl;
if(L==R)return;
int mid=L+R>>1;
if(k<=mid)upd(ls[p],ls[rec],L,mid,k,op);
else upd(rs[p],rs[rec],mid+1,R,k,op);
}
int Q1(int p,int L,int R,int l,int r){
// cout<<L<<"&"<<R<<endl;
if(L>=l&&R<=r)return V[p];
int mid=L+R>>1,ret=0;
if(l<=mid)ret+=Q1(ls[p],L,mid,l,r);
if(r>mid)ret+=Q1(rs[p],mid+1,R,l,r);
// cout<<L<<"to"<<R<<" "<<ret<<endl;
return ret;
}
int Q(int p,int L,int R,int k)
{
// cout<<L<<"+"<<R<<endl;
if(L==R)return L;
int F=V[ls[p]];
int mid=L+R>>1;
if(F>=k)return Q(ls[p],L,mid,k);
else return Q(rs[p],mid+1,R,k-F);
}
int x[MAXN];
int main(){
int q,T;
cin>>T;
for(int cs=1;cs<=T;cs++){
map<int,int>occur;
cin>>n>>q;
cnt=0;
build(tr[n+1],1,n);
for(int i=1;i<=n;i++){
scanf("%d",&x[i]);
}
// cout<<"ok1"<<endl;
for(int i=n;i;i--){
if(occur[x[i]]){ //************************
upd(tr[i],tr[i+1],1,n,occur[x[i]],-1);
upd(tr[i],tr[i],1,n,i,1);
}
else upd(tr[i],tr[i+1],1,n,i,1);
occur[x[i]]=i;
}
int l,r,Preans=0;
printf("Case #%d:",cs);
while(q--){
scanf("%d%d",&l,&r);
int li=min((l+Preans) %n+1,(r+Preans) %n+1);
int ri=max((l+Preans) %n+1,(r+Preans) %n+1);
int k=Q1(tr[li],1,n,li,ri);
int pos=(k+1)>>1;
Preans=Q(tr[li],1,n,pos);
printf(" %d",Preans);
}
puts("");
}
return 0;
}
9- Cut and Stick CF1514D
Baby Ehab has a piece of Cut and Stick with an array a of length n written on it. He plans to grab a pair of scissors and do the following to it:
pick a range (l,r) and cut out every element al, al+1, ..., ar in this range;
stick some of the elements together in the same order they were in the array;
end up with multiple pieces, where every piece contains some of the elements and every element belongs to some piece.
More formally, he partitions the sequence al, al+1, ..., ar into subsequences. He thinks a partitioning is beautiful if for every piece (subsequence) it holds that, if it has length x, then no value occurs strictly more than ⌈x2⌉ times in it.He didn't pick a range yet, so he's wondering: for q ranges (l,r), what is the minimum number of pieces he needs to partition the elements al, al+1, ..., ar into so that the partitioning is beautiful.
A sequence b is a subsequence of an array a if b can be obtained from a by deleting some (possibly zero) elements. Note that it does not have to be contiguous.
分析 : 随机化求众数,然后x个非众数可以消化掉x+1个众数。剩下的众数自成一组。
代码:
#include <bits/stdc++.h>
using namespace std;
#define File(x) freopen("(x)","r",stdin)
#define pf printf
#define ull unsigned long long
#define db double
#define ll long long
#define MAXN 300005
#define MAXM
#define P
int n,q,a[MAXN];
vector<int>v[MAXN];
int main(){
srand(time(NULL));
cin>>n>>q;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
v[a[i]].push_back(i);
}
while(q--){
int l, r;
scanf("%d%d",&l,&r);
int Max=0,Id=-1;
for(int i=40;i;i--){
int id=rand()*rand()%(r-l+1)+l;
int mx=upper_bound(v[a[id]].begin(),v[a[id]].end(),r)-lower_bound(v[a[id]].begin(),v[a[id]].end(),l);
if(Max<mx){
Max=mx;
Id=id;
}
}
if(Max<=(r-l+1+1)/2)puts("1");
else
printf("%d
",Max-(r-l+1-Max));
}
return 0;
}