题目描述
现有一个n行m列的棋盘,一只马欲从棋盘的左上角跳到右下角。每一步它向右跳奇数列,且跳到本行或相邻行。跳越期间,马不能离开棋盘。例如,当n = 3, m = 10时,下图是一种可行的跳法。

试求跳法种数mod 30011。
输入
仅有一行,包含两个正整数n, m,表示棋盘的规模。
输出
仅有一行,包含一个整数,即跳法种数mod 30011。
样例输入
3 5
样例输出
10
题解
矩阵乘法
设 $f[i][j]$ 表示跳到 $(i,j)$ 的方案数,那么 $f[i][j]=sumlimits_{k=1}^{frac n2}f[i-2k+1][j-1]+f[i-2k+1][j]+f[i-2k+1][j+1]$。
那么我们维护两个前缀和:一个是与当前列相差为偶数的 $s1[i][j]$ 、一个是相差为奇数的 $s2[i][j]$ 。
当转移时如下图(红色为相差为偶数的 $s1$ ,蓝色为相差为奇数的 $s2$ ):
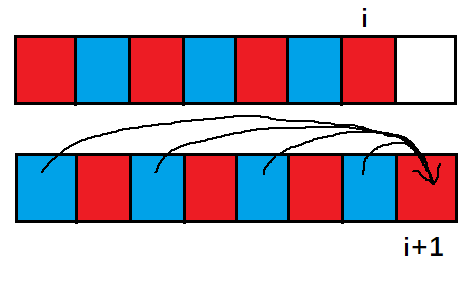
显然多出来的一个体现在 $s1[i+1]$ 上,与 $i+1$ 相差为奇数就与 $i$ 相差为偶数,由 $s1[i]$ 转移;而 $s2[i+1]$ 相对于 $s1[i]$ 没有改变。
于是就有 $s1[i+1][j]=s2[i][j]+s1[i][j-1]+s1[i][j]+s1[i][j+1] , s2[i+1][j]=s1[i][j]$
发现这个式子可以使用矩阵乘法来加速递推,因此直接矩乘即可。最后的答案就是前缀相减 $s1[m][n]-s2[m-1][n]$
时间复杂度 $O((2n)^3log m)$
#include <cstdio>
#include <cstring>
#include <algorithm>
#define mod 30011
using namespace std;
int n;
struct data
{
int v[105][105];
data() {memset(v , 0 , sizeof(v));}
int *operator[](int a) {return v[a];}
data operator*(data &a)
{
data ans;
int i , j , k;
for(i = 1 ; i <= n ; i ++ )
for(j = 1 ; j <= n ; j ++ )
for(k = 1 ; k <= n ; k ++ )
ans[i][j] = (ans[i][j] + v[i][k] * a[k][j]) % mod;
return ans;
}
}I , A , B;
data pow(data x , int y)
{
data ans;
int i;
for(i = 1 ; i <= n ; i ++ ) ans[i][i] = 1;
while(y)
{
if(y & 1) ans = ans * x;
x = x * x , y >>= 1;
}
return ans;
}
int main()
{
int m , i;
scanf("%d%d" , &n , &m);
for(i = 1 ; i <= n ; i ++ ) I[i][i] = I[i + n][i] = I[i][i + n] = 1;
for(i = 1 ; i < n ; i ++ ) I[i + 1][i] = I[i][i + 1] = 1;
n <<= 1 , A = pow(I , m - 2) , B = A * I;
printf("%d
" , (B[1][n >> 1] - A[1][n] + mod) % mod);
return 0;
}