到达型01背包问题,开个bool的dp数组.
此外还有滚动数组的用法.
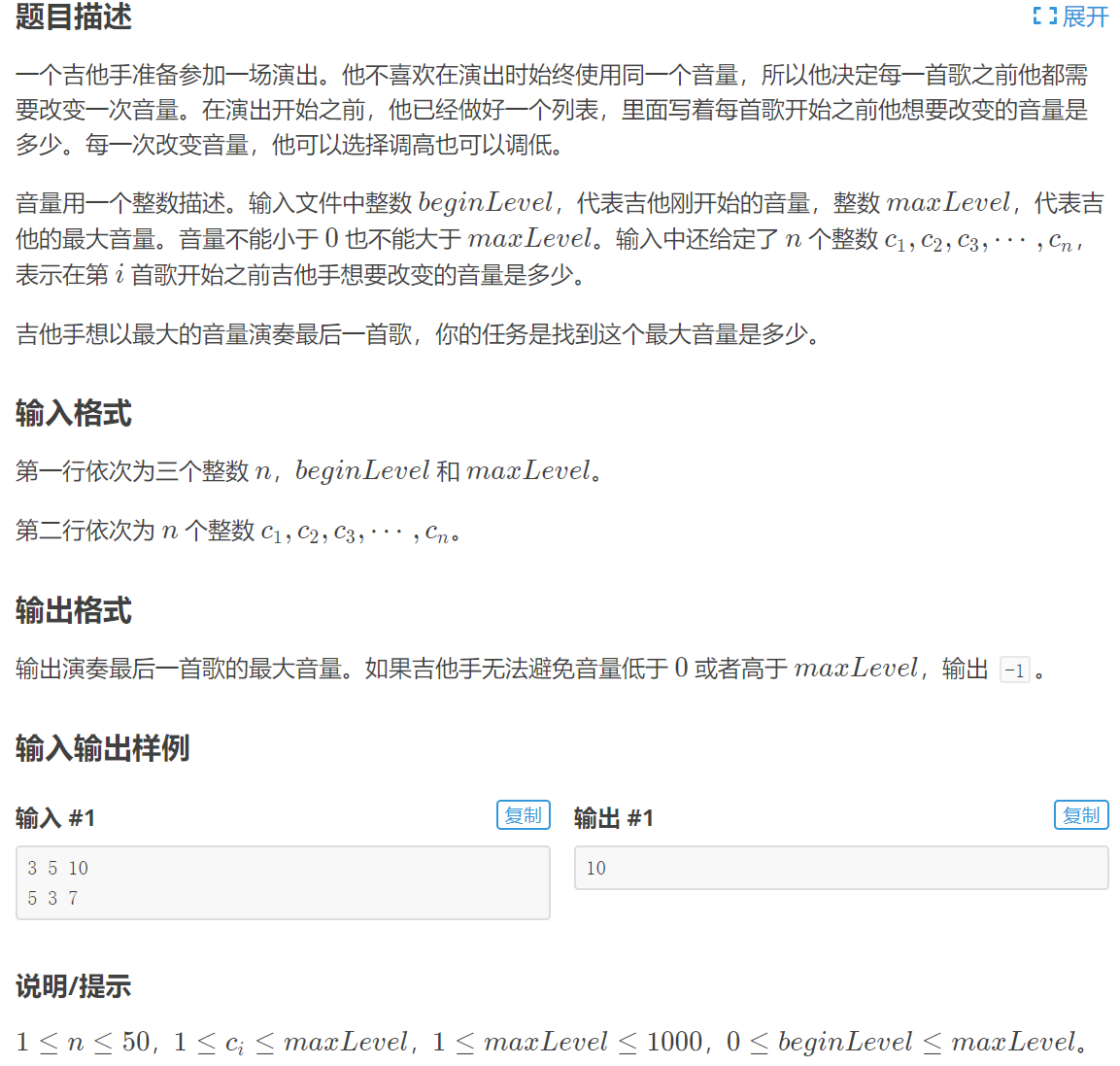
bool dp[i][j] 表示前i首歌能否到达j音量,则dp[0][beginLevel] = true.
如果上一首歌音量能够达到j + s[i] 或 j - s[i], 那么当前歌曲就可以达到j,注意处理越界情况.
尝试压维,变成dp[j],有如下代码:
#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; int n, be, ma, s[60]; bool dp[1010]; int main(){ cin >> n >> be >> ma; for(int i = 0; i < n; i++) cin >> s[i]; dp[be] = true; for(int i = 0; i < n; i++) for(int j = ma; j >= 0; j--) if(j - s[i] >= 0) if(j + s[i] <= ma) dp[j] = dp[j - s[i]] || dp[j + s[i]]; else dp[j] = dp[j - s[i]]; else // j - s[i] < 0 if(j + s[i] <= ma) dp[j] = dp[j + s[i]]; else dp[j] = false; return 0; }
调试几下发现错得一塌糊涂.这里面的问题在于涉及到dp[j + s[i]],由于数组的覆盖问题,j + s[i]总是为已经更新的当前歌曲(从i更新到i + 1)的状态,这是个错误.
为了避免这种干扰,来一招滚动数组轻松解决问题:
#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; int n, be, ma, s[60]; bool dp[2][1010]; int main() { cin >> n >> be >> ma; for (int i = 0; i < n; i++) cin >> s[i]; dp[0][be] = true; for (int i = 0; i < n; i++) for (int j = ma; j >= 0; j--) if (j - s[i] >= 0) if (j + s[i] <= ma) dp[(i + 1) & 1][j] = dp[i & 1][j - s[i]] || dp[i & 1][j + s[i]]; else dp[(i + 1) & 1][j] = dp[i & 1][j - s[i]]; else // j - s[i] < 0 if (j + s[i] <= ma) dp[(i + 1) & 1][j] = dp[i & 1][j + s[i]]; else dp[(i + 1) & 1][j] = false; for(int i = ma; i >= 0; i--) if(dp[n & 1][i]){ cout << i << endl; return 0; } puts("-1"); return 0; }
这里 按位与 "&" 用以判断奇偶数.
所以,虽然书上说开bool的dp经常会很浪费,但只要能够解决问题的时候不要思考受限,开它.