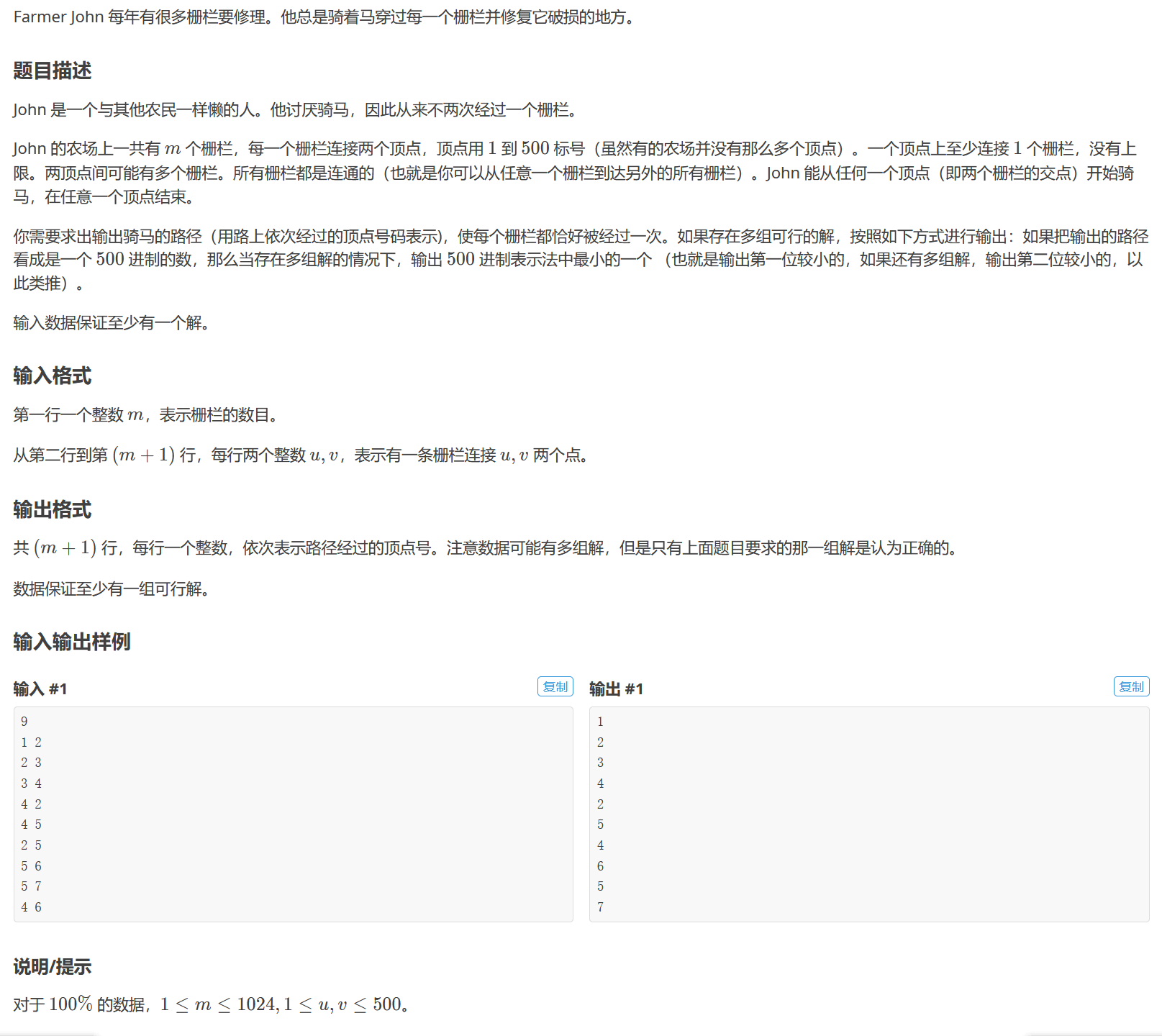
欧拉路径是这样的一条路径:它从一个点出发,可以将所有的边不重复地遍历一次,并在某一个点终止.
简单地说就是一笔画.
本文不讨论欧拉回路,即起点和终点相同的欧拉路径.
只采用Hierholzer算法,介绍及证明参考此处.
一.无向图欧拉路径的点路径
所谓点路径指的是按这个路径的顺序输出遍历的点.
这是无向有环图,并且是联通的,已知图存在欧拉路径,求解之.分两步进行:
1.求出起点
观察样例图
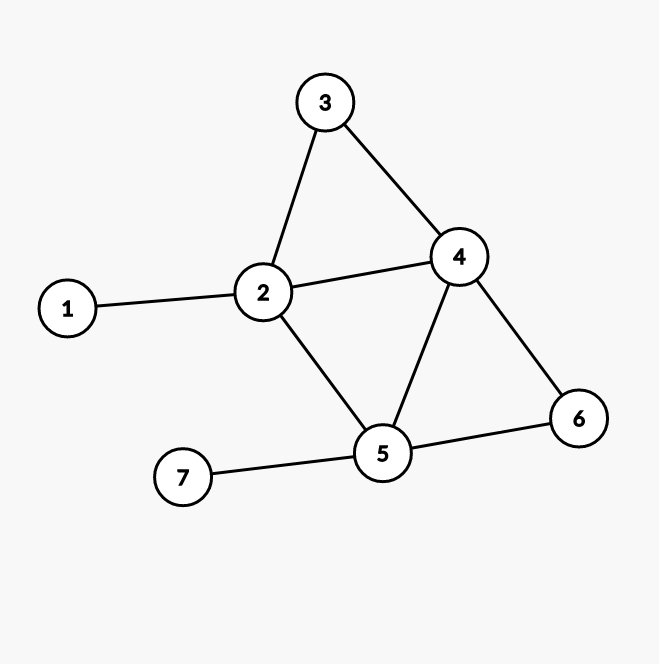
发现只有1,7,节点的度为奇数,而这1,7中就必然有一个是起点,且另一个是终点.
如果了解七桥问题,这是显然的.还可以推出,奇数度的节点数量超过两个或者只有一个时一定无解.
不存在奇数度的节点时,也一定有解,这时起点和终点为同一个点.
因此先要(按字典序一次)尝试查找度为奇数的节点,若找到即设为起点,因为题面保证有解.若没找到,则设1为起点.
2.递归求解
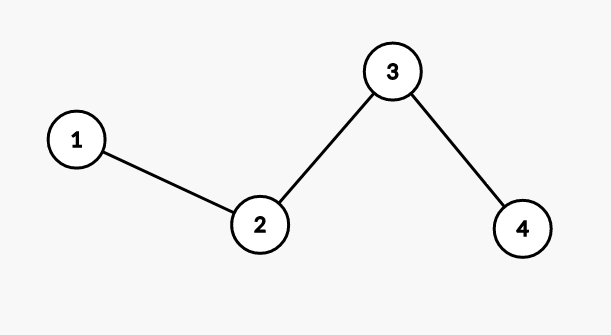
这张图的解是1-2-3-4.现在把它复杂化.
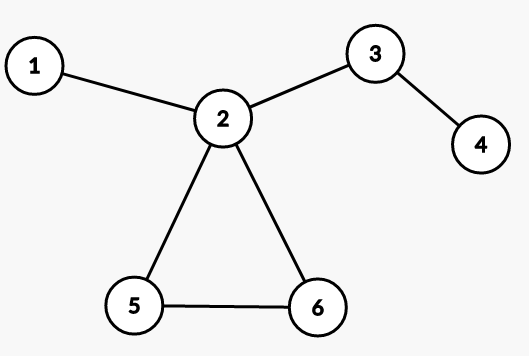
这张图的解是1-(2-5-6-2-)3-4,括号内是一个局部的欧拉路径.在保证有解的情况下,我猜想可以通过有限次的"复杂化"操作来构建任意一个图,所以是递归求解.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <stack> using namespace std; stack<int> ans; int s[1030][1030], deg[1030]; int n, m; void dfs(int x) { for (int i = 1; i <= n; i++) if (s[x][i]) { s[x][i]--; s[i][x]--; dfs(i); } ans.push(x); } int main() { cin >> m; int x, y; for (int i = 1; i <= m; i++) { cin >> x >> y; n = max({x, y, n}); s[x][y]++, s[y][x]++; deg[x]++, deg[y]++; } int head = 1; for (int i = 1; i <= n; i++) if (deg[i] & 1) { head = i; break; } dfs(head); while (!ans.empty()) { cout << ans.top() << endl; ans.pop(); } return 0; }
想要理解为什么用栈处理答案序列或者递归求解的证明可以看看开头的参考链接.
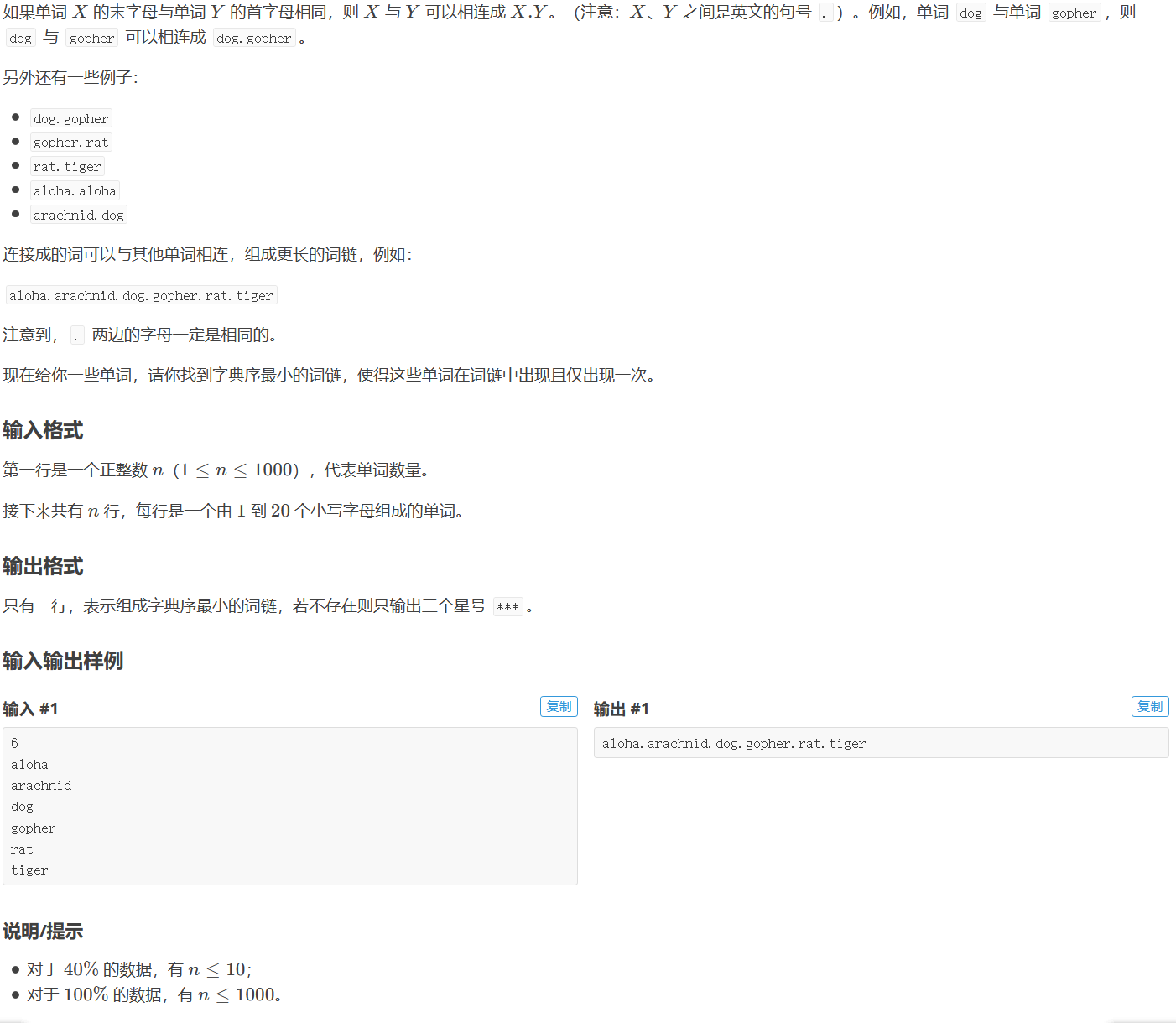
二.有向图欧拉路径的边路径
这道题目至少有两种做法,其一是把每个单词看作一个节点,求出一条不重复地遍历所有节点的路径,这是哈密顿路径,这里不讨论.
而如果把给出的每个单词视为从其开头字母指向末尾字母的一条路径,就需要求出所构成的图的欧拉回路,其中节点是a~z中的部分或全部.
这是有向有环图,并且需要先判断是否存在欧拉路径.对于无向图只需要统计度为奇数的节点数量,但有向图不能这么做.
1.判断是否联通
欧拉路径存在要求图必须联通,使用并查集处理,注意并查集的写法要考虑图的有向性.
2.判断是否存在欧拉路径
无向图的节点只有一个度,有向图有出度和入度.
对于任意一个非起点终点的节点,其入度显然必须等于出度.对于起点,入度必须比出度小1或者相等,对于终点,入度必须比出度大1或者相等.起点和终点的后者情况必须同时发生.
在此基础上就可以判断解的存在性并且求出起点了,并不需要关心终点的位置.
3.递归求解
仍然使用一个栈记录答案.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <stack> #include <vector> using namespace std; vector<pair<int, int> > G; stack<string> ans; string s[1010]; int n, ru[26], chu[26], fa[26]; bool used[1010], is[1010]; int odd, head; int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); } bool good() { for (int i = 0; i < 26; i++) fa[i] = i; for (int i = 0; i < G.size(); i++) { int a = G[i].first, b = G[i].second; int faa = find(a), fab = find(b); if (faa != fab) fa[faa] = fab; } int ct = 0; for (int i = 0; i < 26; i++) if (is[i] && fa[i] == i) ct++; if (ct != 1) return false; for (int i = 0; i < 26; i++) if (abs(chu[i] - ru[i]) >= 1) { odd++; if (abs(chu[i] - ru[i]) > 1) { cout << "***"; return 0; } else if (chu[i] - ru[i] == 1 && !head) head = i; } if (odd != 0 && odd != 2) return false; return true; } void dfs(int cur) { for (int i = 1; i <= n; i++) if (s[i][0] - 'a' == cur && !used[i]) { used[i] = true; dfs(s[i][s[i].length() - 1] - 'a'); ans.push(s[i]); } } int main() { cin >> n; for (int i = 1; i <= n; i++) cin >> s[i]; sort(s + 1, s + 1 + n); for (int i = 1; i <= n; i++) { int a = s[i][0] - 'a', b = s[i][s[i].length() - 1] - 'a'; is[a] = is[b] = true; G.push_back(make_pair(a, b)); G.push_back(make_pair(b, a)); ru[b]++, chu[a]++; } if (!good()) { cout << "***"; return 0; } else if (odd == 2) dfs(head); else for (int i = 0; i < 26; i++) if (is[i]) { dfs(i); if (ans.size() == n) break; } while (!ans.empty()) { cout << ans.top(); ans.pop(); if (!ans.empty()) cout << '.'; } cout << endl; return 0; }