[模板]最小生成树 Kruskal Prim

(这是一张边已经给出的无向图,不能自行加边,只能在当前的边中选择一些来求最小生成树.)

最小生成树:

定义:

给定一张边带权的无向图G=(V,E)，n = |V,m=|E|。由V中全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树。边的权值之和最小的生成树被称为无向图G的最小生成树（Minimum Spanning Tree,MST)。　　　　---<<指南>>

最小生成树一般只谈两种算法:Kruskal与Prim.

Kruskal模板O(|E|log|E|):

详细来说，Kruskal算法的流程如下:

 1.建立并查集，每个点各自构成一个集合。

 2.把所有边按照权值从小到大排序，依次扫描每条边(x,y,z)。

3.若x,y属于同一集合（连通)，则忽略这条边，继续扫描下一条。

4.否则，合并x,y所在的集合，并把z累加到答案中。

5.所有边扫描完成后，第4步中处理过的边就构成最小生成树。

时间复杂度为O(mlogm)。

　　　　　　　　　　　　　　　　　　　　　　--<<指南>>

书上这样的说法已经足够清晰了,不作证明,这里就放一些我自己写的实现供参考.

可以看出来模板性很强,不过题意可以变化多端,处理起来也有些变式,例如:

变式:

P2872 [USACO07DEC]Building Roads S

已经给定了必须选择的一些边,需要再自行添加一些边来求最小生成树.换句话说,在已经确定了一些边的完全图中求最小生成树.

而自行添加的边的选取范围即任意两点间构成的边的集合,即共有N²/2条边.

对于必须选择的边,应当先合并两端点的集合,之后穷举所有边并升序排列等执行Kruskal的流程.

P1396 营救

求最大值的最小情况,很容易想到用二分答案,这是一种可行的做法.

联想到Kruskal具有一些性质:

1.总是按权的升序处理边,

2.处理过程中的任意时刻,都是在用最小的代价来"生成"最大的(无更大的)"连通".

这意味着处理完某条边后,s与t将从不连通变为连通且保持此状态,并且此时的代价即为最小,因为任意时刻图上的边都构成当前的(若干个)最小生成树.

可以想到,进行Kruskal流程,一旦发现s与t变得连通了即可跳出,当前边的权值即为答案.

可以描述为:求"(最大边权值)最小(的)"生成树,使得s与t连通.

P1991 无线通讯网

在可以使得若干边无条件免费的情况下求完全图的最小生成树.

有x台卫星电话,意味着可以让最小生成树中权最大的x-1条边免费.

如果求最大生成树,只需要把升序排列改为降序排列边.

见此题.

进一步理解最小生成树:

罗列一下我自己感觉到的性质:

(以下均指完全图的最小生成树,由于边太多就不画出原完全图的边了)

(假设先移除完全图的所有边再加边计算生成树)

　　1. Kruskal执行过程中的任意时刻,图中的每个连通块的边都是其最小生成树的边.(这是显然的)

　　2.移除一张完全图的最小生成树中的任意边,产生的新连通块的边仍然是其最小生成树的边.

感受一下这张图中的最小生成树(不具有全体代表性,属于比较简单的情况):

权即为图中的长度.

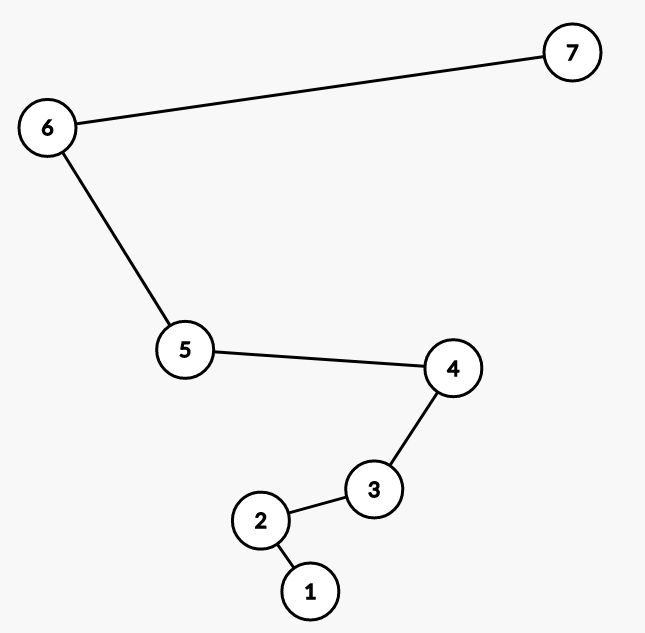
严格的证明,不会.但是基于Kruskal的贪心原理可以粗略地验证一下性质2的正确性:

对于一个完整的最小生成树,由于树的性质,每当移除其中的一条边,一定会把含有这条边的连通块分割为两个连通块.

(还可以知道,产生的两个连通块之间的点间的最短边即为这条边)

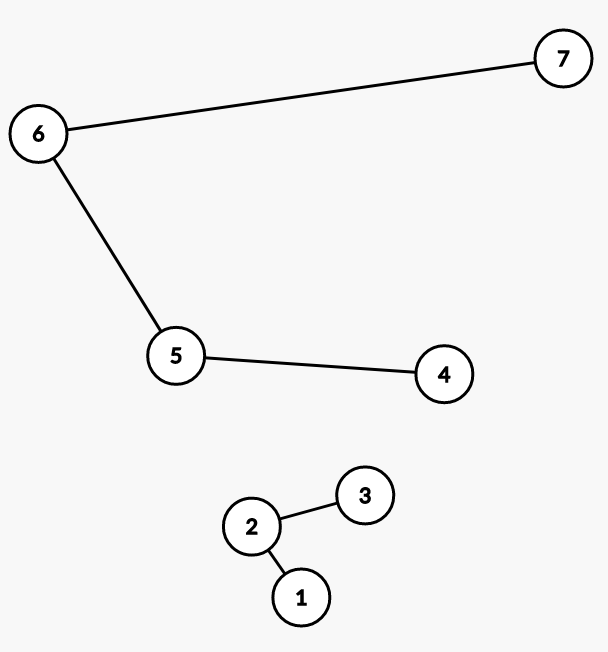
现在对其中任意一个连通块再进行Kruskal算法求其最小生成树,会发现这个过程与最初的连通块求取过程的一部分完全相同,仍然是从小权边到大权边连接.

现在看这道题:P4047 [JSOI2010]部落划分

靠得最近的两部落离得最远.(现在发现这种说法除了可能用二分,还可以用最小生成树)

上面提到,在最小生成树中移除一条边会使连通块数量加一,如果在完整的生成树的n-1条边中移除k-1条边,将会使得连通块数量从1增加到k,并且移除的边即为这些连通块之间的最短边.

根据题意,希望让部落的距离(定义为距离最近的两点的距离)尽可能大,那么不停地移除权最大的边即可.

这意味着只需要在连边时控制连到第n-k条时break,放弃此边并输出其权即可.

---

Prim模板O(N²):

Prim与Kruskal相对地,处理的对象是点.

设置两个集合,一个集合中为所有已经加入最小生成树的点,另一个中为未加入点.在每一轮操作中,O(N)遍历所有未加入的点,寻找其中与已有生成树距离最小者并将其加入生成树.如此进行N-1轮后所有点便加入了最小生成树.

其中,与最小生成树距离最近的点 定义为在两集合中各取一点使所得两点间距离最小,此定义即为未加入点集中所取的点.

实现方法如下,Prim模板的写法具有技巧性:

// used[i]的真假性相同者处于同一集合,故有两个集合
　　for (int i = 1; i < n; i++) {
        int x = 0;
        for (int j = 1; j <= n; j++)
            if (!used[j] && (x == 0 || dist[j] < dist[x])) x = j;
        used[x] = true;
        for(int k = 1; k <= n; k++)
            if(!used[k]) dist[k] = min(dist[k], calc(x, k));
    }
// dist[i](i>=2)即为点i加入最小生成树时所新建的边长度
// 因此最小生成树边长之和为dist[2]+...+dist[n]

前面的题目中,当出现完全图时若使用Kruskal往往需要先存储N²数量的边,这在空间复杂度上相对于Prim显示出了劣势.

　　Prim算法的时间复杂度为O(N²)，可以用二叉堆优化到 O(MlogN)。但用二叉堆优化不如直接使用 Kruskal算法更加方便。因此，Prim主要用于稠密图，尤其是完全图的最小生成树的求解。　　　　　　　　　　　　　　　　------<<指南>>

P1265 公路修建

使用Kruskal的尝试以MLE告终,而使用Prim可以避免存储O(N²)复杂度的数据.

注意题中"每个“城市联盟”将被看作一个城市，发挥一个城市的作用"可以视为每当一个节点加入了最小生成树时,下一步是找到与整个最小生成树最近的节点.

并且对于成环的情况:

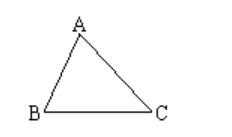
 A城市联盟会申请AB,C城市联盟会申请AC,但B城市联盟并不会申请BC,成环情况只可能在等边三角形时出现,而最小生成树算法本身就可以完全符合题意地处理这种情况.因此可以无视规则2.

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

struct P {
    int x, y;
} p[5010];
int n;
double dist[5010];
bool used[5010];

double calc(int u, int v) {
    long long dx = p[u].x - p[v].x, dy = p[u].y - p[v].y;
    return sqrt(dx * dx + dy * dy);
}
inline int read() {
    char ch = getchar();
    int x = 0, f = 1;
    while (ch > '9' || ch < '0') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int main() {
    // freopen("in.txt", "r", stdin);
    n = read();
    for (int i = 1; i <= n; i++) p[i].x = read(), p[i].y = read();
    fill(dist + 1, dist + n + 1, 1e9);
    dist[1] = 0;

    for (int i = 1; i < n; i++) {
        int x = 0;
        for (int j = 1; j <= n; j++)
            if (!used[j] && (x == 0 || dist[j] < dist[x])) x = j;
        used[x] = true;
        for(int k = 1; k <= n; k++)
            if(!used[k]) dist[k] = min(dist[k], calc(x, k));
    }

    double ans = 0;
    for(int i = 2; i <= n; i++) ans += dist[i];
    printf("%.2f
", ans);

    return 0;
}