线段树利用分治思想在区间上统计信息.
一颗线段树有着如下的结构:
1.线段树的每一个节点表示一段区间,保存着这段区间的左端点l,右端点r,以及该段区间的某些信息(如最值,和).
2.作为二叉树,对于每一个非叶节点,若其代表了区间[l,r],则其左儿子代表区间[l,mid],右儿子代表区间[mid+1,r](其中mid=⌊(l+r)/2⌋).
显然,线段树的根节点代表整个统计范围[1,n].
3.对于每一个叶节点,其代表的区间长度为1.
直观感受一下:(图-<<指南>>)
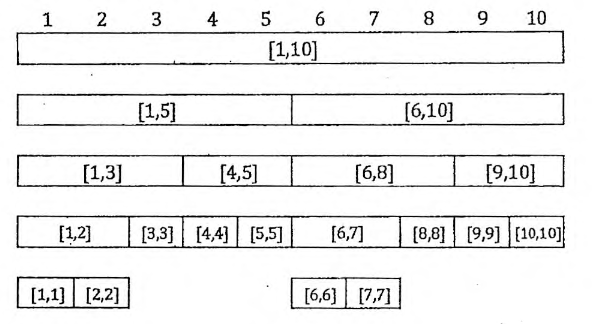
会发现,对于建立在区间[1,N]上的线段树,如果把最后一层补全会使该层有N~2N-1(不确定具体值,但一定是O(N))个节点,而对于这样的一颗二叉树,其高度为O(logN).
由此可知这个二叉树中会有O(N)个节点,实践中往往需要4*N的空间来存储才能保证足够.
基于二叉树结构,线段树可以方便地上下传递,整合信息,这里的信息必须是具有"结合律"的.
线段树分为两大类:
①单点修改+区间查询型
这种线段树支持的操作有:
1.建树O(N)
利用数组存储一颗二叉树,回忆一下手写堆是怎么做的:
对于节点p,其左儿子表示为p*2,右儿子表示为p*2+1.
struct ST{ // Segment Tree int l, r, big; }t[4 * N + 10]; int a[N + 10]; // 需要统计的数据区间 void build(int p, int l, int r){ t[p].l = l, t[p].r = r; if(l == r){ t[p].big = a[l]; return; } int mid = t[p].l + t[p].r >> 1; build(p * 2, l, mid), build(p * 2 + 1, mid + 1, r); // 下面维护所需的区间信息, 这里以区间最大值为例 t[p].big = max(t[p * 2].big, t[p * 2 + 1].big); }
// 调用一次build(1,1,n)即可建树
观察这个build,会发现它对时间是零浪费的(递归的下一个节点总是未遍历过的),因此时间复杂度为O(N).
此后,便可以用t[p]表示线段树的p号节点并访问其区间信息.
2.单点修改O(logN)
(以维护区间最大值为例)
假设现在有如下线段树(圆圈表示节点,其中的数字表示该节点代表的区间元素的最大值):
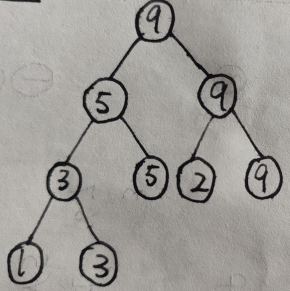
现在需要把最左下角节点(因为是叶节点,它对应原始数据中的一个元素)的数据改为10,会发现需要依次更新其父节点"③⑤⑨"为"⑩".
这个过程花费O(logN)时间.
不过需要先从根节点出发,找到需要修改的位置后再执行上述操作,这个过程也是O(logN)的.
void change(int p, int x, int v){ if(t[p].l == t[p].r){ t[p].big = v; return; } int mid = t[p].l + t[p].r >> 1; if(x <= mid) change(p * 2, x, v); else change(p * 2 + 1, x, v); t[p].big = max(t[p * 2].big, t[p * 2 + 1].big); }
// 调用change(1, x, v)将位于原始数据区间中位置为x的线段树节点信息更改为v
3.区间查询O(logN)
(仍是区间最大值)
想要获取给定区间[l,r]的信息,大多数情况下不存在某个线段树节点刚好存储着[l,r]的信息,因此需要整合多个节点的信息.
由于线段树的二分性质,总是可以用若干个节点不重不漏地表示范围内的任意区间.只需要进行如下操作:
检查区间[a,b]: 若被[l,r]包含,直接返回此区间(节点)的信息. 若与[l,r]不沾边,舍弃.(对于求区间最大值来说,实现方法是返回一个极小的值) 否则,把它从中间一刀两断为[a,mid],[mid+1,b]: 若mid>=l,那么递归地检查区间[a,mid]并整合信息. 若mid<r,那么递归地检查区间[mid+1,r]并整合信息. 返回整合后的信息.
这样的分治花费O(logN),递归终点总是检查区间被[l,r]包含的情况.
对于不同的区间信息,这里的整合有不同的方式,这里是查询区间最大值的实现,其中舍弃区间通过返回0实现:
int ask(int p, int l, int r){ if(t[p].r <= r && t[p].l >= l) return t[p].big; int ret = 0, mid = t[p].l + t[p].r >> 1; if(mid >= l) ret = max(ret, ask(p * 2, l, r)); if(mid < r) ret = max(ret, ask(p * 2 + 1, l, r)); return ret; }
// 调用ask(1, l, r)以查询区间[l, r]的最大值
现在就可以构造出一颗支持单点修改,查询区间最大值的线段树了,这里是模板题:

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; struct ST{ int l, r, big; }t[800010]; int n, m, a[200010]; void build(int p, int l, int r){ t[p].l = l, t[p].r = r; if(l == r){ t[p].big = a[l]; return; } int mid = t[p].l + t[p].r >> 1; build(p * 2, l, mid), build(p * 2 + 1, mid + 1, r); t[p].big = max(t[p * 2].big, t[p * 2 + 1].big); } void change(int p, int x, int v){ if(t[p].l == t[p].r){ t[p].big = v; return; } int mid = t[p].l + t[p].r >> 1; if(x <= mid) change(p * 2, x, v); else change(p * 2 + 1, x, v); t[p].big = max(t[p * 2].big, t[p * 2 + 1].big); } int ask(int p, int l, int r){ if(t[p].r <= r && t[p].l >= l) return t[p].big; int ret = 0, mid = t[p].l + t[p].r >> 1; if(mid >= l) ret = max(ret, ask(p * 2, l, r)); if(mid < r) ret = max(ret, ask(p * 2 + 1, l, r)); return ret; } void solve(){ for(int i = 1; i <= n; i++) scanf("%d", a + i); build(1, 1, n); while(m--){ char ch; int x, y; cin >> ch; scanf("%d%d", &x, &y); if(ch == 'Q') printf("%d ", ask(1, x, y)); else change(1, x, y); } } int main(){ while(scanf("%d%d", &n, &m) != EOF) solve(); return 0; }
在这个模板的基础上,对线段树的每种操作都稍加修改可以得到支持单点修改,查询区间和的线段树,总共只改了不到十行.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <string> using namespace std; struct ST { int l, r, sum; } t[200010]; int n, a[50010]; void build(int p, int l, int r) { t[p].l = l, t[p].r = r; if (l == r) { t[p].sum = a[l]; return; } int mid = l + r >> 1; build(p * 2, l, mid), build(p * 2 + 1, mid + 1, r); t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum; } void change(int p, int x, int v) { if (t[p].l == t[p].r) { t[p].sum += v; return; } int mid = t[p].l + t[p].r >> 1; if (x <= mid) change(p * 2, x, v); else change(p * 2 + 1, x, v); t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum; } int ask(int p, int l, int r) { if (l <= t[p].l && r >= t[p].r) return t[p].sum; int ret = 0; int mid = t[p].l + t[p].r >> 1; if (mid >= l) ret += ask(p * 2, l, r); if (mid < r) ret += ask(p * 2 + 1, l, r); return ret; } void solve() { string s; scanf("%d", &n); if (n == 0) { cin >> s; return; } for (int i = 1; i <= n; i++) scanf("%d", a + i); for (int i = 1; i <= n * 4; i++) t[i].l = t[i].r = t[i].sum = 0; build(1, 1, n); while (cin >> s && s[0] != 'E') { int x, y; scanf("%d%d", &x, &y); if (s[0] == 'Q') printf("%d ", ask(1, x, y)); else if (s[0] == 'A') change(1, x, y); else change(1, x, -y); } // for(int i = 1; i <= 100; i++) if(t[i].l == 5 && t[i].r == 5) // printf("!!!%d ", t[i].sum); } int main() { // freopen("data.in", "r", stdin); // freopen("data.out", "w", stdout); int t; scanf("%d", &t); for (int i = 1; i <= t; i++) { printf("Case %d: ", i); solve(); } return 0; }
②区间修改+区间查询型(使用懒标记)
由于区间的大小可以限制为1,所以完全可以取代前一种线段树,但是实现起来稍微多了点东西.
下列操作复杂度同上,实现参考(照搬)了<<指南>>,将会完成一个同时维护了区间和,区间最大值,支持区间操作的线段树.
1.建树
struct ST{ int l, r, big, sum; int tag; #define l(x) st[x].l #define r(x) st[x].r #define big(x) st[x].big #define sum(x) st[x].sum #define tag(x) st[x].tag }st[400010]; // 4 * N int n, q; void build(int p, int l, int r){ l(p) = l, r(p) = r; if(l == r) {sum(p) = 0; big(p) = 0; return;} int mid = l + r >> 1; build(p * 2, l, mid); build(p * 2 + 1, mid + 1, r); sum(p) = sum(p * 2) + sum(p * 2 + 1); big(p) = max(big(p * 2), big(p * 2 + 1)); }
2.区间修改+传递懒标记
void spread(int p){ if(!tag(p)) return; big(p * 2) += tag(p), big(p * 2 + 1) += tag(p); sum(p * 2) += tag(p) * (r(p * 2) - l(p * 2) + 1); sum(p * 2 + 1) += tag(p) * (r(p * 2 + 1) - l (p * 2 + 1) + 1); tag(p * 2) += tag(p), tag(p * 2 + 1) += tag(p); tag(p) = 0; } void change(int p, int l, int r, int x){ if(l <= l(p) && r >= r(p)) { big(p) += x; sum(p) += x * (r(p) - l(p) + 1); tag(p) += x; return; } spread(p); int mid = l(p) + r(p) >> 1; if(l <= mid) change(p * 2, l, r, x); if(r > mid) change(p * 2 + 1, l, r, x); sum(p) = sum(p * 2) + sum(p * 2 + 1); big(p) = max(big(p * 2), big(p * 2 + 1)); }
3.区间查询
int ask_big(int p, int l, int r){ if(l <= l(p) && r >= r(p)) return big(p); spread(p); int mid = l(p) + r(p) >> 1; int ret = 0; if(l <= mid) ret = max(ret, ask_big(p * 2, l, r)); if(r > mid) ret = max(ret, ask_big(p * 2 + 1, l, r)); return ret; } int ask_sum(int p, int l, int r){ if(l <= l(p) && r >= r(p)) return sum(p); spread(p); int mid = l(p) + r(p) >> 1; int ret = 0; if(l <= mid) ret += ask_sum(p * 2, l, r); if(r > mid) ret += ask_sum(p * 2 + 1, l, r); return ret; }
关于懒标记:在上面的实现里,每当调用spread(p)传递懒标记后,节点p及其子节点p*2,p*2+1的值均成为最新的(即正确的)状态,并且p的懒标记被利用后合理地清除了,而其子节点p*2,p*2+1的懒标记则仍然存在并且根据p的懒标记进行了更新.
这意味着懒标记最终会被传递到叶子节点上,注意叶子节点具不具有懒标记并不能说明叶子节点是否最新(从而正确),而叶子节点的懒标记是不会传递下去的(因为相关的函数在递归到叶子时一定会在spread之前return).
并且,在上面的change和ask函数里,发现有直接使用标记修改值的操作而不是调用spread.这是因为由于递归,当函数对这个节点调用时,可以保证这个节点自身的状态(在change中,是更改前;在aks中,是现在)是最新的,只需要将其标记向下传递即可.
最后放一道使用了稍微复杂一点的懒标记的题目.
这里维护了一个可以同时进行区间增加和区间数乘操作的线段树.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <string> #include <set> using namespace std; struct ST{ int l, r; long long sum, tagA, tagM = 1; #define l(x) st[x].l #define r(x) st[x].r #define sum(x) st[x].sum #define tagA(x) st[x].tagA #define tagM(x) st[x].tagM }st[400010]; // 4 * N int n, q, M; long long a[100010]; void spread(int p){ if(!tagA(p) && tagM(p) == 1) return; sum(p * 2) = (sum(p * 2) * tagM(p) % M + tagA(p) * (r(p * 2) - l(p * 2) + 1) % M) % M; sum(p * 2 + 1) = (sum(p * 2 + 1) * tagM(p) % M + tagA(p) * (r(p * 2 + 1) - l(p * 2 + 1) + 1) % M) % M; tagA(p * 2) = (tagA(p * 2) * tagM(p) % M + tagA(p)) % M, tagM(p * 2) = tagM(p * 2) * tagM(p) % M; tagA(p * 2 + 1) = (tagA(p * 2 + 1) * tagM(p) % M + tagA(p)) % M, tagM(p * 2 + 1) = tagM(p * 2 + 1) * tagM(p) % M; tagA(p) = 0, tagM(p) = 1; } void add(int p, int l, int r, int x){ if(l <= l(p) && r >= r(p)) { sum(p) = (sum(p) + x * (r(p) - l(p) + 1)) % M; tagA(p) = (tagA(p) + x) % M; return; } spread(p); int mid = l(p) + r(p) >> 1; if(l <= mid) add(p * 2, l, r, x); if(r > mid) add(p * 2 + 1, l, r, x); sum(p) = (sum(p * 2) + sum(p * 2 + 1)) % M; } void mul(int p, int l, int r, int x){ if(l <= l(p) && r >= r(p)){ sum(p) = (sum(p) * x) % M; tagM(p) = (tagM(p) * x) % M; tagA(p) = (tagA(p) * x) % M; return; } spread(p); int mid = l(p) + r(p) >> 1; if(l <= mid) mul(p * 2, l, r, x); if(r > mid) mul(p * 2 + 1, l, r, x); sum(p) = (sum(p * 2) + sum(p * 2 + 1)) % M; } void build(int p, int l, int r){ l(p) = l, r(p) = r; if(l == r) {sum(p) = a[l]; return;} int mid = l + r >> 1; build(p * 2, l, mid); build(p * 2 + 1, mid + 1, r); sum(p) = (sum(p * 2) + sum(p * 2 + 1)) % M; } int ask(int p, int l, int r){ if(l <= l(p) && r >= r(p)) return sum(p); spread(p); int mid = l(p) + r(p) >> 1; int ret = 0; if(l <= mid) ret += ask(p * 2, l, r); if(r > mid) ret += ask(p * 2 + 1, l, r); return ret % M; } int main(){ scanf("%d%d%d", &n, &q, &M); for(int i = 1; i <= n; i++) scanf("%lld", a + i); build(1, 1, n); while(q--){ int opr, x, y, k; scanf("%d%d%d", &opr, &x, &y); if(opr == 1){ scanf("%d", &k); mul(1, x, y, k); }else if(opr == 2){ scanf("%d", &k); add(1, x, y, k); }else printf("%d ", ask(1, x, y) % M); } return 0; }
