Singular Value Decomposition
矩阵分解,特征值
- 矩阵的特征值分解的原理
- 目的是什么
- 如何去使用。
1.SVD矩阵分解
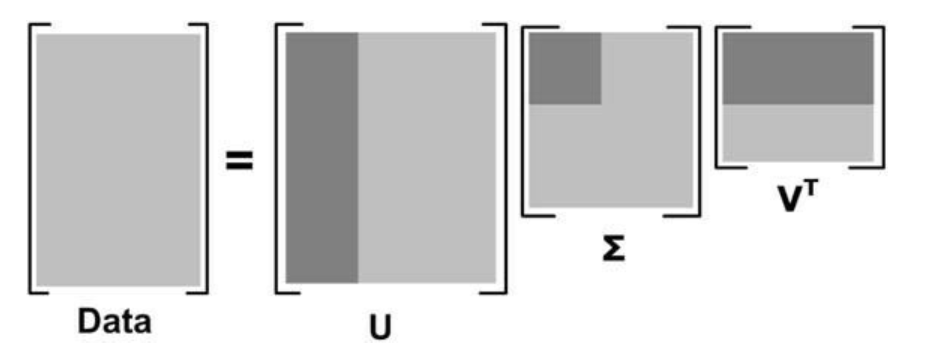
任意实矩阵(Ain R^{m * n})都可以进行分解$$A=U Sigma V^{T}$$
(Uin R^{m*m})是满足 (U^{T}U=I)的m阶酉矩阵 unitary matrix
(Vin R^{m*m}, V^{T} V=I)的n阶酉矩阵
(Sigma in R^{m*n})是m x n矩阵,其中(Sigma _{ii}=sigma _{i})
(sigma_{i})为非负数,满足(sigma_{1} geq sigma_{2}geq ...geq 0)
知识点扩充:酉矩阵
n阶复方阵U的n个列向量是U空间的一个标准正交基。酉矩阵是正交矩阵往复数域的推广
一些性质
1.(sigma_{i})奇异值按降序排列确保(Sigma)的唯一性
2.矩阵(A)的秩就是非零奇异值的个数
3.矩阵(A)的奇异值就是矩阵(A*A^{T})特征值的平方根
2.SVD的实现
利用numpy函数包中linalg来实现
# 先看一个具体的案例
import numpy as np
U,Sigma,VT=np.linalg.svd([[1,1],[7,7]])
print("the U is:
{}
Sigma is:
{}
VT is:
{}".format(U,Sigma,VT));
输出
the U is:
[[-0.14142136 -0.98994949]
[-0.98994949 0.14142136]]
Sigma is:
[1.00000000e+01 2.82797782e-16]
VT is:
[[-0.70710678 -0.70710678]
[ 0.70710678 -0.70710678]]
这里要注意的是在numpy中为了节省储存空间,特征值矩阵Sigma 只输出对角线的元素(输出一列)
from numpy import *
from numpy import linalg as la
# construct the datasets
def loadExData():
return[[0, 0, 0, 2, 2],
[0, 0, 0, 3, 3],
[0, 0, 0, 1, 1],
[1, 1, 1, 0, 0],
[2, 2, 2, 0, 0],
[5, 5, 5, 0, 0],
[1, 1, 1, 0, 0]]
if __name__ == '__main__':
data=loadExData()
U,Sigma,VT=linalg.svd(data)
print("Sigma is:
{}".format(Sigma))
输出结果:
Sigma is:
[9.64365076e+00 5.29150262e+00 6.49628424e-16 1.43063514e-16 2.79192092e-17]
开始对矩阵进行约简
采用启发式的策略来保留奇异值的数目:
- 保留矩阵中90%的能量信息-所有奇异值的平方和为总能量,奇异值平方和累加到90%就可以。
- 在科学和工程中,我们一般设置在r个奇异值之后,其余的奇异值都为0(非常小)。表示在数据集中只有r个重要特征,其余的特征都是噪声或者冗余特征。r=2000或3000
def Sigma(data):
U,Sigma,VT=linalg.svd(data)
return U,Sigma,VT
def SigmaReduce(U,Sigma,VT):
sigmaReduce=mat([[Sigma[0],0],[0,Sigma[1]]])
similarMatrix=U[:,:2]*sigmaReduce*VT[:2,:]
return similarMatrix
if __name__ == '__main__':
data=loadExData()
U,Sigma,VT=Sigma(data)
similarMatrix=SigmaReduce(U,Sigma,VT)
print("the similarMatrix is :
{}".format(similarMatrix))
结果是:
the similarMatrix is :
[[ 1.76986622e-17 -7.05283417e-16 -7.05283417e-16 2.00000000e+00 2.00000000e+00]
[ 7.22982080e-16 -3.61491040e-16 -3.61491040e-16 3.00000000e+00 3.00000000e+00]
[ 2.40994027e-16 -1.20497013e-16 -1.20497013e-16 1.00000000e+00 1.00000000e+00]
[ 1.00000000e+00 1.00000000e+00 1.00000000e+00 -1.70292592e-16 -1.70292592e-16]
[ 2.00000000e+00 2.00000000e+00 2.00000000e+00 -2.45454840e-16 -2.45454840e-16]
[ 5.00000000e+00 5.00000000e+00 5.00000000e+00 -5.55011948e-18 -5.55011948e-18]
[ 1.00000000e+00 1.00000000e+00 1.00000000e+00 -1.22727420e-16 -1.22727420e-16]]
与原始数据相比较,几乎没有什么差距
表示可以使用sigma来进行代替约简矩阵
3.SVD的实际应用
基于协同过滤的推荐引擎
协同过滤-collaborative filtering
相似度的计算
- 欧式距离计算相似度
p=2的时候表示为欧式距离
可以利用 $$simiarity=frac{1}{1+L_{p}distance}$$
来保证相似度在(0,1)之间,数值越大表示相似度越高。
- Pearson correlation
在 numpy计算包中,可以使用 corrcoef()函数来实现计算
corrcoef()的输出是(-1,1),可以使用函数 0.5+0.5*corrcoef() 来将输出相似度保证在(0,1)之间
- 余弦相似度-cosine similarity
(mid mid A mid mid ,mid mid B mid mid) 表示向量的2范数
夹角为90度,则相似度为0,方向相同则相似度为1。
范数的计算方法可以使用 numpy.linalg.norm()来计算
推荐引擎评价指标:最小均方根误差 root mean squared error RSME
对数字识别的图像进行压缩
结果是使用两个特征值就可以实现矩阵的近似,实现图像的重构
大大减小了存储空间
# import packages
def printMat(inMat,thresh=0.8):
for i in range(32):
for k in range(32):
if float(inMat[i,k])>thresh:
print("{}".format(1))
else:
print("{}".format(0))
print("
")
def imgCompress(numSV=3,thresh=0.8):
myl=[]
for line in open('0_5.txt').readlines():
newRow=[]
for i in range (32):
newRow.append(int(line[i]))
myl.append(newRow)
myMat=mat(myl)
# firsr,print the original matrix
print(" the original matrix")
printMat(myMat,thresh)
U,Sigma,VT=la.svd(myMat)
sigRecon=mat(zeros((numSV,numSV)))
# 还是需要把简化的 sigma 变成矩阵的形式
for k in range(numSV):
sigRecon[k,k]=Sigma[k]
# 计算推荐矩阵
ReconMat=U[:,:numSV]*sigRecon*VT[:numSV,:]
# print the recommend matrix
print("the recommend matrix ")
printMat(ReconMat,thresh)
if __name__ == '__main__':
imgCompress()