参考资料:
https://blog.csdn.net/roll_keyboard/article/details/81127266
https://www.luogu.com.cn/blog/fzber0103/Li-Chao-Tree
前置知识:
线段树
求直线或线段之间的交点
李超线段树
李超线段树是巨佬李超发明的一种可以求函数定点最值的线段树,又名李超树。代码简短,思想简明,用途广泛。 。历年省选常出李超树模板题,或者会把李超树和树链剖分一起考(强行让李超上树)。蒟蒻先放道例题:
。历年省选常出李超树模板题,或者会把李超树和树链剖分一起考(强行让李超上树)。蒟蒻先放道例题:
强制在线,(n) 个操作:
- 在平面上加入一条线段,两端端点为 ((x_0,y_0)) 和 ((x_1,y_1))。记第 (i) 条被插入的线段的标号为 (i)。
- 给定整数 (k),询问与 (x=k) 相交的线段中,交点纵坐标最大的线段的编号。
数据范围:(1le nle 10^5),(1le k,x_0,x_1le 39989),(1le y_0,y_1le 10^9)。
李超线段树的结构和普通线段树一样的,只是它每个节点存的是该区间优势最大的线段(优势最大即暴露在最高折线中横坐标跨度最大)。
如下图:
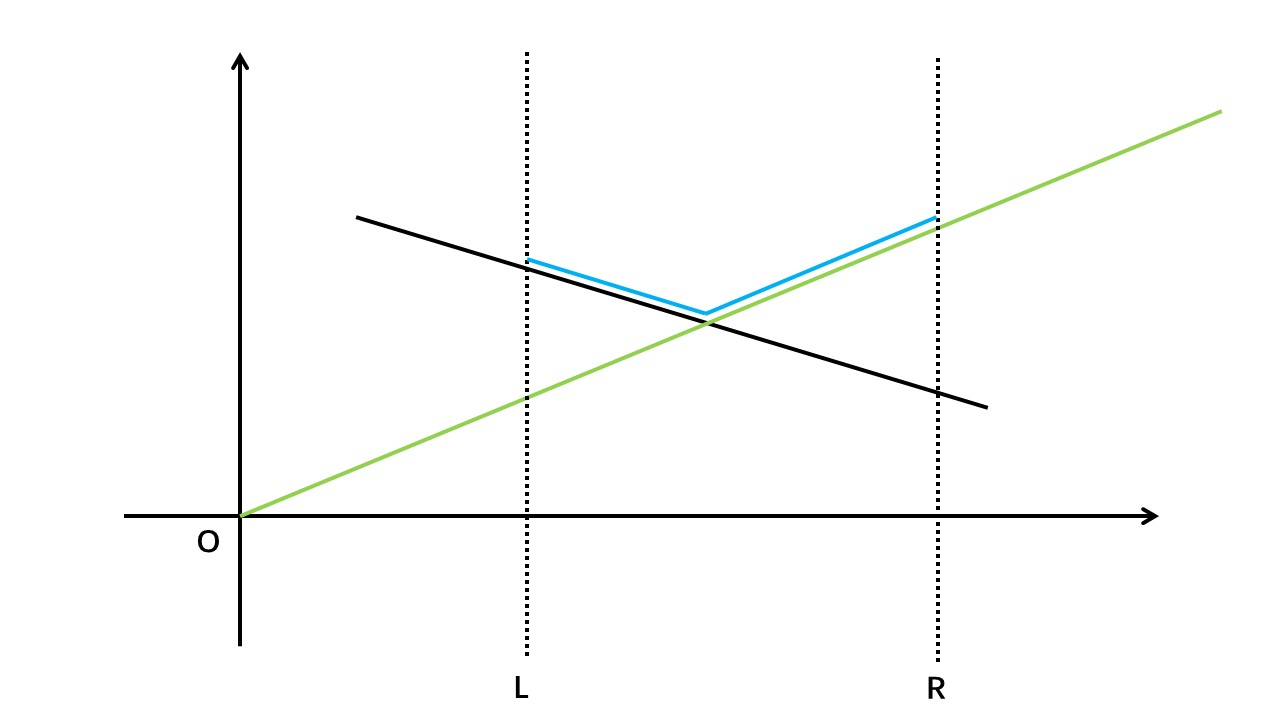
区间 ([L,R]) 中,蓝色折线为最高折线,绿色线段为该区间的优势最大线段。
重点:
李超线段树并不严格,只需满足包括单点的所有线段树区间“优势最大线段”中含有该单点的优势最大线段即可。这个性质使得李超树 (Theta(nlog n)) 的时间复杂度得以保障。所以会出现如果一整个区间最高折线都被一条线段占了的话,只有最大的区间的“优势最大线段”是该线段的情况。
那么新加进一条线段的时候,如何更新区间 ([L,R]) 以及其子区间的优势最大线段呢?可以分类讨论:
① 该区间还没有线段:直接修改,让加进去的线段当王。
② 该区间有优势最大线段,但是加进的线段两端区间两端点都低于当前最大优势线段,那么不管新线段:
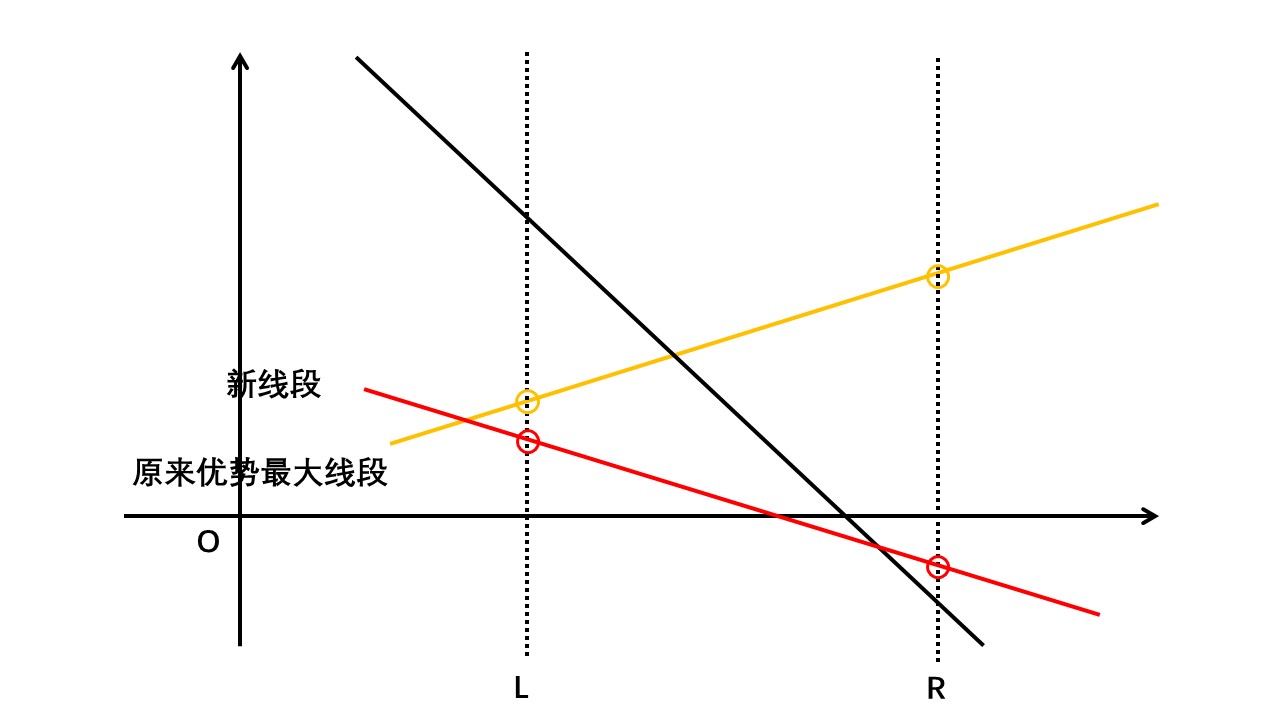
③ 该区间有优势最大线段,但是加进的线段两端区间两端点都高于当前最大优势线段,那么该区间的最大优势线段换成新加进的线段:
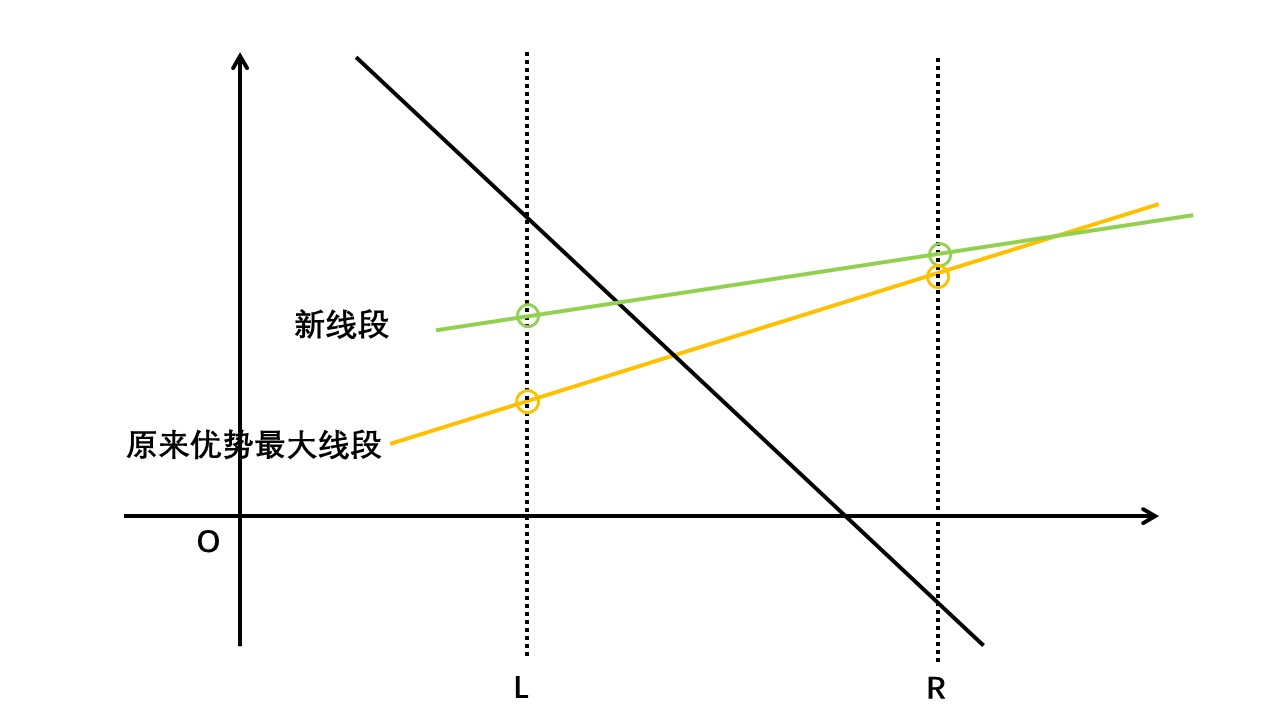
④ 该区间有优势最大线段,但是加进去的线段在区间内和原最大优势线段有交点,那么再分类讨论:
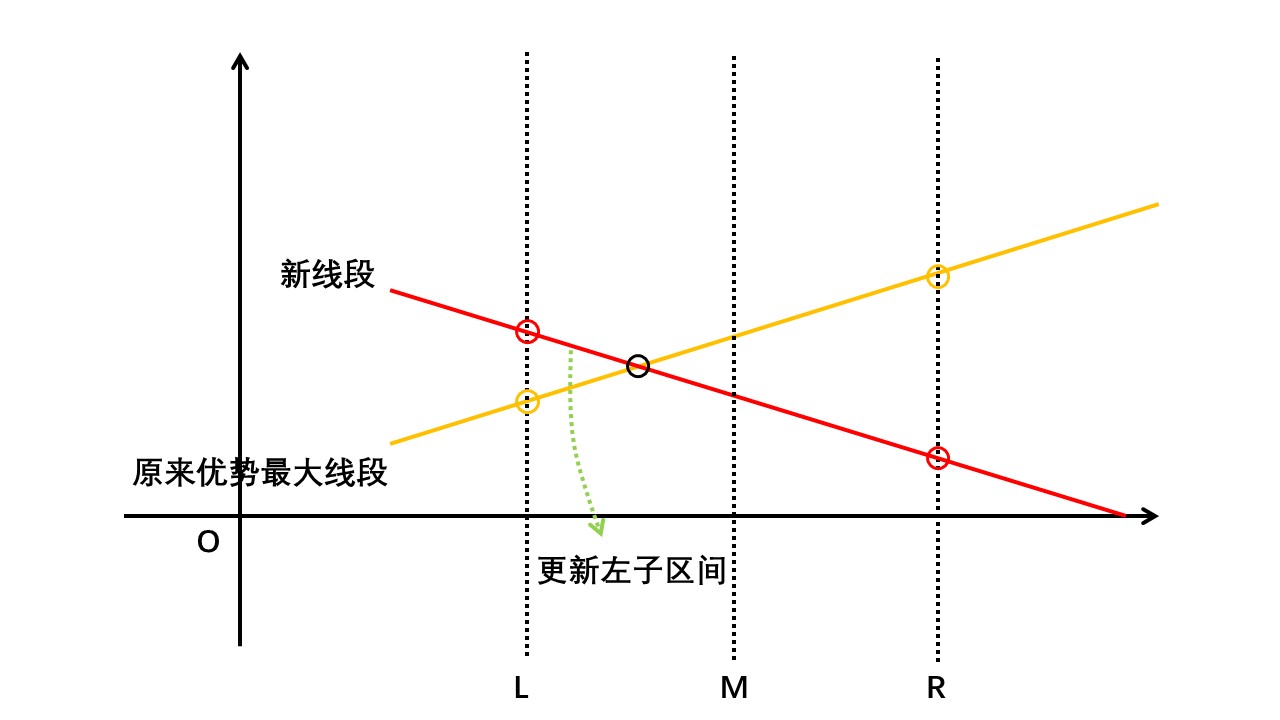
① 新线段与区间左端点交点高于原最大优势线段:
① 交点位于区间中点及其左侧,那么不更新该区间最大优势线段但是用新线段更新该区间左子区间最大优势线段:
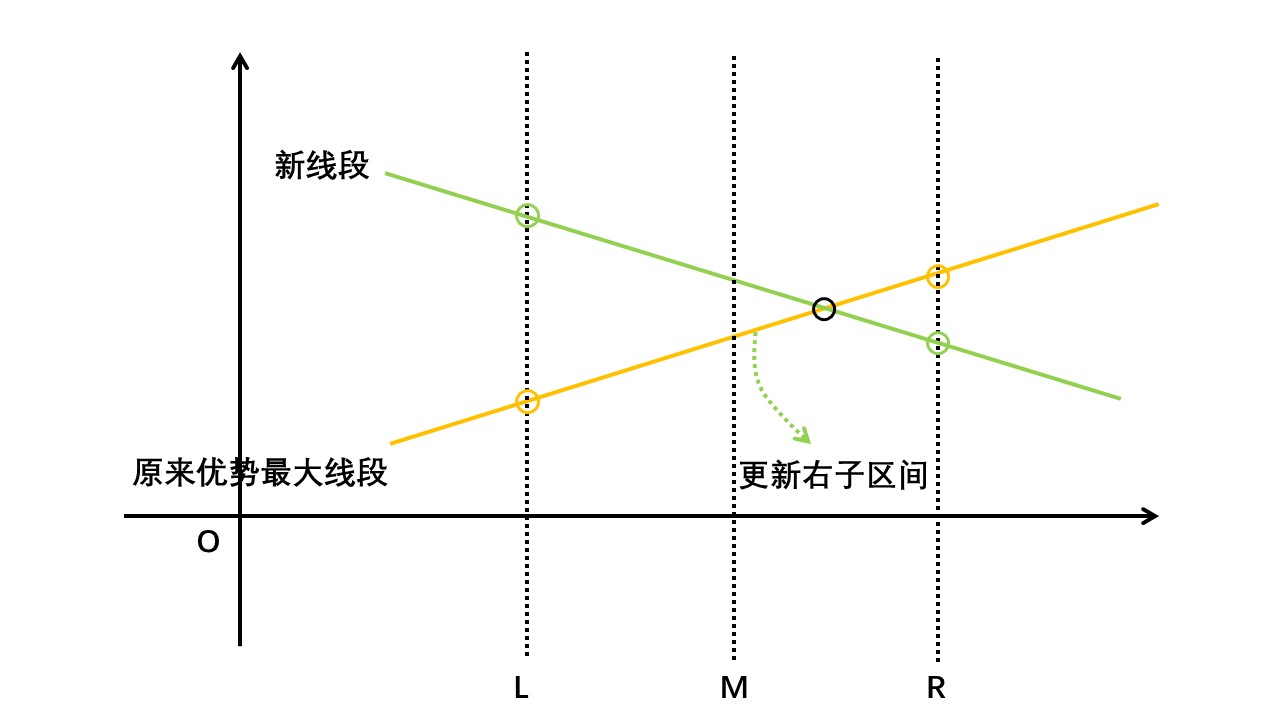
② 交点位于区间中点右侧,那么更新该区间最大优势线段为新线段但是用原最大优势线段更新该区间右子区间最大优势线段:
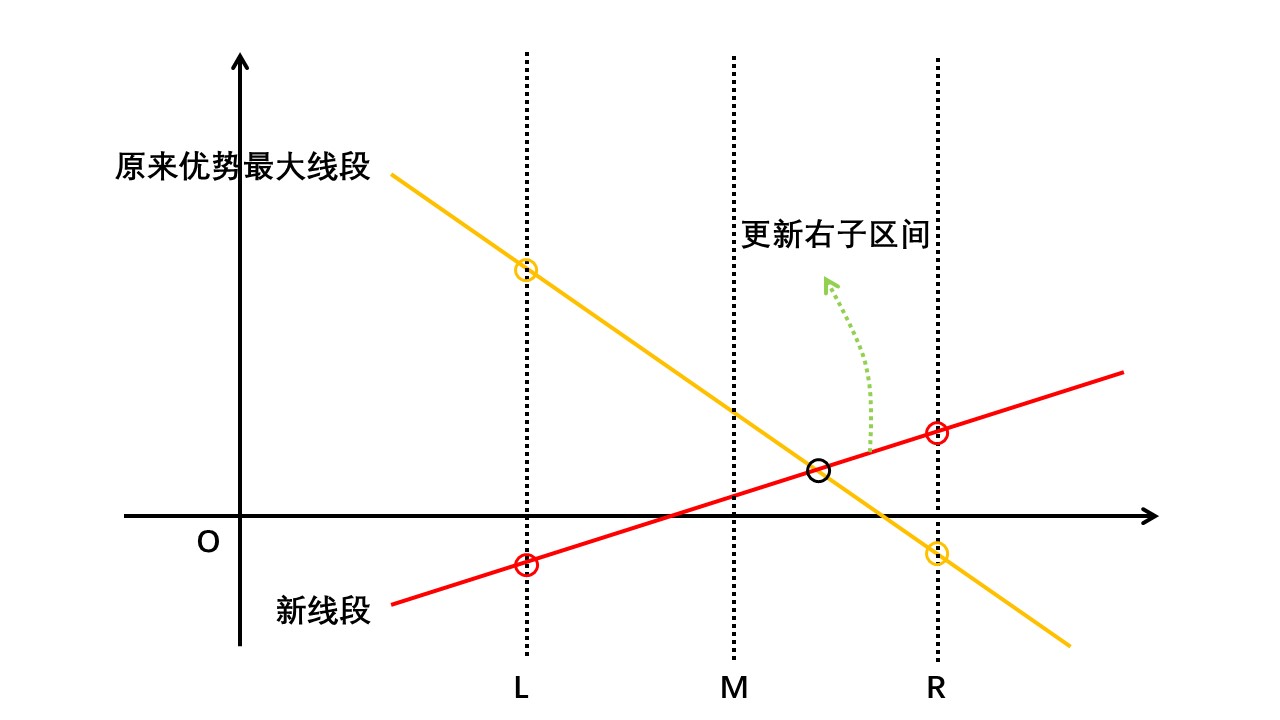
② 新线段与区间右端点交点高于原最大优势线段:
① 交点位于区间中点右侧,那么不更新该区间最大优势线段但是用新线段更新该区间右子区间最大优势线段:
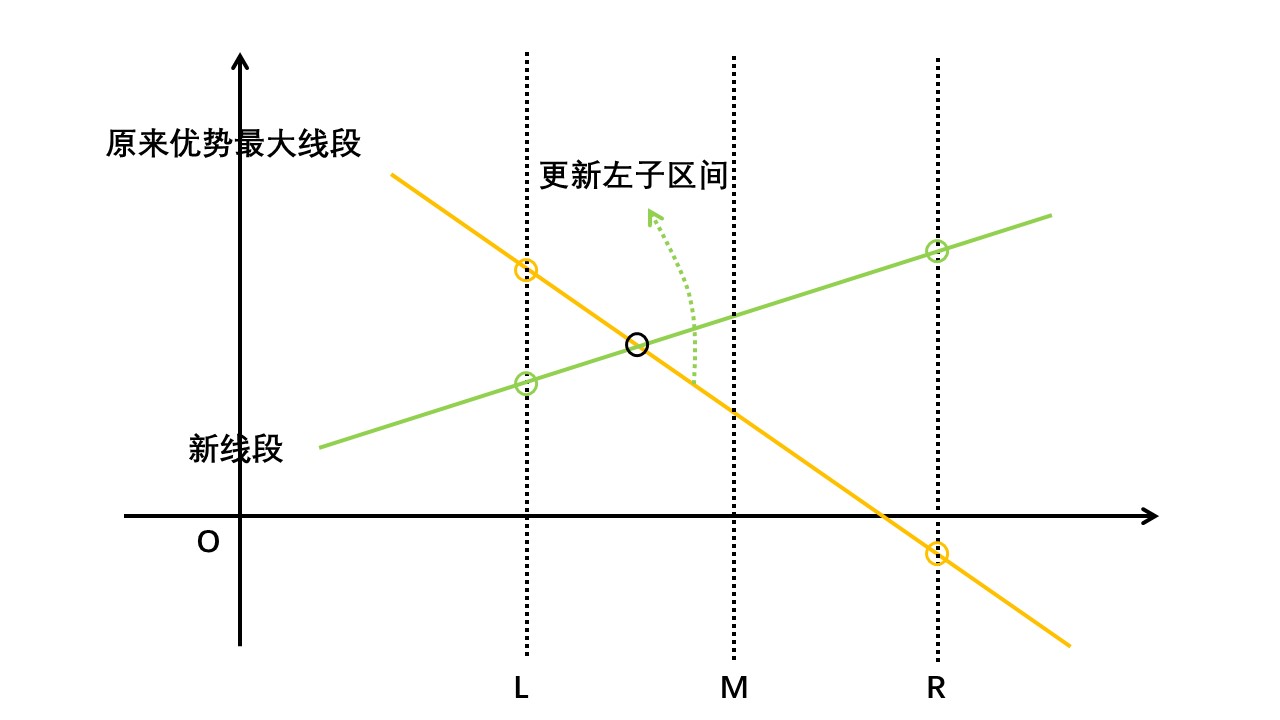
② 交点位于区间中点及其左侧,那么更新该区间最大优势线段为新线段但是用原最大优势线段更新该区间左子区间最大优势线段:
代码:
void add(int x,int L,int R,int k=1,int l=1,int r=M){
int mid=(l+r)>>1;
if(L<=l&&r<=R){
if(!ma[k]){v[k]=x,ma[k]=1;return;}
db ly1=f(li[x],l),ry1=f(li[x],r),ly=f(li[v[k]],l),ry=f(li[v[k]],r);
if(ly1<=ly&&ry1<=ry) return;
if(ly1>=ly&&ry1>=ry){v[k]=x;return;}
db in=inter(li[v[k]],li[x]);
if(ly1>=ly){
if(in<=mid) add(x,L,R,k<<1,l,mid);
else add(v[k],L,R,k<<1|1,mid+1,r),v[k]=x;
} else {
if(in>mid) add(x,L,R,k<<1|1,mid+1,r);
else add(v[k],L,R,k<<1,l,mid),v[k]=x;
}
return;
}
if(mid>=L) add(x,L,R,k<<1,l,mid);
if(mid<R) add(x,L,R,k<<1|1,mid+1,r);
}
那么如何求与 (x=k) 相交的线段中,交点纵坐标最大的线段的编号呢?
依次枚举包含 (k) 的线段树区间,取每个区间的最大优势线段的对应纵坐标的最大值即可。
代码:
int lccmp(int X,int x,int y){return f(li[x],X)>f(li[y],X)?x:y;}
int get(int X,int k=1,int l=1,int r=M){
int res=0;
if(ma[k]) res=lccmp(X,res,v[k]);
if(l==r) return res;
int mid=(l+r)>>1;
if(mid>=X) res=lccmp(X,res,get(X,k<<1,l,mid));
else res=lccmp(X,res,get(X,k<<1|1,mid+1,r));
return res;
}
另外,对于这道例题,题面中恶意提到了会有线段垂直于 (x) 轴的情况,怎么办呢(因为线段是通过一次方程存储的)?
很简单,因为这道题只关注单点最值,所以可以把线段 (((x_0,y_0),(x_0,y_1))[y_0<y_1]) 转化为 (((x_0,y_1),(x_0,y_1))),存储为 (y=0x+y_1[x_0le xle x_0])。
如果你懂了,小小蒟蒻就放代码了 :
:
#include <bits/stdc++.h>
using namespace std;
//Start
#define lng long long
#define db double
#define mk make_pair
#define pb push_back
#define fi first
#define se second
#define rz resize
const int inf=0x3f3f3f3f;
const lng INF=0x3f3f3f3f3f3f3f3f;
//Data
const int N=1e5,M=39989;
int n,lcnt;
typedef pair<db,db> line;
db f(line x,int X){return x.fi*X+x.se;}
db inter(line x,line y){return (y.se-x.se)/(x.fi-y.fi);}
line li[N+7];
//Licaotree
int v[(N<<2)+7]; bitset<(N<<2)+7> ma;
void add(int x,int L,int R,int k=1,int l=1,int r=M){
int mid=(l+r)>>1;
if(L<=l&&r<=R){
if(!ma[k]){v[k]=x,ma[k]=1;return;}
db ly1=f(li[x],l),ry1=f(li[x],r),ly=f(li[v[k]],l),ry=f(li[v[k]],r);
if(ly1<=ly&&ry1<=ry) return;
if(ly1>=ly&&ry1>=ry){v[k]=x;return;}
db in=inter(li[v[k]],li[x]);
if(ly1>=ly){
if(in<=mid) add(x,L,R,k<<1,l,mid);
else add(v[k],L,R,k<<1|1,mid+1,r),v[k]=x;
} else {
if(in>mid) add(x,L,R,k<<1|1,mid+1,r);
else add(v[k],L,R,k<<1,l,mid),v[k]=x;
}
return;
}
if(mid>=L) add(x,L,R,k<<1,l,mid);
if(mid<R) add(x,L,R,k<<1|1,mid+1,r);
}
int lccmp(int X,int x,int y){return f(li[x],X)>f(li[y],X)?x:y;}
int get(int X,int k=1,int l=1,int r=M){
int res=0;
if(ma[k]) res=lccmp(X,res,v[k]);
if(l==r) return res;
int mid=(l+r)>>1;
if(mid>=X) res=lccmp(X,res,get(X,k<<1,l,mid));
else res=lccmp(X,res,get(X,k<<1|1,mid+1,r));
return res;
}
//Main
int ans;
void h(int&x,int mod){x=(x+ans-1)%mod+1;}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int op; scanf("%d",&op);
if(op){
int xa,ya,xb,yb;
scanf("%d%d%d%d",&xa,&ya,&xb,&yb);
h(xa,M),h(ya,1e9),h(xb,M),h(yb,1e9);
li[++lcnt]=xa==xb?mk(.0,db(max(ya,yb))):mk(db(yb-ya)/(xb-xa),-db(yb-ya)/(xb-xa)*xa+ya);
add(lcnt,min(xa,xb),max(xa,xb));
} else {
int k; scanf("%d",&k),h(k,M);
printf("%d
",ans=get(k));
}
}
return 0;
}
放几道例题练习练习:
祝大家学习愉快!