noip模拟测试9

---

T1：给出n个正整数a1,a2…an和一个质数mod.一个变量x初始为1.

　　进行m次操作.每次在n个数中随机选一个ai,然后$\mathrm{x=x\ast ai.问m次操作之后x的取值的期望.}$

$\mathrm{（1<=ai<mod\; \; mod为质数 \; \; 1<=mod<=1000\; \; 1<=n<=105\; ,\; 1<=m<=109）}$

$\mathrm{第一眼康上去感觉是个数论加期望，完全不想做，想想后发现是个假期望，但好像是真数论，还是不想做}$

$\mathrm{于是直接跳过，最后也没什么思路，打了个n\times m\times mod的暴力，然后喜暴\; 0}$

$\mathrm{考完后，听大佬们分享，才想到这是个矩阵优化dp}$

$\mathrm{那说说思路：}$

$\mathrm{首先会发现mod极小，而m极大，那么最基本的思路就是用mod复杂度增加的代价将m的复杂度降低}$

$\mathrm{猜测m复杂度为log级别，那么就想log级的算法}$

$\mathrm{想到如果设计一个状态\; f\; [\; i\; ][\; j\; ]\; 表示操作\; i\; 此后变成\; j\; 的期望}$

$\mathrm{那么每次转移的系数矩阵都是相同的！}$

$\mathrm{我们就可以用矩阵快速幂来优化dp的转移，于是复杂度为：O\; (\; mod3\; log(m)\; )}$

$\mathrm{可是还是过不了，思路有问题吗？显然没有，那怎么优化呢？}$

$\mathrm{关于矩乘的优化，想到循环矩阵的优化，于是看能不能转变系数矩阵的定义，让其成为循环矩阵}$

$\mathrm{发现题目一个很妙的性质，1<=ai<mod，于是想到用原根优化（？？？）}$

$\mathrm{设原根为\; rt\; ，若\; i\; =\; xp[i]\; 那么，我们最开始的式子是\; i\; \times \; ak\; \to \; j\; (mod\; mod)}$

$\mathrm{那么用原根就可以将式子转化为\; xp[i]\; \times \; xp[ak]\; =\; xp[j]\; (mod\; mod)}$

$\mathrm{因为底数都是\; x\; ，所以我们可以将其转化为指数间的运算}$

$\mathrm{即：p[\; i\; ]\; +\; p[\; ak\; ]\; =\; p[\; j\; ]\; (mod\; \phi (mod))}$

$\mathrm{哇，加法！}$

$\mathrm{好了，它循环了。}$

$\mathrm{为什么？\; 加法的转移相当与一种等距离的定向的转移，所以必循环}$

$\mathrm{时间复杂度变为\; O\; (\; mod2\; log(m)\; )\; ,同时还优化了空间的复杂度}$

$\mathrm{so，code}$

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#define ll long long
using namespace std;
const int MAXMOD=1005,MAXN=100005,D=1e9+7;
int n,m,mod;
ll val[MAXN],ans,prt,pos[MAXMOD],cnt[MAXMOD],stk[MAXMOD],tp,invn;
struct Matrix {
    ll s[MAXMOD];
    Matrix() {memset(s,0,sizeof(s));}
}P,R;
Matrix operator * (const Matrix &AA,const Matrix &BB) {
    Matrix CC;
    for(int i=0;i<mod;i++)
        for(int j=0;j<mod;j++)
            CC.s[(i+j)%(mod-1)]=(CC.s[(i+j)%(mod-1)]+AA.s[i]*BB.s[j]%D)%D;
    return CC;
}    
ll qpow(ll x,ll k,ll dd) {
    ll ret=1;
    while(k) {
        if(k&1) ret=(ret*x)%dd;
        x=(x*x)%dd,k>>=1;
    }
    return ret%dd;
}
void get_prt() {
    int tmp=mod-1;
    for(int i=2;i*i<mod;i++)
        if(tmp%i==0) {
            stk[++tp]=i;
            while(tmp%i==0) tmp/=i;
        }
    if(tmp>1) stk[++tp]=tmp;
    for(int i=2;i<=mod;i++) {
        bool flag=0;
        for(int j=1;j<=tp;j++)
            if(qpow(i,(mod-1)/stk[j],mod)==1) {flag=1;break;}
        if(!flag) {prt=i;break;}
    }
    for(int i=0;i<mod-1;i++) pos[qpow(prt,i,mod)]=i;
}
int main() {
    scanf("%d%d%d",&n,&m,&mod);
    for(int i=1;i<=n;i++) scanf("%lld",&val[i]),++cnt[val[i]];
    get_prt();
    invn=qpow(n,D-2,D);
    for(int i=1;i<mod;i++)
        P.s[pos[i]]=cnt[i]*invn%D;
    R.s[0]=1;
    while(m) {
        if(m&1) R=R*P;
        P=P*P,m>>=1;
    }
    for(int i=1;i<mod;i++) ans=(ans+R.s[pos[i]]*i)%D;
    printf("%lld
",ans);
    return 0;
}

---

---

T2：给一颗树，每个节点都有两个权值a和b，a和b有如下关系：

　　b[x]=a[1]dis(1,x)+a[2]dis(2,x)+....+a[n]*dis(n,x) （dis ( i , j ) 表示i 到j 的最短路径经过的边数）

　　现在给你a与b数组中的一个，求另一个数组。

　　( 2<=n<=100000 )

　　首先很容易就可以在 O ( n ) 的复杂度下利用换根dp用a求出b，dp方程显然，就不赘述了

　　

　　主要看如何用b来求a：

　　不妨设dp的根为1

$\mathrm{我们看a求b时换根的方程\; b[\; v\; ]\; =\; b[\; u\; ]\; +\; （siz[\; 1\; ]\; -\; siz\; [\; v\; ]）-\; siz\; [\; v\; ]}$

$\mathrm{（siz\; [\; i\; ]\; 表示以i为根的子树内a的和）（v是u的儿子）}$

$\mathrm{移项后得\; b[\; v\; ]\; -\; b[\; u\; ]\; =\; siz[\; 1\; ]\; -\; 2\times siz[\; v\; ]\; 记作\; g[\; v\; ]}$

$\mathrm{于是我们可以对除1以外的所以点进行上述计算}$

$\mathrm{然后会发现其实并算不出什么东西？？？}$

$\mathrm{可是我们还没有用\; b[\; 1\; ]\; 啊？}$

$\mathrm{于是将\; b[\; 1\; ]的表达式写出，然后再合并}$

$\mathrm{发现，b[\; 1\; ]\; =\; \sum siz\; [\; u\; ]\; (u!=1)}$

$\mathrm{那就简单了，用\; \sum g[\; v\; ]\; +\; 2\; \times \; b[\; 1\; ]\; 就可以计算出\; siz[\; 1\; ]\; 的值}$

$\mathrm{然后再用\; g\; 和\; siz[\; 1\; ]\; 算出所有点的\; siz}$

$\mathrm{最后dfs一遍求出a即可}$

$\mathrm{so，code}$

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#define ll long long
using namespace std;
const int MAXN=200005;
int T,n,o;
ll val[MAXN],siz[MAXN],f[MAXN],g[MAXN],sum;
struct node {
    int to,nxt;
}mp[MAXN*2];
int h[MAXN],tot;
void add(int x,int y) {
    mp[++tot].nxt=h[x];
    mp[tot].to=y;
    h[x]=tot;
}
void dfs1(int u,int fa) {
    siz[u]=val[u];
    for(int i=h[u];i;i=mp[i].nxt) {
        int v=mp[i].to;
        if(v==fa) continue;
        dfs1(v,u);
        siz[u]+=siz[v];
        f[u]+=f[v]+siz[v];
    }
}
void dfs2(int u,int fa) {
    for(int i=h[u];i;i=mp[i].nxt) {
        int v=mp[i].to;
        if(v==fa) continue;
        g[v]=g[u]-siz[v]+(siz[1]-siz[v]);
        dfs2(v,u);
    }
}
void work0() {
    dfs1(1,0);
    g[1]=f[1];
    dfs2(1,0);
    for(int i=1;i<=n;i++) printf("%lld ",g[i]);
    printf("
");
}
void dfs3(int u,int fa) {
    for(int i=h[u];i;i=mp[i].nxt) {
        int v=mp[i].to;
        if(v==fa) continue;
        g[v]=val[v]-val[u];
        dfs3(v,u);
    }
}
void dfs4(int u,int fa) {
    f[u]=siz[u];
    for(int i=h[u];i;i=mp[i].nxt) {
        int v=mp[i].to;
        if(v==fa) continue;
        dfs4(v,u);
        f[u]-=siz[v];
    }
}
void work1() {
    dfs3(1,0);
    for(int i=2;i<=n;i++) sum+=g[i];
    siz[1]=(2*val[1]+sum)/(n-1);
    for(int i=2;i<=n;i++) siz[i]=(siz[1]-g[i])/2;
    dfs4(1,0);
    for(int i=1;i<=n;i++) printf("%lld ",f[i]);
    printf("
");
}
int main() {
    scanf("%d",&T);
    while(T--) {
        scanf("%d",&n);
        for(int i=1,aa,bb;i<n;i++) scanf("%d%d",&aa,&bb),add(aa,bb),add(bb,aa);
        scanf("%d",&o);
        for(int i=1;i<=n;i++) scanf("%lld",&val[i]);
        if(!o) work0();
        else work1();
        memset(h,0,sizeof(h));
        memset(f,0,sizeof(f));
        memset(g,0,sizeof(g));
        memset(siz,0,sizeof(siz));
        memset(val,0,sizeof(val));
        tot=0;sum=0;
    }
    return 0;
}

---

---

T3：只能上下左右走，从(0,0)开始有限制的走n步之后回到(0,0)的方案数.

　　一共有三种限制,加上没有限制的情况,一共有四种情况,用0,1,2,3标号:
　　0.没有任何限制,可以到达坐标系上所有的点,即能到达的点集为{(x,y)|x,y为整数}
　　1.只允许到达x轴非负半轴上的点.即能到达的点集为{(x,y)|x为非负数,y=0}
　　2.只允许到达坐标轴上的点.即能到达的点集为{(x,y)|x=0或y=0}
　　3.只允许到达x轴非负半轴上的点,y轴非负半轴上的点以及第1象限的点.即能到达的点集为{(x,y)|x>=0,y>=0}

　　( 对于 0，1，3 情况 n <= 100000 ，对于 2 情况 n <= 1000 )

　　情况 0 ：

　　　　法一：可以很容易发现此题与noip模拟测试7中的T2就是一道题

　　　　　　　枚举一个方向的步数，计算出其他方向的步数，多重集排列一下就好了。

　　　　法二：将坐标轴旋转45^o （？？？）

　　　　　　　

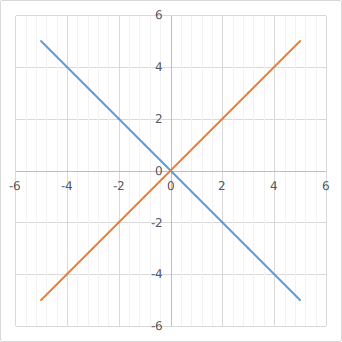
　　　　　　　橙色线和蓝色线分别对应原坐标的坐标轴

　　　　　　　容易看出，在原坐标系中上下左右任意走一步可以对应在新坐标轴上连续走x，y方向各一步

　　　　　　　即：x，y两方向的行动顺序固定！

　　　　　　　那么两个行动方案不同当且仅当不同方向的步数不同！　　　　　　　

　　　　　　　那就简单了，总共走n步，所以转化过来就是x上走n步，y上走n步

　　　　　　　x上有n/2步是向上，n/2是向下，因为顺序一定所以方案数为C ( n , n/2 )，y 同理

　　　　　　　所以答案就是 [ C ( n , n/2 ) ]² 

　　情况 1：显然，catalan数

　　情况 2：加个dp，f [ i ] 表示走 2×i 步 的方案数

　　　　　　注意到 n 在此情况情况较小，想 n² dp

　　　　　　首先可以看出行动的路径应该是从（0,0）走出，走回来，再转向;再走出……

　　　　　　于是我们只需要枚举最后一次走回来的时刻就行了

　　　　　　方程 ：f [ i ] = ∑ f [ j ] × catlan [ i - j -1] × 4

　　　　　　　　　　　　（…）   （出去再回来）（转向）

　　　　　　为什么是catalan第 i - j - 1 项而不是 i - j 项？

　　　　　　因为我们要使 j 是最后一个回到原点的时刻，所以我们不能再次走回原点

　　　　　　而对于任意一种2×a步不回原点的方案，都唯一对应一种：

　　　　　　先走出一步，再走 2×( a - 1 )步（可以回到出发点），最后走一步回来。

　　　　　　所以方案数就为 catlan [ a - 1 ]

　　情况 3 ：这一看不就是两个catalan怎么计算一下就出来的吗？

　　　　　　于是发现可以做个类似卷积的东西：

　　　　　∑catalan [ i ] * catalan [ n/2 - i ] * ( 2 * n/2 ) ! / (2 * i) / ( 2 * ( n/2 - i ) )
　　　　　
　　　　　即：在 x 方向走 2×i 步，在 y 方向走 2×（n/2 - i） 步
　　　　　
　　　　　
　　　　　so，code

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#define ll long long
using namespace std;
const int MAXN=100105,D=1e9+7;
ll n,op,ans,a,b,fac[MAXN],inv[MAXN],ct[MAXN],f[MAXN],g[MAXN];
ll qpow(ll x,ll k) {
    ll ret=1;
    while(k) {
        if(k&1) ret=(ret*x)%D;
        x=(x*x)%D;
        k>>=1;
    }
    return ret%D;
}
void first(ll lim) {
    fac[0]=inv[0]=fac[1]=1;
    for(int i=2;i<=lim;i++) fac[i]=(fac[i-1]*i)%D;
    inv[lim]=qpow(fac[lim],D-2);
    for(int i=lim-1;i>=1;i--) inv[i]=(inv[i+1]*(i+1))%D;
}
void work0() {
    first(n);
    for(int i=0;i<=n;i+=2) {
        a=(ll)i/2;
        b=(ll)(n-i)/2;
        ans=(ans+fac[n]*inv[a]%D*inv[a]%D*inv[b]%D*inv[b])%D;
    }
    printf("%lld
",(ans%D+D)%D);
}
void work1() {
    first(n),n/=2;
    ans=fac[2*n]*inv[n]%D*inv[n+1]%D;
    printf("%lld
",ans);
}
void work2() {
    first(n),n/=2;
    ct[0]=1;
    for(int i=1;i<=n;i++) ct[i]=fac[2*i]*inv[i+1]%D*inv[i]%D;
    f[0]=1;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=i;j++) f[i]=(f[i]+f[j]*ct[i-j-1]%D*4)%D;
    printf("%lld
",f[n]);
}
void work3() {
    first(n),n/=2;
    ct[0]=1;
    for(int i=1;i<=n;i++) ct[i]=fac[2*i]*inv[i+1]%D*inv[i]%D;
    for(int i=0;i<=n;i++)
        ans=(ans+ct[i]*ct[n-i]%D*fac[2*n]%D*inv[2*i]%D*inv[2*(n-i)]%D)%D;
    printf("%lld
",ans);
}
int main() {
    scanf("%lld%lld",&n,&op);
    if(op==0) work0();
    if(op==1) work1();
    if(op==2) work2();
    if(op==3) work3();
    return 0;
}

---