矩阵加、减法
矩阵加法非常简单,对应位置直接加减即可,但是前提是两个矩阵大小相同(即一个矩阵是N*M的,另一个与之相加的矩阵的大小也要是N*M)。就像这样:

矩阵乘法
矩阵乘法就相对比较复杂了。他需要满足的前提是第一个矩阵的列数要等于第二个矩阵的行数,这样的两个矩阵才可以相乘。下面我用一个图来解释怎么样进行矩阵乘法:
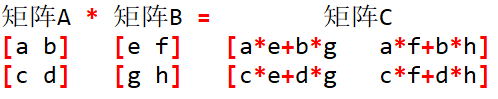
矩阵乘法性质:
①矩阵乘法满足乘法结合律————A*B*C=(A*B)*C=A*(B*C)
②矩阵乘法满足左分配律和右分配律————C*(A+B)=C*A+C*B || (A+B)*C=A*C+B*C
③矩阵乘法不满足交换律————A*B!=B*A
下面是矩阵乘法的代码:
#include<bits/stdc++.h>
using namespace std;
int m1[10][10],m2[10][10],m3[10][10]; //m1*m2=m3
int main(){
register int a,b,c;
//矩阵m1大小为n*m 矩阵m2大小为m*k 矩阵m3大小为n*k
for(a=1;a<=n;++a)
for(b=1;b<=m;++b)
for(c=1;c<=k;++c)
m3[a][c]+=m1[a][b]*m2[b][c];
return 0;
}
应用:矩阵乘法可以用来求斐波那契数列的第n项
用矩阵乘法求斐波那契数列的第n项,如果n比较的大的话就需要用到矩阵KSM了,不会的可以看一下这篇博客:https://www.cnblogs.com/Glacier-elk/p/9489655.html
洛谷原题链接:https://www.luogu.org/problemnew/show/P1962
在这道题目中保证n在long long的范围内,这就需要用到矩阵乘法和矩阵快速幂了。首先我们要知道怎么样用矩阵求斐波那契数列,也就是确定矩阵A和矩阵B分别是什么。其中一个矩阵肯定是存放斐波那契数列的,我们不妨就让矩阵A是斐波那契数列,让矩阵A是一个1*2的矩阵,分别存放第n项和第n-1项,则矩阵A可以表示为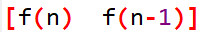
。那矩阵B就需要使A*B可以得到斐波那契的下一项。首先我们可以确定的是,矩阵B是一个2*2的矩阵,因为矩阵乘法需要满足一个矩阵的列数等于另一个矩阵的行数。所以我们不妨设矩阵B为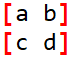 ,那么这样的话C就可以表示为
,那么这样的话C就可以表示为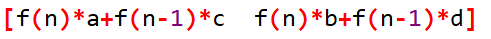 ,因为C也可以表示为
,因为C也可以表示为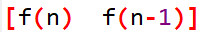 ,我们就可以用斐波那契数列的前几项列出几个方程组,就可以求出矩阵B的元素了。通过计算,我们发现矩阵B为
,我们就可以用斐波那契数列的前几项列出几个方程组,就可以求出矩阵B的元素了。通过计算,我们发现矩阵B为 。我们还可以发现,矩阵A每乘一次矩阵B,数列就可以向前递进一项,所以我们求第n项,就需要用矩阵A乘n-2遍矩阵B,也就是矩阵A乘矩阵B的n-2次方,这样我们就可以用矩阵快速幂求解。
。我们还可以发现,矩阵A每乘一次矩阵B,数列就可以向前递进一项,所以我们求第n项,就需要用矩阵A乘n-2遍矩阵B,也就是矩阵A乘矩阵B的n-2次方,这样我们就可以用矩阵快速幂求解。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
ll n,b[3][3],a[2][2],ans[3][3]={0,0,0,0,1,1,0,1,1},c[3][3];
void mul(int x){
register int i,j,k;
memset(c,0,sizeof(c));
for(i=1;i<=2;++i)
for(j=1;j<=2;++j)
for(k=1;k<=2;++k)
if(x) c[i][k]+=ans[i][j]*b[j][k],c[i][k]%=mod;
else c[i][k]+=b[i][j]*b[j][k],c[i][k]%=mod;
for(i=1;i<=2;++i)
for(j=1;j<=2;++j)
if(x) ans[i][j]=c[i][j];
else b[i][j]=c[i][j];
}
void ksm(ll cur){
while(cur){
if(cur & 1) mul(1);
cur>>=1;
mul(0);
}
printf("%lld",ans[1][1]%mod);
}
int main(){
ios::sync_with_stdio(false);
cin>>n;
if(n<=2){
cout<<"1";
return 0;
}
ans[1][1]=1,ans[1][2]=1,b[1][1]=1,b[1][2]=1,b[2][1]=1,b[2][2]=0;
ksm(n-2);
return 0;
}