参考:http://www.matrix67.com/blog/archives/120
前置:
广义组合数:C(n,m)=n·(n-1)·……·(n-m+1)/m! (n∈R,m∈N)
广义二项式定理: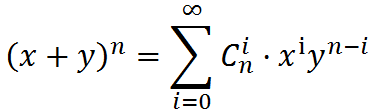
等比数列求和公式:a1+a1·q+a1·q2+a1·q3+……a1·qn=a1(1-qn+1)/(1-q)
无穷等比数列求和:a1+a1·q+a1·q2+a1·q3+……=a1/(1-q) (q∈(-1,1))
定义:
对于数列a0,a1,a2,a3……,定义其生成函数为f(x)=a0+a1·x+a2·x2+a3·x3+……
如对于数列ai=C(n,i),生成函数为f(x)=(1+x)n。
很多时候是无穷级数。
其中x没有实际意义,可以取任意值。
组合数学中用于各种计数问题。用次数表示所选物品个数,系数表示该选择的方案数,多项式相乘可以得到所选物品总数在各种情况下的方案数。
栗子:
我们要从苹果、香蕉、橘子和梨中拿一些水果出来,要求苹果只能拿偶数个,香蕉的个数要是5的倍数,橘子最多拿4个,梨要么不拿,要么只能拿一个。问按这样的要求拿n个水果的方案数。
构造出生成函数。
苹果:f(x)=1+x2+x4+x6+……=1/(1-x2)
香蕉:f(x)=1+x5+x10+x15+……=1/(1-x5)
橘子:f(x)=1+x+x2+x3+x4=(1-x5)/(1-x)
梨:f(x)=1+x
第一项1可以看做1·x0,后面每一项都省略了系数1。
其中苹果和香蕉都是无穷级数(虽然会受到n的限制)。因为x可以任意取值,不妨令x∈(-1,1),那么其收敛,就有了上面的结果。
将各式相乘,表示在每一类里各选择一种。一堆抵消之后,最终结果是1/(1-x)2。
这个结果看起来没什么意义,于是继续化式子。
1/(1-x)2=(1-x)-2=C(-2,0)·(-x)0+C(-2,1)·(-x)1+C(-2,2)·(-x)2+C(-2,3)·(-x)3+……
=1+2x+3x2+4x3……
稍微验证一下就会发现n次项对应的系数是选n个物品的方案数。
应用:
与多项式的各种运算搭配食用风味更佳。
经常可以用来捣鼓卷积形式的递推式。
好像也没什么好说的了。
(怎么感觉生成函数全是权限题啊好不友善啊)