最短路径算法——Floyd算法

基本思想： 
弗洛伊德算法定义了两个二维矩阵：

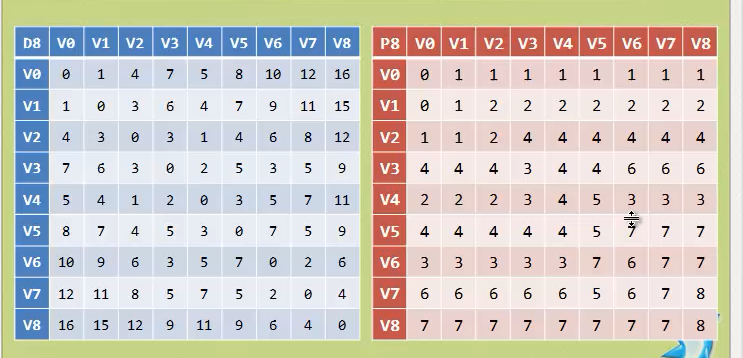
1. 矩阵D记录顶点间的最小路径 
   例如D[0][3]= 10，说明顶点0 到 3 的最短路径为10；
2. 矩阵P记录顶点间最小路径中的中转点 
   例如P[0][3]= 1 说明，0 到 3的最短路径轨迹为：0 -> 1 -> 3。

它通过3重循环，k为中转点，v为起点，w为终点，循环比较D[v][w] 和 D[v][k] + D[k][w] 最小值，如果D[v][k] + D[k][w] 为更小值，则把D[v][k] + D[k][w] 覆盖保存在D[v][w]中。

如下图：

对应的邻接矩阵

最终结果

代码：

#include <iostream>
#include <cstring>

#define MAX 9
#define INF 0xFFFF

int floyd(int matrix[][MAX], int prevPoint[][MAX], int finalP2V[][MAX])
{
    int i,j,k;

    for (i=0; i<MAX; i++)
        for (j=0; j<MAX; j++)
        {
            finalP2V[i][j] = matrix[i][j];
            prevPoint[i][j] = j;
        }

    for (k=0; k<MAX; k++)
        for (i=0; i<MAX; i++)
            for(j=0; j<MAX; j++)
            {
                if (finalP2V[i][j] > (finalP2V[i][k]+finalP2V[k][j]))
                {
                    finalP2V[i][j] = finalP2V[i][k]+finalP2V[k][j];
                    prevPoint[i][j] = prevPoint[i][k];
                }
            }
}

int main(int argc, char *argv[])
{
    int matrix[][MAX] = {{0, 1, 5, INF, INF, INF, INF, INF, INF},
                                  {1, 0, 3, 7, 5, INF, INF, INF, INF},
                                  {5, 3, 0, INF, 1, 7, INF, INF, INF },
                                  {INF, 7,INF, 0, 2, INF, 3, INF, INF},
                                  {INF, 5, 1, 2, 0, 3, 6, 9, INF},
                                  {INF, INF, 7, INF, 3, 0, INF, 5, INF},
                                  {INF, INF, INF, 3, 6, INF, 0, 2, 7},
                                  {INF, INF, INF, INF, 9, 5, 2, 0, 4},
                                  {INF, INF, INF, INF, INF, INF, 7, 4, 0}};

    int prevPoint[MAX][MAX] = {0};
    int finalP2V[MAX][MAX] = {0};

    floyd(matrix, prevPoint, finalP2V);

    for (int i=0; i<MAX; i++)
    {
        for (int j=0; j<MAX; j++)
        {
            std::cout << finalP2V[i][j] << " ";
        }
        std::cout << std::endl;
    }
}