注意到蓝线的产生方法,可以发现蓝线必然可以划分成若干个三个点中间由蓝线连成的情况,在树上就只有下面两种形式:
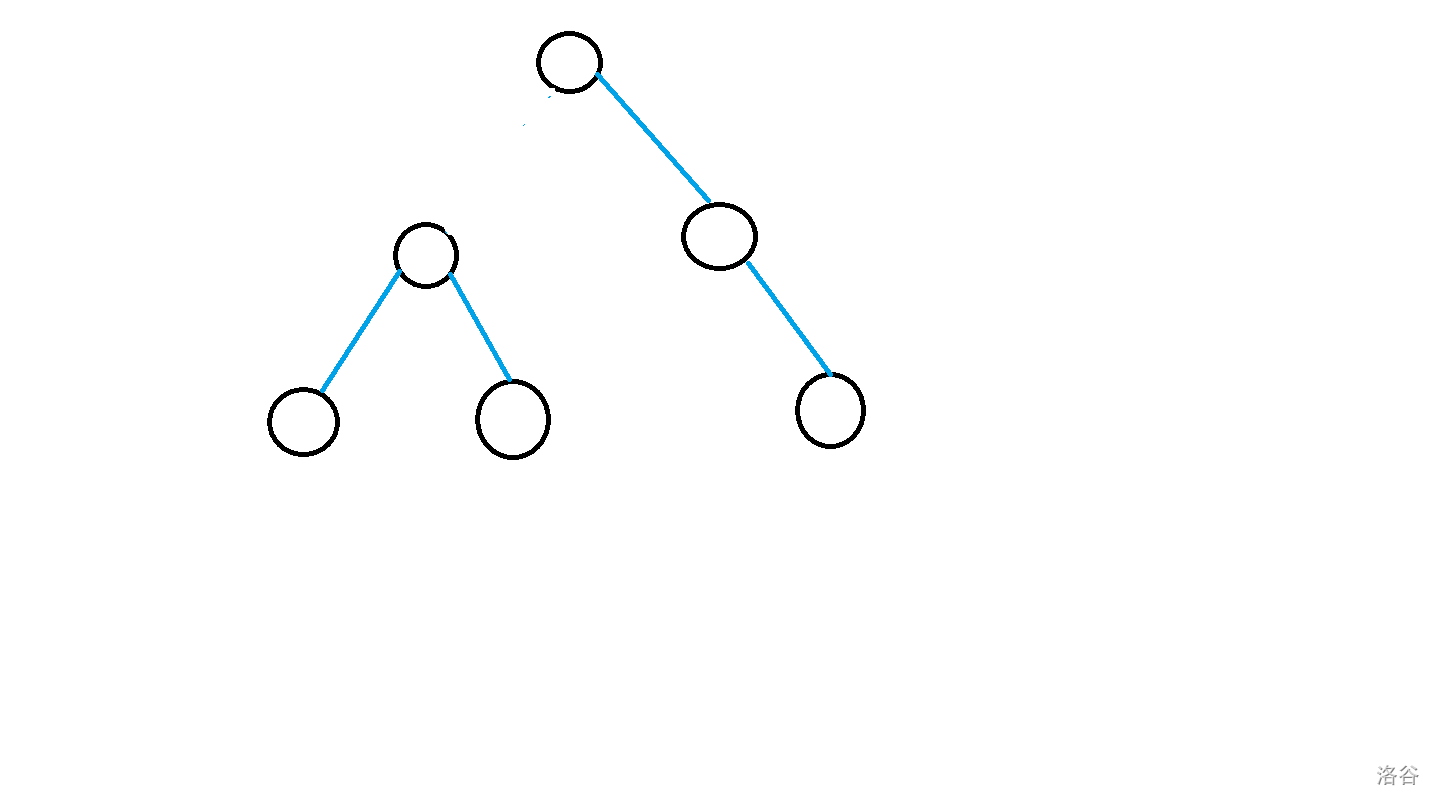
(从 ( m nofind) 大佬哪里擓来的图)
那么是不是我们只要吧原树划分成若干个互不相交的长度为 (3) 的链然后把这些点之间的边染成蓝色这样的树都是合法的呢?其实不是,比如下面这个情况:
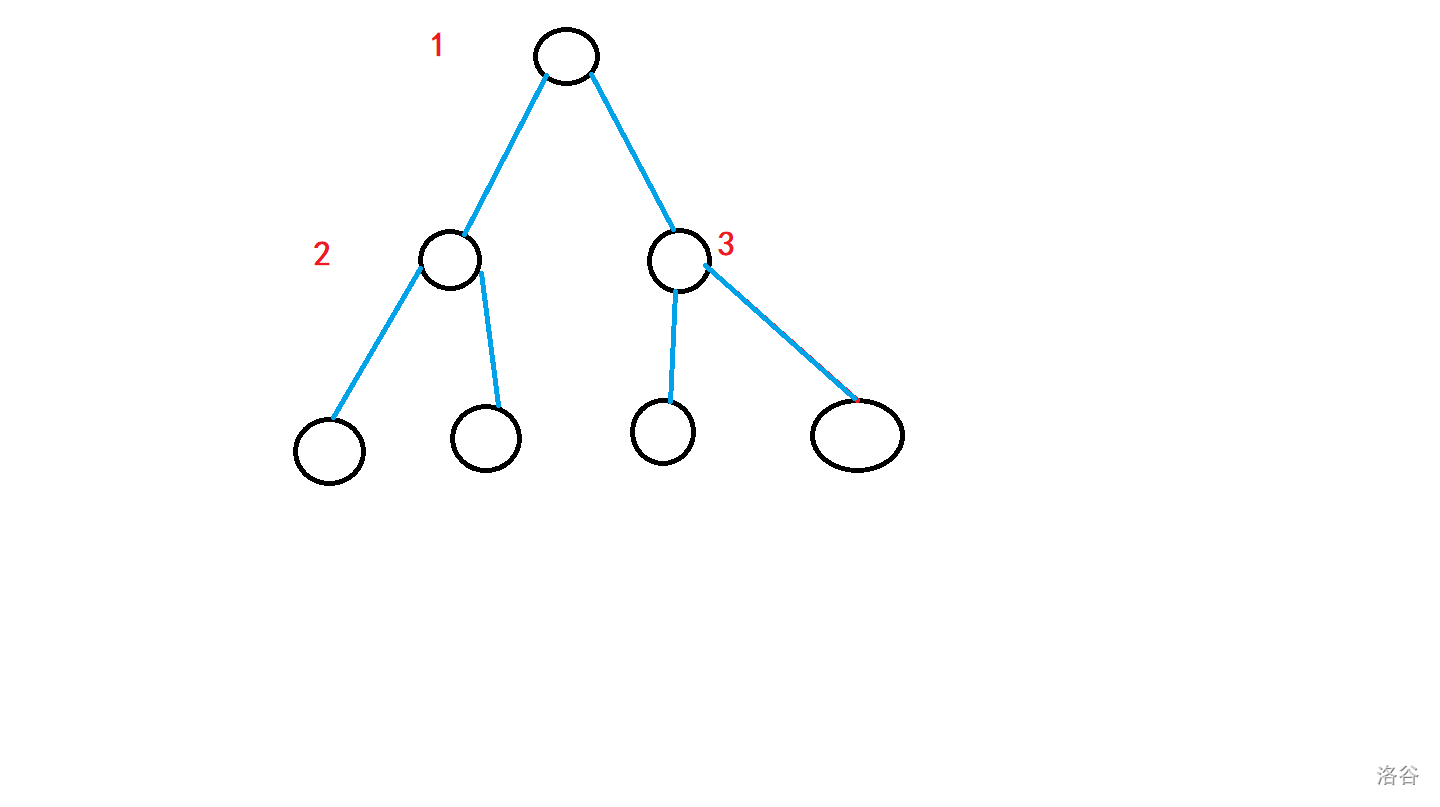
按照上面的理论,我们可以选择左下角和右下角的三个点作为蓝线所在的链,但实际上这是不可能的,因为我们只能从一个珠子开始,所以如果要选择左下角那三个点,那么必须一步步地拉红线过去,而最终一定会先拉到 (3) 号点,这样就不能先连下面两个点再让 (3) 成为中间的的连接点。于是我们可以发现一个划分蓝边的方案是合法的当且仅当向前面提到的第一种长度为 (3) 的链的中间点都在同一条链上,第二种长度为 (3) 的链随意。那么最终划分出来的蓝色的链大致就是下面这个模样:
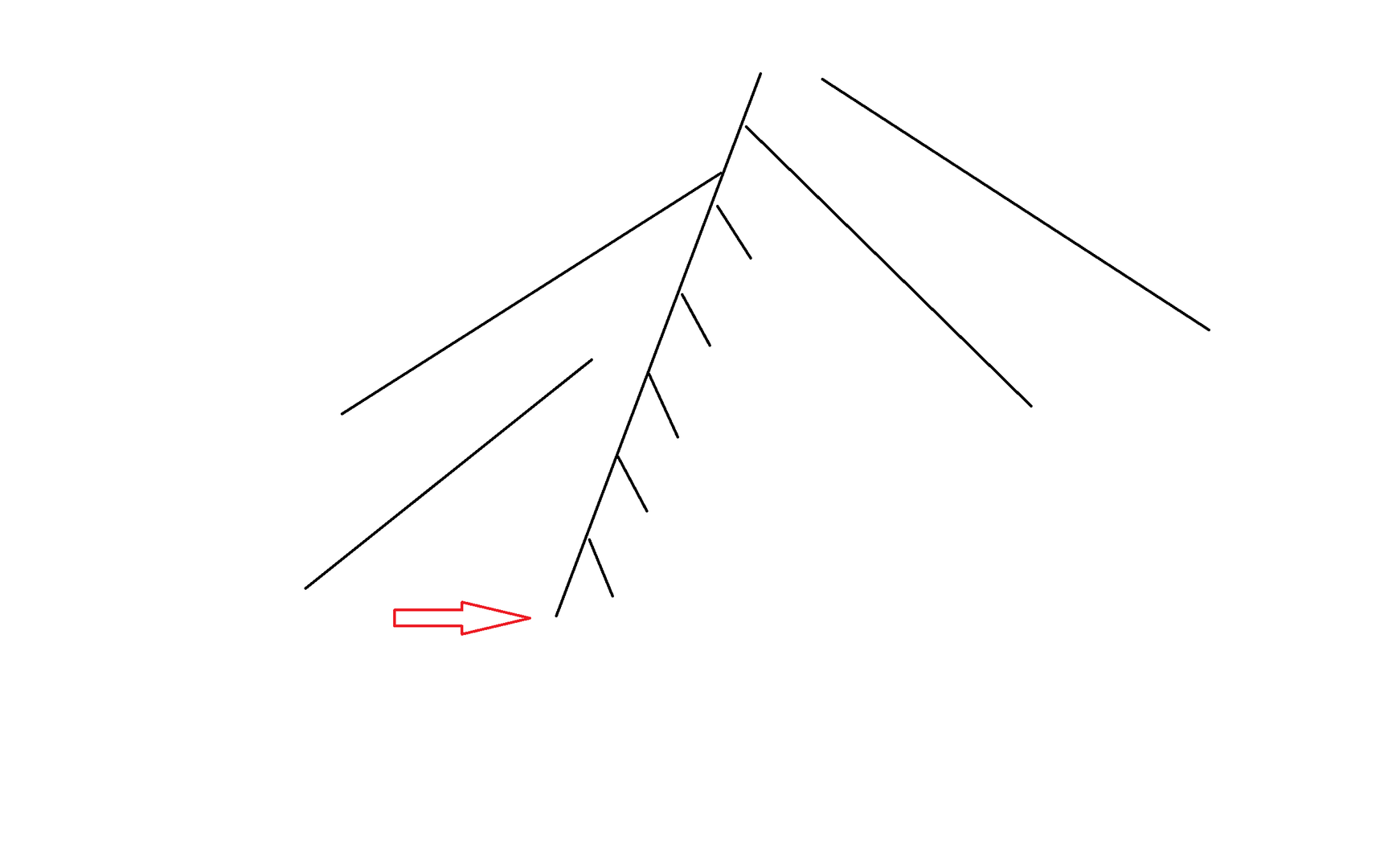
可以感觉到这个东西是不能贪心求解最优解的,那么我们只能考虑 (dp) 了,但是如果我们要直接去做的话不仅状态很难设计,转移也非常繁杂。为了简化状态,一个常见的想法就是看能否将上面的两种划分方式看成一种,不难发现第二种划分方案是更好来做的,于是我们可以考虑将第一种划分方案转化成第二种划分方案。观察一下这条链,第一种划分方案实际上是儿子 ( ightarrow) 父亲 ( ightarrow) 儿子,那么我们只需要在上面红色箭头指向的点做为树的根将树倒过来,那么原来的儿子 ( ightarrow) 父亲 ( ightarrow) 儿子,就会变成儿子 ( ightarrow) 父亲 ( ightarrow) 爷爷了。那么我们只需要枚举每个根,然后做一遍只能是第二种划分 (dp) 即可。再来考虑这个只能是第二种划分的 (dp),可以发现当前的点有三种划分方案:不和任何点划分在一起,和一个儿子划分在一起,和父亲划分在一起。但是我们可以发现这三种状态中对父亲的影响只有两种:父亲必须和它划分在一起,即它选择了和儿子的一条边;父亲不一定要与它划分在一起。不难发现这两种状态的本质不同在于这个点是否恰好与儿子连了一条边(即这个集合还需要假如父亲),于是我们可以根据这个设计状态。令 (dp_{i, 0 / 1}) 表示 (i) 是否恰好与儿子连了一条边。那么就有转移:
这样就可以做到 (O(n ^ 2)) 了,当要枚举不同的根时一个常见的套路就是使用换根 (dp),让我们来思考一下从 (u) 为根到 (v) 为根需要变换那些值。首先这里换根时影响到的 (dp) 值实际上只有 (u, v) 两个节点。(dp_{u, 0}) 只需减去 (max{dp_{v, 0}, dp_{v, 1} + e_i.w}) 即可。(dp_{u, 1}) 的变化比较麻烦,因为可能出现 (dp_{u, 1}) 是从 (v) 转移过来的情况,这样 (v) 对答案的影响就可能有两种,但我们可以提前预处理好 (f_v) 表示在以 (fa_v) 为根的子树内出去 (v) 的 (dp_{fa_v, 1}) 的值,具体地我们只需在最初每次转移时记录最大值和次大值即可。但要注意的是每次在换根的时候 (f_v) 是会改变的,因此换根是我们还需再次 (dp) 一边,然后使用栈记录原来的 (dp) 值,结束换根后还原即可。对于 (dp_{v, 0}) 的更新,只需加上 (max{dp_{u, 0}, dp_{u, 1} + e_i.w}) 即可;对于 (dp_{v, 1}) 的更新,将原来的树中的最优点点的答案和 (u) 这个点最为最优点时的答案比较即可。
#include<bits/stdc++.h>
using namespace std;
#define rep(i, l, r) for(int i = l; i <= r; ++i)
#define Next(i, u) for(int i = h[u]; i; i = e[i].next)
const int N = 200000 + 5;
const int inf = 2000000000;
struct edge{
int v, next, w;
}e[N << 1];
long long ans, f[N], st[N], dp[N][2];
int n, u, v, w, tot, top, h[N];
int read(){
char c; int x = 0, f = 1;
c = getchar();
while(c > '9' || c < '0'){ if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
void add(int u, int v, int w){
e[++tot].v = v, e[tot].w = w, e[tot].next = h[u], h[u] = tot;
e[++tot].v = u, e[tot].w = w, e[tot].next = h[v], h[v] = tot;
}
void dfs1(int u, int fa){
dp[u][0] = 0;
Next(i, u){
int v = e[i].v; if(v == fa) continue;
dfs1(v, u), dp[u][0] += max(dp[v][0], dp[v][1] + e[i].w);
}
long long mx = -inf, se = -inf, tmp, p = 0;
Next(i, u){
int v = e[i].v; if(v == fa) continue;
tmp = dp[u][0] - max(dp[v][0], dp[v][1] + e[i].w) + dp[v][0] + e[i].w;
if(tmp > mx) se = mx, mx = tmp, p = v;
else if(tmp > se) se = tmp;
}
dp[u][1] = mx;
Next(i, u){
int v = e[i].v; if(v == fa) continue;
f[v] = (p == v ? se : mx);
}
}
void dfs2(int u, int fa){
ans = max(ans, dp[u][0]);
Next(i, u){
int v = e[i].v; if(v == fa) continue;
long long fdp0 = dp[u][0], fdp1 = dp[u][1], sdp0 = dp[v][0], sdp1 = dp[v][1];
dp[u][0] -= max(dp[v][0], dp[v][1] + e[i].w);
dp[u][1] = f[v] - max(dp[v][0], dp[v][1] + e[i].w);
dp[v][0] += max(dp[u][0], dp[u][1] + e[i].w);
dp[v][1] = max(dp[v][1] + max(dp[u][0], dp[u][1] + e[i].w), sdp0 + dp[u][0] + e[i].w);
int fir = top;
Next(j, v){
int nxt = e[j].v; if(nxt == v) continue;
st[++top] = f[nxt], f[nxt] = max(f[nxt] + max(dp[u][0], dp[u][1] + e[i].w), dp[u][0] + e[i].w + sdp0);
}
dfs2(v, u), dp[u][0] = fdp0, dp[u][1] = fdp1, dp[v][0] = sdp0, dp[v][1] = sdp1;
reverse(st + fir + 1, st + top + 1);
Next(j, v) if(e[j].v != v) f[e[j].v] = st[top--];
}
}
int main(){
n = read();
rep(i, 1, n - 1) u = read(), v = read(), w = read(), add(u, v, w);
dfs1(1, 0), dfs2(1, 0);
printf("%lld", ans);
return 0;
}