动态规划算法

一、斐波那契数列（递推思想，动态规划算法）

二、多源最短路径（给定带权有向图（G = （V，E）），求任意两顶点（Vi，Vj）之间的最短路径）

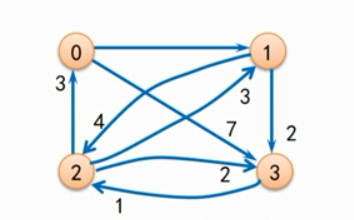
　　弗洛伊德算法（Floyd），动态规划思想，算法复杂度大O（N的三次方）。

　　算法步骤：

　　1、先定义一个n阶的矩阵，令其对角线的值为0，若存在弧，则对应元素为弧值，否则为无穷大

　　2、逐步在原直接路径中增加中间顶点，若加入中间顶点后，路径变短，则修改之，否则维持

　　3、所有顶点试探完毕，算法结束。

#include <stdio.h>
#include<stack>
#define N 4
#define MAXINT 1000
int main()
{    
    //#ifndef N
    int i,j,k;
    /* 
       1.A数组, 存储顶点之间弧值,对角线值为0,
       顶点之间存在弧,存弧值,否则弧值MAXINT       
    */
    int A[N][N] = {   0,      5,      MAXINT,  7,
                      MAXINT, 0,      4,       2,
                      3,      3,      0,       2,
                      MAXINT, MAXINT, 1,       0    
                  };
                  
    /* 2.D数组Path数组赋值 */               
    int D[N][N];    //Vi到Vj的最短路径长度
    int Path[N][N]; //Vi到Vj的最短路径

    for(i=0; i<N; ++i)
    {
        for(j=0; j<N; ++j)
        {
            /* D数组赋值 */
            D[i][j] = A[i][j]; 
            /* Path数组赋值 */
            if(i!=j && A[i][j] < MAXINT) 
                Path[i][j] = i;
            else 
                Path[i][j] = -1;
        }
    }
    
    /* 3.计算最短路径长度及最短路径 */    
    //加入k顶点的最短路径长度
    //D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
    for(k=0; k<N; k++)
    {
        for(i=0; i<N; i++)
        {
            for(j=0; j<N; ++j)
            {
                if(D[i][k]+D[k][j] < D[i][j]){
                    D[i][j] = D[i][k] + D[k][j];
                    Path[i][j] = Path[k][j];
                }
            }
        }
    } 
    //#endif
    
    /* 4.打印最短路径长度 */
    for(i=0; i<N; ++i){
        for(j=0; j<N; ++j)
            printf("%5d",D[i][j]);
        printf("
");
    }
    printf("
");
    /* 
        0  5  8  7
        6  0  3  2
        3  3  0  2
        4  4  1  0
    */
    
    /* 5.打印最短路径路径 */
    for(i=0; i<N; ++i){
        for(j=0; j<N; ++j)
            printf("%5d",Path[i][j]);
        printf("
");
    }
    printf("
");
    /* 
       -1  0  3  0
        2 -1  3  1
        2  2 -1  2
        2  2  3 -1
    */
    
    /* 6.打印顶点1到顶点0的最短路径 */
    int v1 = 1,v0 = 0;
    
    /* int arr[N] = {v0}, index = 1;
    while(Path[v1][v0] != -1){
        arr[index++] = v0 = Path[v1][v0];        
    }
        
    for(int i=index-1; i>=0; --i){
        if(i != index-1) printf(" ->");
        printf(" %d",arr[i]);
    }*/
    /* 1 -> 3 -> 2 -> 0 */
        
    printf("%5d",v0);
    while(Path[v1][v0] != -1)
    {
        printf(" <- %d",Path[v1][v0]);
        v0 = Path[v1][v0];    
    }
    printf("
"); 
    /* 0 <- 2 <- 3 <- 1 */    
    return 0;
}