定义
(1)堆是一个完全二叉树。(除了叶子节点,其他节点的值都是满的)
(2)堆中每一个节点的值都必须大于等于(或者小于等于)其左右节点的值。 对于每个节点的值大于等于子树的值,称为大顶堆。反之称之为小顶堆。
图示(大顶堆):
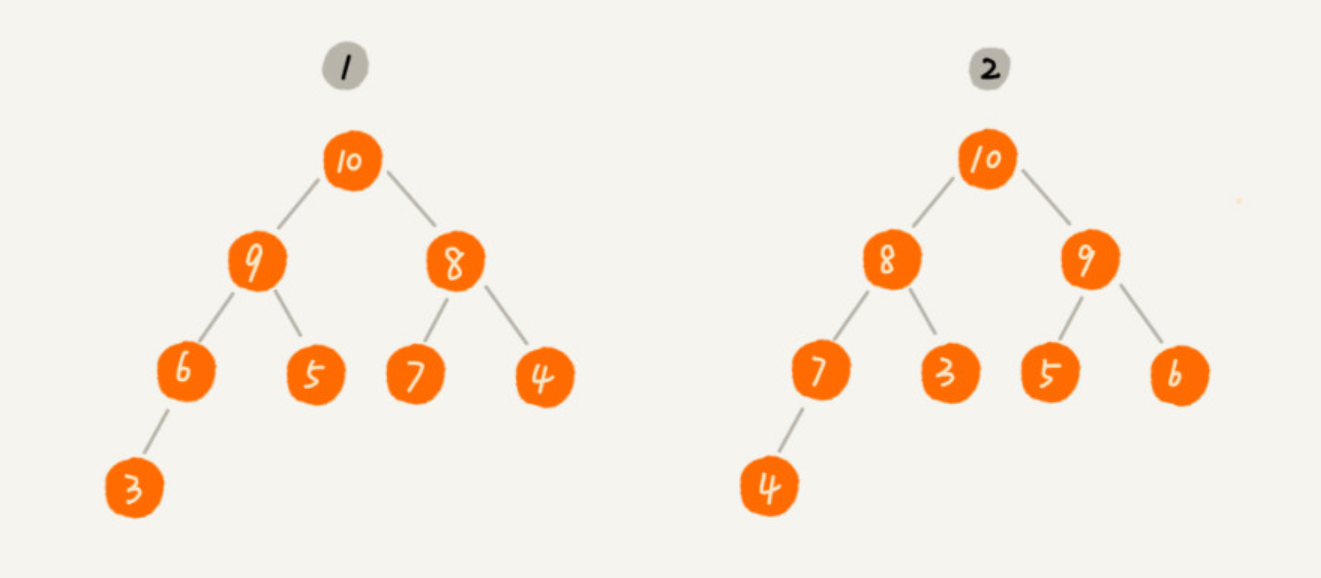
堆的实现
因为堆的执行(完全二叉树),他适合用数组直接进行存储。数组中下标为i的节点的左右节点为为i*2, i*2+1。而任意一个节点i的父节点是i/2。这里我们在平时可以选择下边1作为第一个节点,有助于理解和代码的书写。如果我们用下标0作为第一个节点的话, 其子节点为(i+1)/2 ,(i+1)/2 +1。

堆的操作
插入操作 :在向堆中插入一个数据时,我们还是需要继续满足堆的特性。我们先将数据插入到数组的尾部,然后进行调整,让其重新满足堆的特性,这个过程就叫作堆化。
堆化过程:从下往上堆化。
从下往上堆化过程:先将数据插入到数组尾部,然后比较其父节点关系,然后继续进行交换。直到最后满足堆的性质。

实现代码
1 class Heap():
2 def __init__(self, capacity): # 初始化
3 self.a = [0] * (capacity+1)
4 self.n = capacity
5 self.count = 0
6
7 def insert(self, data): # 插入操作,自下而上进行堆化
8 if self.count >= self.n: # 如果满了直接返回
9 return
10 self.count += 1 # 数量加一
11 self.a[self.count] = data # 将插入的数据添加到尾部
12 index = self.count # 记录当前下标
13 while index//2 >0 and self.a[index] > self.a[index//2]: # 堆化调整, 因为时大顶堆,所以如果子节点大于父节点应该交换,比记录父节点的下标。
14 self.a[index], self.a[index//2] = self.a[index//2], self.a[index]
15 index = index // 2
16
删除操作:在堆中我们一般都是删除堆顶的元素,很少删除指定下标节点的情况。所以我们还是只讨论对于堆顶元素的删除情况。
堆化过程:从上往下堆化。
从上到下进行堆化过程:在堆化的图示过程中我们可以看待,这种情况会导致最后完成之后不能满足完全二叉树的情况。从而也就破坏了堆的性质。
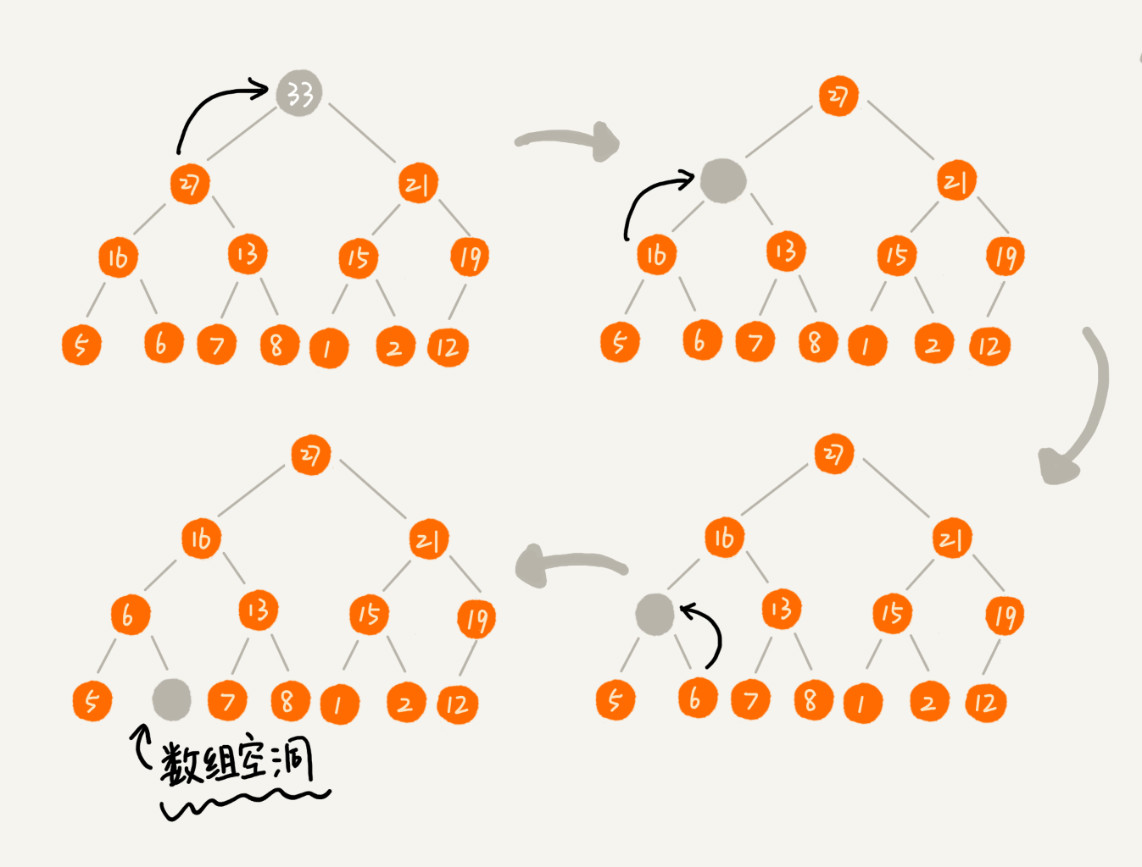
鉴于此情况,我们可以将待删除的元素和数组中最后一个元素进行对调,然后从堆顶从一次向下进行堆化,直到最后满足定义。这样完毕之后他还是满足完全二叉树的定义。图示如下:
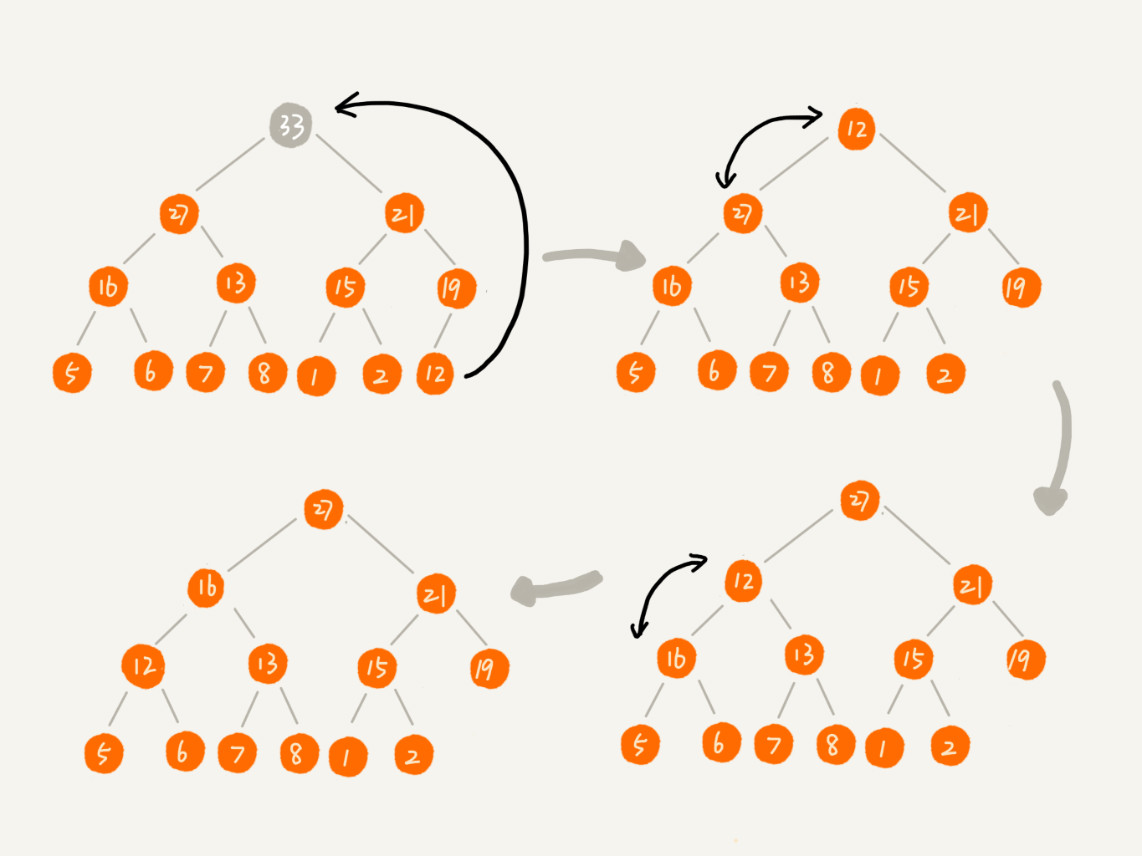
代码实现
1 def delete(self):
2 if self.count == 0:
3 return
4 self.a[1], self.a[self.count] = self.a[self.count], self.a[1] # 先交换最后一个和起始元素的位置
5 self.count -= 1 # 数量减一
6 tem = 1 # 第一个节点下标
7 while True:
8 index = tem # 记录下标
9 if tem*2 <= self.count and self.a[tem] < self.a[tem*2]: # 下面这两个判断主要是在tem的左右节点中选择一个最小的继续交换。
10 index = tem *2
11 if tem*2+1 <= self.count and self.a[index] < self.a[tem*2+1]:
12 index = tem * 2+1
13 if index == tem: # 没有发生交换,循环结束
14 break
15 self.a[tem], self.a[index] = self.a[index], self.a[tem] # 交换位置
16 tem = index # 从当前下标继续开始
复杂度分析:在对对进行操作时都不需要申请辅助空间,所以其空间复杂度为O(1),而对于时间复杂度,由于是以完全二叉树的性质进行存储的,从根节点到叶子节点的高度为log n ,因此在堆化的过程中时间,无论是插入操作还是删除操作其时间复杂度为O(log n)。