2020 Multi-University Training Contest 4

1007.Go Running

题目连接

大致题意：

一群人在数轴上跑步 ，匀速1m/s ，起点终点都随意， 可以从左往右跑 也可以 从右往左跑 ， 给你 n 个信息：

可以确定在 t[ i ] 秒 时在坐标 x[ i ] 的位置上至少有一个人

问： 至少有几个人在跑步？

思路:

首先 : 

　　把x作为一个坐标轴，t作为一个坐标轴，形成二维平面，那么每个信息（每个（t[ i ] , x[ i ] ）） 就是平面上的一个点

　　

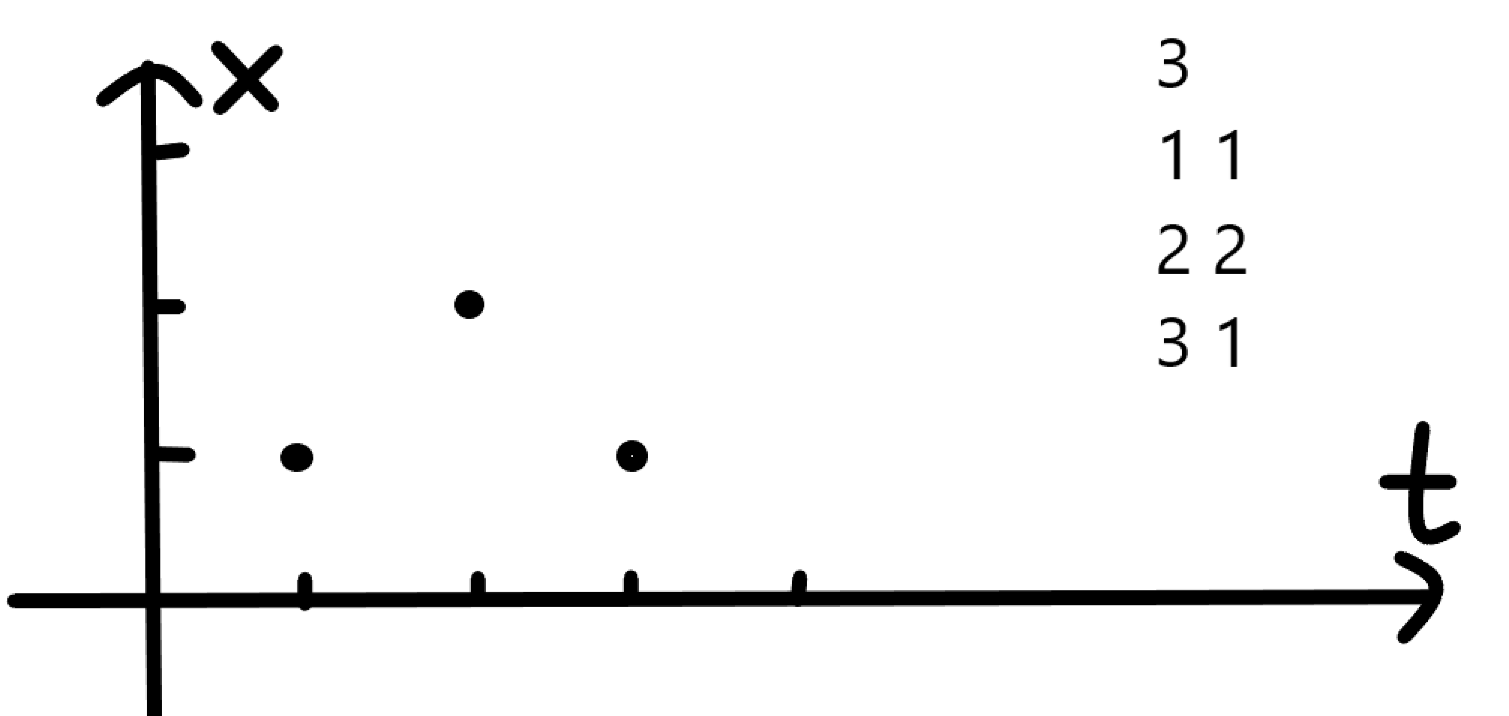
　　由于每个人跑步的速度都是 1 m / s ，所以每个人的轨迹是类似这样的：

   

  

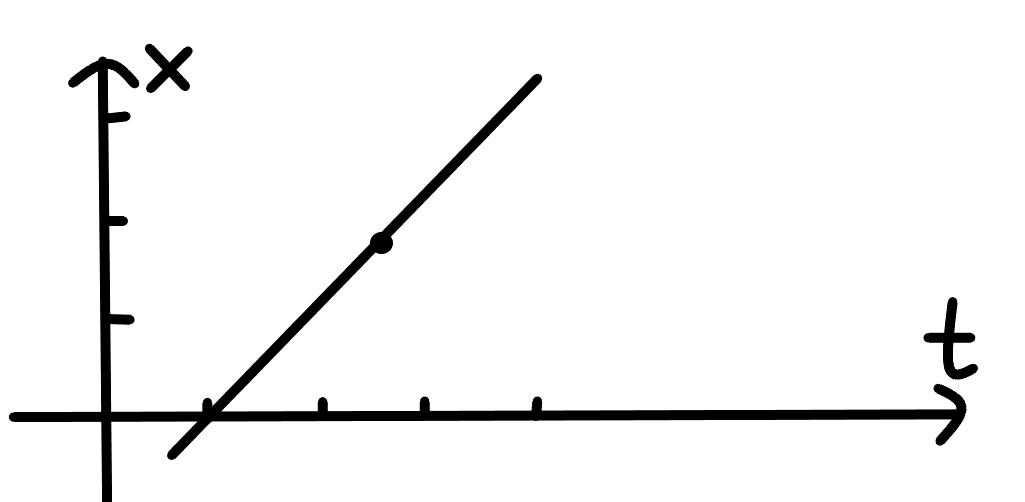
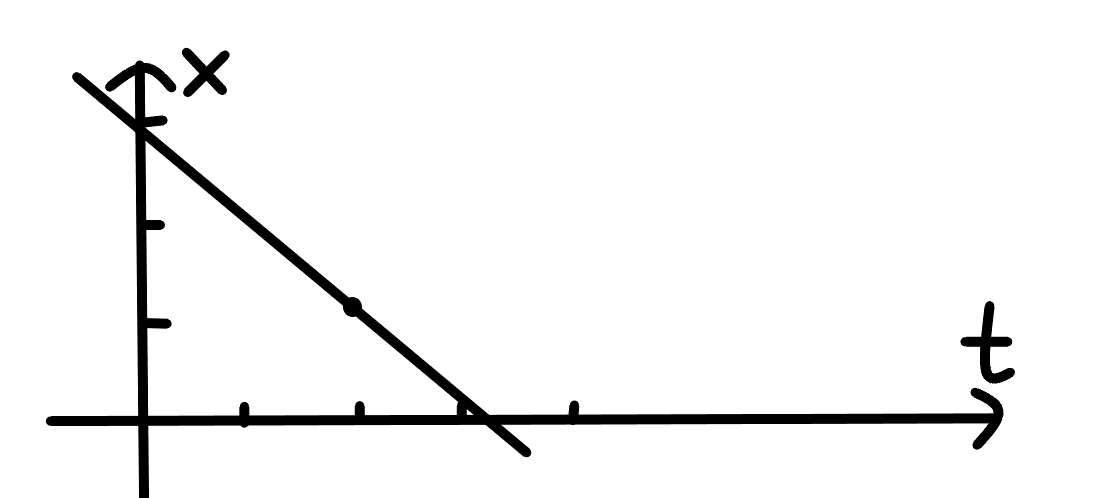
当我们规定从左往右跑是正方向的时候 ，前面的图就是从左往右跑，后面的图就是从右往左跑。

所以问题变成了 ： 至少要使用多少条直线（斜率为1或者-1），才能覆盖图上所有的点 ？

例如这个样例:

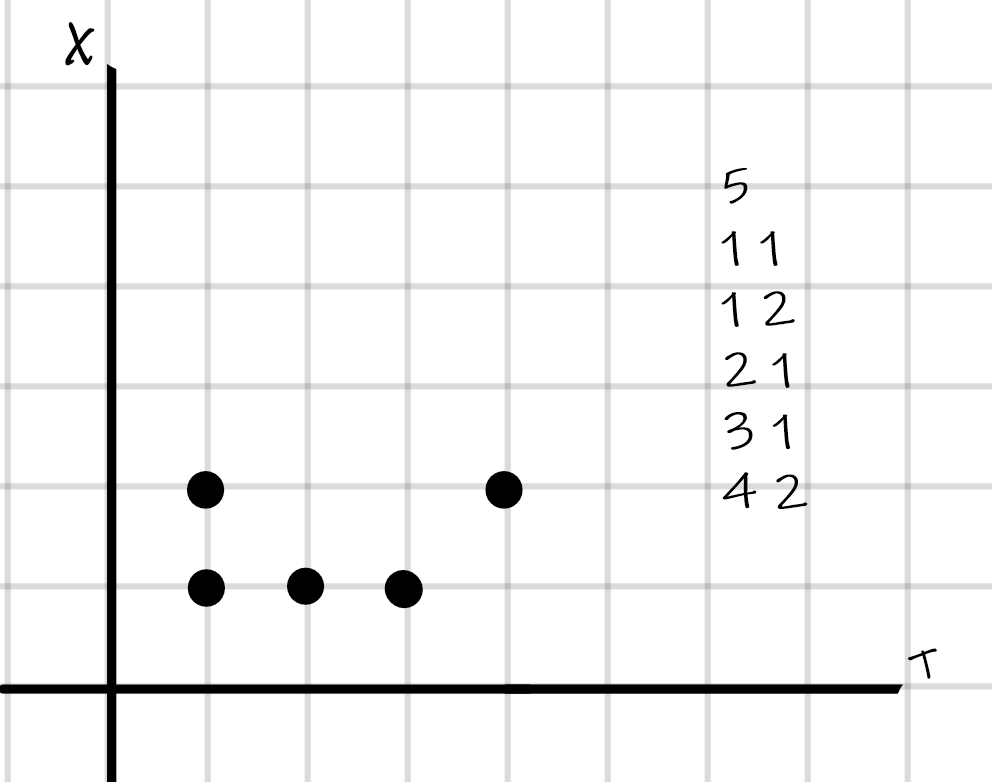
 答案是3，其中一种选取方式是这样的：

 

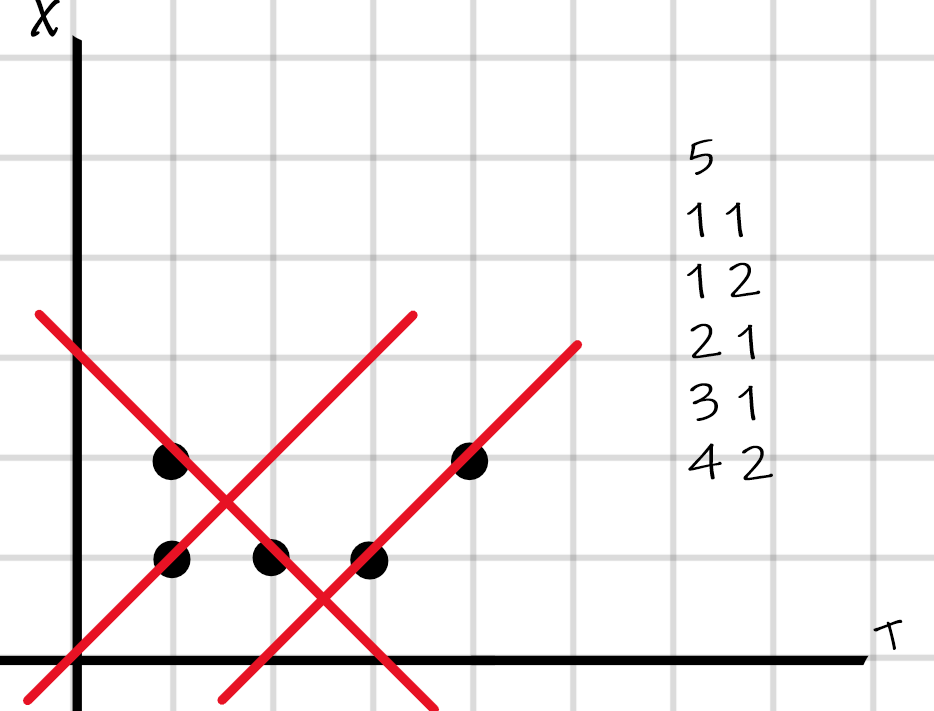
 把他旋转一下

 

修改一下坐标轴：

 于是问题就变成了：  至少要使用多少条 平行于x轴 或 平行于y轴的 直线，才能覆盖图上所有的点 ？

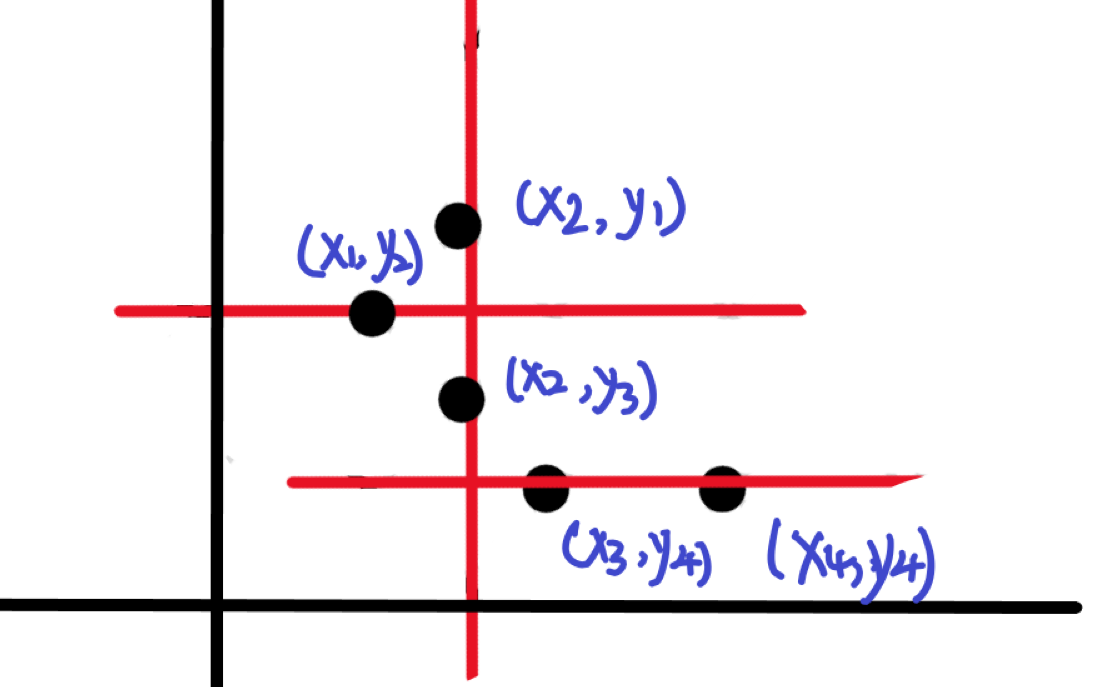
标上坐标，发现：只要有 x = x2 ,  y = y2 , y= y4 这三条

再来改变一下形状，把原本坐标上的点变成一条线。

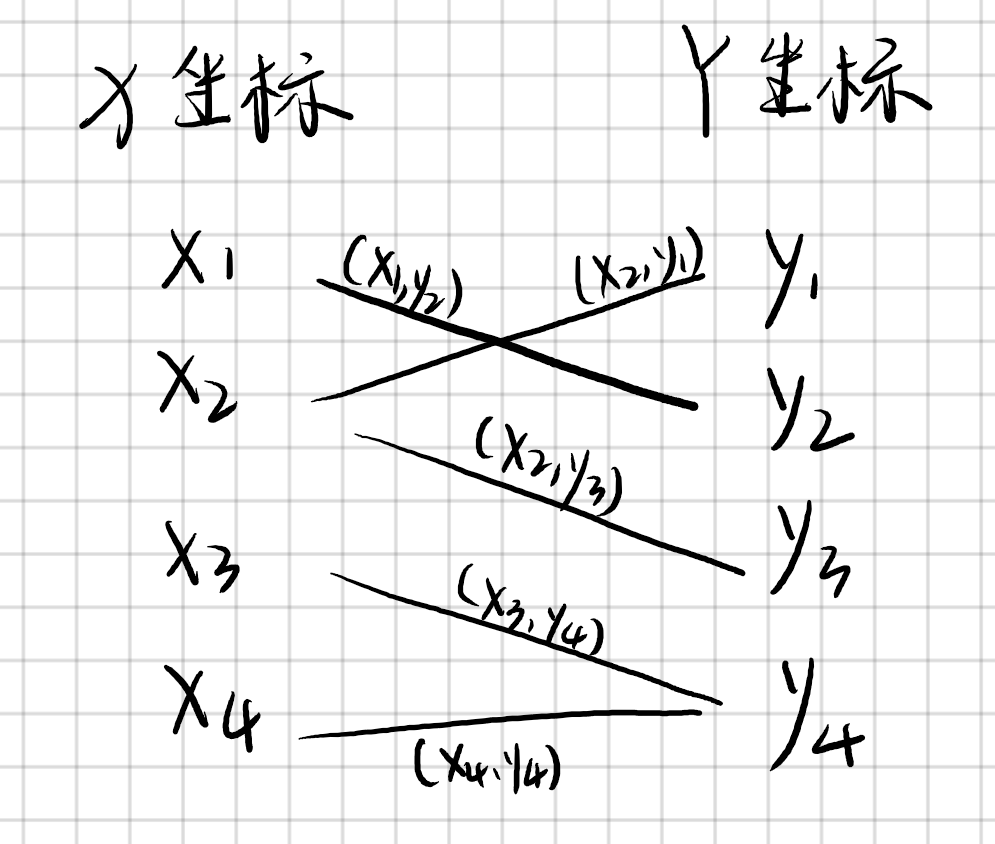
问题就变成了：要选取最少的 多少个 点x 和 点y，可以把所有的边都覆盖，也就是 二分图的最小点覆盖。

又：最小点覆盖数 = 最大匹配数 ， 所以答案就是 二分图的最大匹配。

由于数据太大了 ， n有1e5 ， 二分图容易超时 ，所以改用最大流来计算二分图的最大匹配。

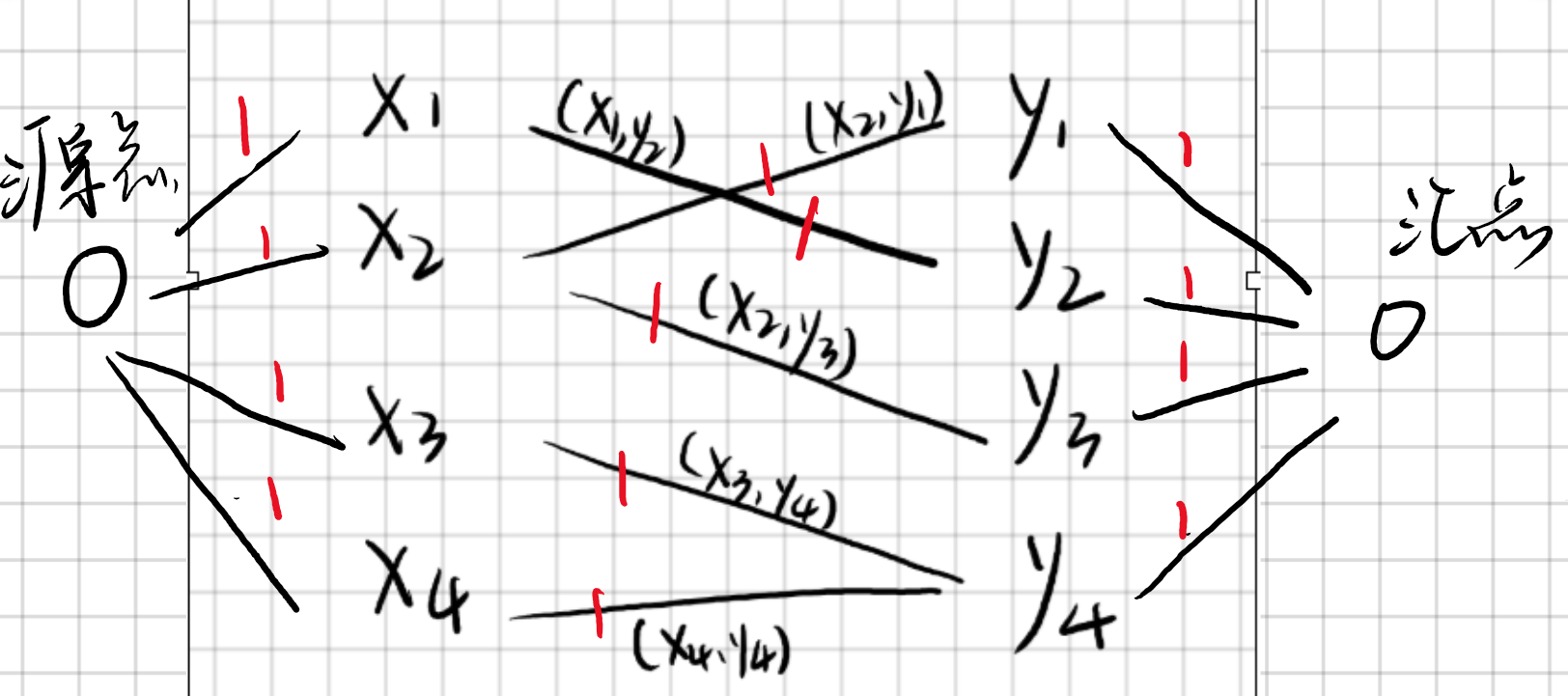
 问题就变成了：如图所示的最大流是多少（两点之间的流量是1）。

所以按照输入构建一个图算流量就好了。

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn =  2e5 + 10;
#define ll long long
#define ios std::ios::sync_with_stdio(false)
const ll INF(0x3f3f3f3f3f3f3f3fll);
const int inf(0x3f3f3f3f);
#define int long long
#define pb(a) push_back(a)
#define debug(a) cout << "a : " << a << '
'
#define mp(a , b) make_pair(a ,b)
const int mod = 998244353;
const double eps = 1e-6;
template<typename T>void read(T &res){bool flag=false;char ch;while(!isdigit(ch=getchar()))(ch=='-')&&(flag=true);
for(res=ch-48;isdigit(ch=getchar());res=(res<<1)+(res<<3)+ch - 48);flag&&(res=-res);}
template<typename T>void Out(T x){if(x<0)putchar('-'),x=-x;if(x>9)Out(x/10);putchar(x%10+'0');}
#define sb cout << "sbsb
";
struct node{
    int u , v , cap , flow;
    node(){}
    node(int u , int v , int cap , int flow){
        this -> u = u , this -> v = v , this -> cap = cap , this -> flow = flow;
    }
};
vector<node>G;
vector<int>id[maxn];
int n , m , st , ed , dis[maxn] , vis[maxn];
queue <int> que;
void add(int u , int v , int w)
{
    G.push_back(node(u , v , w , 0));
    G.push_back(node(v , u , 0 , 0));
    int sz = G.size();
    id[u].pb(sz - 2) , id[v].pb(sz - 1);
}
bool bfs()
{
    for(int i = 0 ; i <= ed ; i ++) dis[i] = INF , vis[i] = 0;
    dis[st] = 0;
    vis[st] = 1;
    que.push(st);
    while(!que.empty())
    {
        int u = que.front();
        que.pop();
        for(auto i : id[u])
        {
            node v = G[i];
            if(v.cap-v.flow > 0 && !vis[v.v])
            {
                dis[v.v] = dis[u] + 1 , vis[v.v] = 1;
                que.push(v.v);
            }
        }
    }
    if(vis[ed]) return 1;
    return 0;
}
int dfs(int u , int w)
{
    int flow = 0 , R = 0;
    if(u == ed || w == 0) return w;
    for(int i = 0 ; i < id[u].size(); i++)
    {
        node &v = G[id[u][i]];
        if(dis[v.v] == dis[u] + 1 && (R = dfs(v.v , min(v.cap - v.flow , w))) > 0)
        {
            flow += R;
            G[id[u][i]].flow += R;
            G[id[u][i]^1].flow -= R;
            w -= R;
            if(!w) break;
        }
    }
    return flow;
}
int dinic()
{
    int flow = 0;
    while(bfs()) flow += dfs(st , INF);
    return flow;
}

int x[maxn] , y[maxn];
map<int , int> ma , mb;
void init()
{
    G.clear();
    for(int i = 0 ; i <= ed ; i ++) id[i].clear();
    ma.clear() , mb.clear();
}
signed main()
{
   // ios,cin.tie(0);
    int t;
    read(t);
    while(t --){
        int n;
        read(n);
        for(int i = 1 ; i <= n ; i ++){
            int t , tt;
            read(t);read(tt);
            x[i] = t + tt , y[i] = t - tt;
        }
        ed = 2 * n + 1;
        int cnt = 1;
        for(int i = 1 ; i <= n ; i ++){
            if(!ma[x[i]]) {
                ma[x[i]] = cnt ++;
                add(0 , ma[x[i]] , 1);
            }
        }
        for(int i = 1 ; i <= n ; i ++){
            if(!mb[y[i]]){
                mb[y[i]] = cnt ++;
                add(mb[y[i]] , ed , 1);
            }
        }
        for(int i = 1 ; i <= n ; i ++){
            add(ma[x[i]] , mb[y[i]] , 1);
        }
        Out(dinic());
        printf("
");
        init();
    }
    return 0;
}

/*
1
12
LLLLRRLRRRLL
*/

DInic模板是嫖我家小宝（biao）贝的