算法学习自:MATLAB与机器学习教学视频
1、粒子群优化算法概述
粒子群优化(PSO, particle swarm optimization)算法是计算智能领域,除了蚁群算法,鱼群算法之外的一种群体智能的优化算法,该算法最早由Kennedy和Eberhart在1995年提出的,该算法源自对鸟类捕食问题的研究。
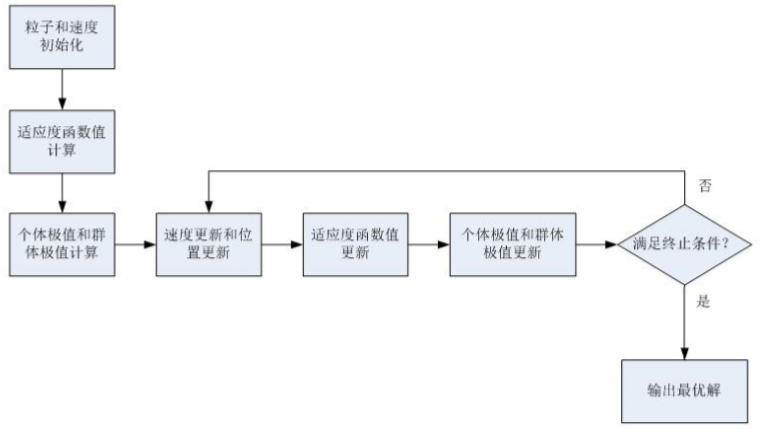
• PSO算法首先在可行解空间中初始化一群粒子,每个粒子都代表极值优化问题的一个潜在最优解,用位置、速度和适应度值三项指标表示该粒子特征。
• 粒子在解空间中运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体位置,个体极值Pbest是指个体所经历位置中计 算得到的适应度值最优位置,群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。
• 粒子每更新一次位置,就计算一次适应度值,并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体 极值Pbest和群体极值Gbest位置。
在每一次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,更新公式 如下:
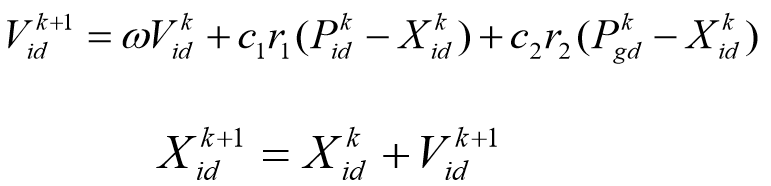
2、粒子群优化算法与遗传算法对比
• 相同点:
种群随机初始化
适应度函数值与目标最优解之间的映射
• 不同点:
PSO算法没有选择、交叉、变异等操作算子
PSO有记忆的功能
信息共享机制不同,遗传算法是互相共享信息,整个种群的移动是比较均匀地向最优区域移动,而在PSO中,只 有gBest或lBest给出信息给其他粒子,属于单向的信息流动,整个搜索更新过程是跟随当前最优解的过程。因此, 在一般情况下,PSO的收敛速度更快。
3、案例分析
①一元函数优化
在该例中,想要优化的一元函数为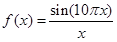 ,当x范围在[1,2],寻找它的极大值。
,当x范围在[1,2],寻找它的极大值。
matlab代码如下:

1 %% I. 清空环境 2 clc 3 clear all 4 5 %% II. 绘制目标函数曲线图 6 x = 1:0.01:2; 7 y = sin(10*pi*x) ./ x; 8 figure 9 plot(x, y) 10 hold on 11 12 %% III. 参数初始化 13 c1 = 1.49445; 14 c2 = 1.49445; 15 16 maxgen = 50; % 进化次数 17 sizepop = 10; %种群规模 18 19 Vmax = 0.5; 20 Vmin = -0.5; 21 popmax = 2; 22 popmin = 1; 23 24 %% IV. 产生初始粒子和速度 25 for i = 1:sizepop 26 % 随机产生一个种群 27 pop(i,:) = (rands(1) + 1) / 2 + 1; %初始种群 28 V(i,:) = 0.5 * rands(1); %初始化速度 29 % 计算适应度 30 fitness(i) = fun(pop(i,:)); 31 end 32 33 %% V. 个体极值和群体极值 34 [bestfitness, bestindex] = max(fitness); 35 zbest = pop(bestindex,:); %全局最佳 36 gbest = pop; %个体最佳 37 fitnessgbest = fitness; %个体最佳适应度值 38 fitnesszbest = bestfitness; %全局最佳适应度值 39 40 %% VI. 迭代寻优 41 for i = 1:maxgen 42 43 for j = 1:sizepop 44 % 速度更新 45 V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:)); 46 V(j,V(j,:)>Vmax) = Vmax; 47 V(j,V(j,:)<Vmin) = Vmin; 48 49 % 种群更新 50 pop(j,:) = pop(j,:) + V(j,:); 51 pop(j,pop(j,:)>popmax) = popmax; 52 pop(j,pop(j,:)<popmin) = popmin; 53 54 % 适应度值更新 55 fitness(j) = fun(pop(j,:)); 56 end 57 58 for j = 1:sizepop 59 % 个体最优更新 60 if fitness(j) > fitnessgbest(j) 61 gbest(j,:) = pop(j,:); 62 fitnessgbest(j) = fitness(j); 63 end 64 65 % 群体最优更新 66 if fitness(j) > fitnesszbest 67 zbest = pop(j,:); 68 fitnesszbest = fitness(j); 69 end 70 end 71 yy(i) = fitnesszbest; 72 end 73 74 %% VII. 输出结果并绘图 75 [fitnesszbest zbest]; 76 plot(zbest, fitnesszbest,'r*') 77 78 figure 79 plot(yy) 80 title('最优个体适应度','fontsize',12); 81 xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

1 function y = fun(x) 2 % 函数用于计算粒子适应度值 3 %x input 输入粒子 4 %y output 粒子适应度值 5 y = sin(10 * pi * x) / x;
结果图示:
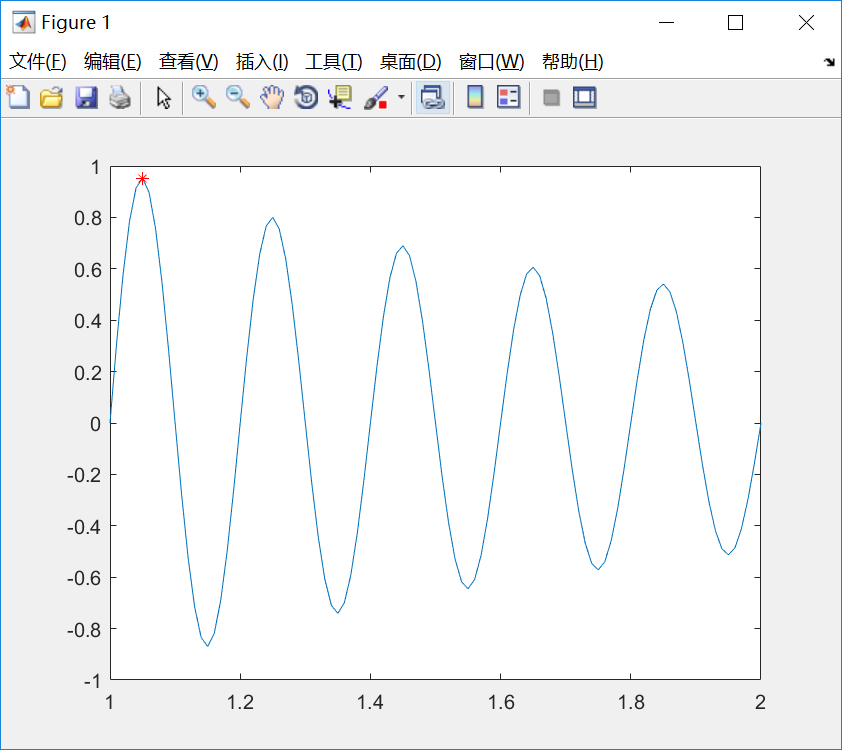

2、二元函数优化
在该例中,想要优化的二元函数为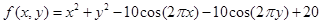 ,当x和y范围都在[-5,5],寻找它的极大值。
,当x和y范围都在[-5,5],寻找它的极大值。
matlab代码如下:

1 function y = fun(x) 2 %函数用于计算粒子适应度值 3 %x input 输入粒子 4 %y output 粒子适应度值 5 y = x(1).^2 + x(2).^2 - 10*cos(2*pi*x(1)) - 10*cos(2*pi*x(2)) + 20;

1 %% I. 清空环境 2 clc 3 clear 4 5 %% II. 绘制目标函数曲线 6 figure 7 [x,y] = meshgrid(-5:0.1:5,-5:0.1:5); 8 z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20; 9 mesh(x,y,z) 10 hold on 11 12 %% III. 参数初始化 13 c1 = 1.49445; 14 c2 = 1.49445; 15 16 maxgen = 1000; % 进化次数 17 sizepop = 100; %种群规模 18 19 Vmax = 1; 20 Vmin = -1; 21 popmax = 5; 22 popmin = -5; 23 24 %% IV. 产生初始粒子和速度 25 for i = 1:sizepop 26 % 随机产生一个种群 27 pop(i,:) = 5*rands(1,2); %初始种群 28 V(i,:) = rands(1,2); %初始化速度 29 % 计算适应度 30 fitness(i) = fun(pop(i,:)); %染色体的适应度 31 end 32 33 %% V. 个体极值和群体极值 34 [bestfitness bestindex] = max(fitness); 35 zbest = pop(bestindex,:); %全局最佳 36 gbest = pop; %个体最佳 37 fitnessgbest = fitness; %个体最佳适应度值 38 fitnesszbest = bestfitness; %全局最佳适应度值 39 40 %% VI. 迭代寻优 41 for i = 1:maxgen 42 43 for j = 1:sizepop 44 % 速度更新 45 V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:)); 46 V(j,find(V(j,:)>Vmax)) = Vmax; 47 V(j,find(V(j,:)<Vmin)) = Vmin; 48 49 % 种群更新 50 pop(j,:) = pop(j,:) + V(j,:); 51 pop(j,find(pop(j,:)>popmax)) = popmax; 52 pop(j,find(pop(j,:)<popmin)) = popmin; 53 54 % 适应度值更新 55 fitness(j) = fun(pop(j,:)); 56 end 57 58 for j = 1:sizepop 59 % 个体最优更新 60 if fitness(j) > fitnessgbest(j) 61 gbest(j,:) = pop(j,:); 62 fitnessgbest(j) = fitness(j); 63 end 64 65 % 群体最优更新 66 if fitness(j) > fitnesszbest 67 zbest = pop(j,:); 68 fitnesszbest = fitness(j); 69 end 70 end 71 yy(i) = fitnesszbest; 72 end 73 %% VII.输出结果 74 [fitnesszbest, zbest] 75 plot3(zbest(1), zbest(2), fitnesszbest,'bo','linewidth',1.5) 76 77 figure 78 plot(yy) 79 title('最优个体适应度','fontsize',12); 80 xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
结果图示:

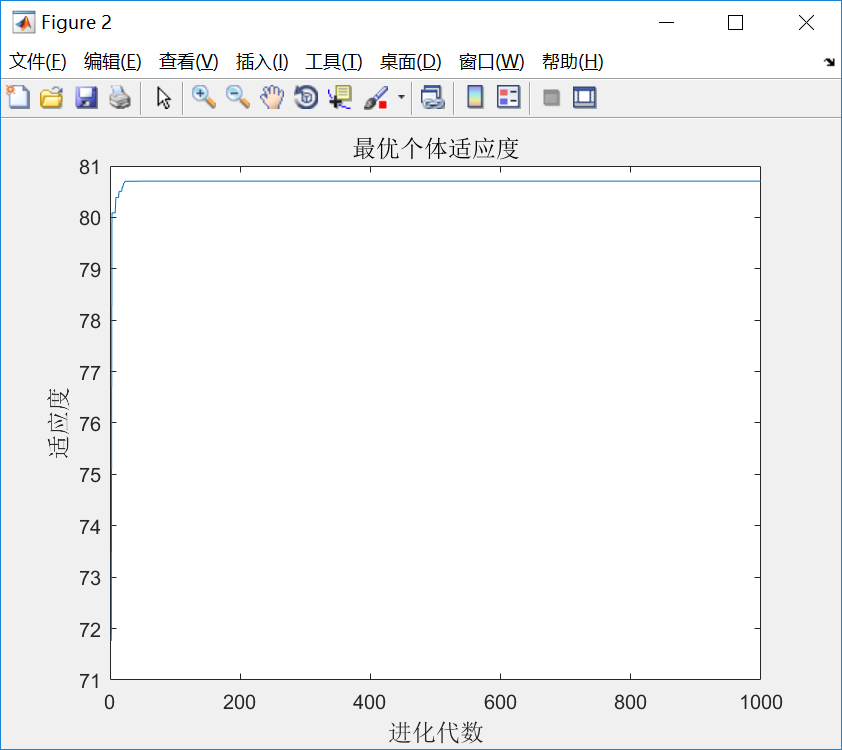
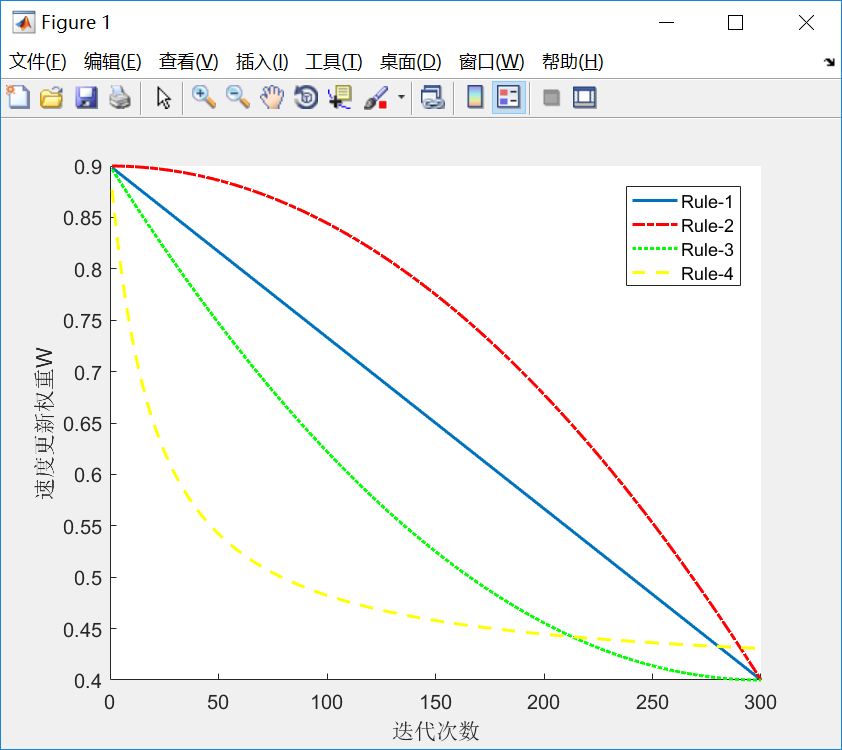
4、速度更新权重W的选择
示例代码如下:

1 ws = 0.9; 2 we = 0.4; 3 maxgen = 300; 4 hold on; 5 6 for k = 1:maxgen 7 w(k) = ws - (ws-we)*(k/maxgen); 8 end 9 plot(w,'linewidth',1.5); 10 11 for k = 1:maxgen 12 w(k) = ws - (ws-we)*(k/maxgen)^2; 13 end 14 plot(w,'r-.','linewidth',1.5); 15 16 for k = 1:maxgen 17 w(k) = ws - (ws-we)*(2*k/maxgen-(k/maxgen)^2); 18 end 19 plot(w,'g:','linewidth',1.5); 20 21 for k = 1:maxgen 22 w(k) = we * (ws/we)^(1/(1+10*k/maxgen)); 23 end 24 plot(w,'y--','linewidth',1.5); 25 26 legend('Rule-1','Rule-2','Rule-3','Rule-4') 27 xlabel('迭代次数') 28 ylabel('速度更新权重W')
图示: