以下问题均允许离线,根节点都为1。
prob1 : 一棵有根树,要求线性时间求出任意子树的权值和。
prob2 : 一颗有根树,要求O(nlogn)求出与u距离不超过x且在u子树中的节点的权值和。
prob3 : 一颗有根树,要求O(nlogn)求出与u距离不超过x且在u子树中的不同颜色种类个数,颜色数不超过1E6。
prob4 : 一颗有根数,要求O(nlogn+大常数)求出与u距离不超过x且在u子树中的权值的lcm取模,节点的值不超过1E6,质因子不超过1E4。TIPS:取模后传统公式显然不成立。
(未填完)
Prob 1
这个问题很简单吧,找个dfs序做个前缀和就可以了。
但是dfs序却是很有用的。
没有代码。
Prob 2
有了限制,但我们注意到这个问题只是询问某个节点往下深度不超过x的权值和。
沿用prob1的思想,我们仍然想用前缀和,而一个节点的贡献与他的深度有关。
因此我们以深度为下标,按照dfs序依次加入可持久化线段树中,就能计算答案了。
实现太简单,没有代码。
Prob 3
树的问题太难了,我们先想链上问题怎么做。
现在问题的关键在于,会有重复的计数,因此我们要消除这个影响。
将询问离线下来,按照询问右端点排序,依次加入每一个点。若该点与前面有重复的,在前面的位置上减去1的贡献。
这样就转换为单点修改,区间查询,树状数组即可。
树上也同样,先求出dfs序,将询问按deppos+x排序,再依次加入每一个点。若这个点与前面的有重复,要在所有与它重复的点lca离他距离最近处减去1的贡献。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1E6+5; 4 const int inf=INT_MAX; 5 int head[maxn*2],size,dfn[maxn],ti,back[maxn],fa[maxn][21],last[maxn],c[maxn],n,m,dep[maxn],ans[maxn],x,y,maxD; 6 struct edge{int to,next;}E[maxn*2]; 7 struct BIT 8 { 9 int t[maxn]; 10 int lowbit(int x){return x&-x;} 11 void add(int x,int y){while(x<=n){t[x]+=y;x+=lowbit(x);}} 12 int ask(int x){int ans=0;while(x){ans+=t[x];x-=lowbit(x);}return ans;} 13 }T; 14 struct query{int pos,d,num;}Q[maxn]; 15 vector<int>bel[maxn]; 16 set<int>pre[maxn]; 17 bool cmp(query x,query y){return dep[x.pos]+x.d<dep[y.pos]+y.d;} 18 void add(int u,int v) 19 { 20 E[++size].to=v; 21 E[size].next=head[u]; 22 head[u]=size; 23 } 24 void dfs(int u,int F,int d) 25 { 26 maxD=max(maxD,d); 27 fa[u][0]=F; 28 bel[d].push_back(u); 29 dfn[u]=++ti; 30 last[u]=back[ti]=u; 31 dep[u]=d; 32 for(int i=head[u];i;i=E[i].next) 33 { 34 int v=E[i].to; 35 if(v==F)continue; 36 dfs(v,u,d+1); 37 last[u]=last[v]; 38 } 39 } 40 void init() 41 { 42 for(int i=1;i<=20;++i) 43 for(int u=1;u<=n;++u)fa[u][i]=fa[fa[u][i-1]][i-1]; 44 } 45 int lca(int x,int y) 46 { 47 if(dep[x]<dep[y])swap(x,y); 48 int d=dep[x]-dep[y]; 49 for(int i=0;i<=20;++i) 50 if(d&(1<<i))x=fa[x][i]; 51 if(x==y)return x; 52 for(int i=20;i>=0;--i) 53 if(fa[x][i]!=fa[y][i]) 54 { 55 x=fa[x][i]; 56 y=fa[y][i]; 57 } 58 return fa[x][0]; 59 } 60 void insert(int x,int num) 61 { 62 T.add(num,1); 63 if(pre[x].size()==0) 64 { 65 pre[x].insert(num); 66 pre[x].insert(inf); 67 pre[x].insert(-1); 68 } 69 else 70 { 71 set<int>::iterator pr=pre[x].lower_bound(num); 72 set<int>::iterator pl=pr; 73 --pl; 74 num=back[num];//特别注意这里,此时的num已经是节点的编号而不是dfn序了 75 if(*pl==-1)T.add(dfn[lca(back[*pr],num)],-1); 76 else if(*pr==inf)T.add(dfn[lca(back[*pl],num)],-1); 77 else 78 { 79 int u=back[*pl],v=back[*pr]; 80 int l1=lca(u,num),l2=lca(v,num); 81 if(dep[l1]>dep[l2]) T.add(dfn[l1],-1); 82 else T.add(dfn[l2],-1); 83 } 84 pre[x].insert(dfn[num]); 85 } 86 } 87 int main() 88 { 89 ios::sync_with_stdio(false); 90 cin>>n>>m; 91 for(int i=1;i<=n;++i)cin>>c[i]; 92 for(int i=1;i<=n-1;++i) 93 { 94 cin>>x>>y; 95 add(x,y); 96 add(y,x); 97 } 98 dfs(1,1,1); 99 init(); 100 for(int i=1;i<=m;++i) 101 { 102 cin>>Q[i].pos>>Q[i].d; 103 Q[i].num=i; 104 } 105 sort(Q+1,Q+m+1,cmp); 106 int pos=1; 107 for(int i=1;i<=n;++i) 108 { 109 for(int j=0;j<bel[i].size();++j) 110 { 111 int u=bel[i][j]; 112 insert(c[u],dfn[u]); 113 } 114 while(pos<=m&&min(dep[Q[pos].pos]+Q[pos].d,maxD)==i) 115 { 116 ans[Q[pos].num]=T.ask(dfn[last[Q[pos].pos]])-T.ask(dfn[Q[pos].pos]-1); 117 ++pos; 118 } 119 } 120 for(int i=1;i<=m;++i)cout<<ans[i]<<endl; 121 return 0; 122 }

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1E5+5; 4 int n,m,head[maxn*2],size,x,y,fa[maxn],c[maxn]; 5 set<int>ans; 6 struct edge{int to,next;}E[maxn*2]; 7 void add(int u,int v) 8 { 9 E[++size].to=v; 10 E[size].next=head[u]; 11 head[u]=size; 12 } 13 void init(int u,int F) 14 { 15 fa[u]=F; 16 for(int i=head[u];i;i=E[i].next) 17 { 18 int v=E[i].to; 19 if(v==F)continue; 20 init(v,u); 21 } 22 } 23 void dfs(int u,int F,int d) 24 { 25 ans.insert(c[u]); 26 if(d==0)return; 27 for(int i=head[u];i;i=E[i].next) 28 { 29 int v=E[i].to; 30 if(v==F)continue; 31 dfs(v,u,d-1); 32 } 33 } 34 int main() 35 { 36 ios::sync_with_stdio(false); 37 cin>>n>>m; 38 for(int i=1;i<=n;++i)cin>>c[i]; 39 for(int i=1;i<=n-1;++i) 40 { 41 cin>>x>>y; 42 add(x,y); 43 add(y,x); 44 } 45 init(1,1); 46 while(m--) 47 { 48 cin>>x>>y; 49 ans.clear(); 50 dfs(x,fa[x],y); 51 cout<<ans.size()<<endl; 52 } 53 return 0; 54 }
(未填完)
Prob 4
树的问题太难了,我们先想链上问题怎么做。
链上问题还是太难了,我们先考虑只有质数怎么做。
只有质数的话,就转化为Prob3了。
再考虑链上一般的情况。我们只要把每个数质因式分解,对于固定的质数p以及它的次数k,看将它看做1~k种颜色的“和”。如:
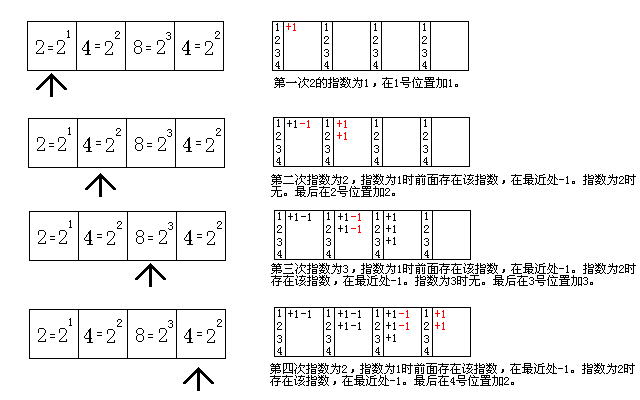
其余的类似。
这样继续沿用Prob3,可以推广到树上。开个set就行了。
代码看博主心情。
