[JLOI2016]圆的异或并

题意

https://www.luogu.org/problemnew/show/P3268

---

思考&别人的思考

包含关系有传递性和自反性，类似于小于号。

对于一条垂直与x轴的直线，有包含关系的圆的交点满足括号序列。如：

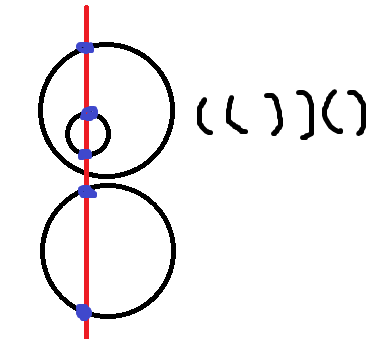
因此可以做扫描线。把圆分成上下两端弧，表示扫描线正与这些弧有交点，对于新添加的弧，判断第一个在其上方的弧是上半段还是下半段。若是上半段，则有包含关系；否则为并列关系。

只与小于号，由于我们维护的是与弧的焦点，又因为有交点时，其相对位置不会改变，因此只要维护交点的y坐标即可（只有查询和删除时用得到）。

---

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn=2E5+5;
ll n,f[maxn];
ll x,y,z,R[maxn],ans;
double now;
double s(double x)
{
    return x*x;
}
struct pt
{
    ll x,y,r,id;
    pt(ll X=0,ll Y=0,ll R=0,ll i=0)
    {
        x=X,y=Y,r=R,id=i;
    }
    bool operator<(pt A)const
    {
        if(x==A.x)
            return 0;
        return x<A.x;
    }
}a[maxn*2];
struct node
{
    pt A;
    ll flag;
    node(ll x=0,ll y=0,ll z=0,ll gg=0,ll g=0)
    {
        A=pt(x,y,z,gg),flag=g;
    }
    bool operator<(node x)const
    {
        double a=double(A.y)+flag*sqrt(s(double(A.r))-s(now-double(A.x))+0.000001);
        double b=double(x.A.y)+x.flag*sqrt(s(double(x.A.r))-s(now-double(x.A.x))+0.000001);
        return a<b;
    }
};
void out(multiset<node>S)
{
    multiset<node>::iterator pt=S.begin();
    while(pt!=S.end())
    {
        cout<<(*pt).A.r<<' '<<(*pt).A.x<<" "<<(*pt).A.y<<' '<<(*pt).A.id<<' '<<(*pt).A.y+(*pt).flag*sqrt(s((*pt).A.r)-s(now-(*pt).A.x)+0.001)<<" "<<now<<endl;
        ++pt;
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;++i)
    {
        cin>>x>>y>>z;
        a[2*i-1]=pt(x-z,y,z,i);
        a[2*i]=pt(x+z,y,z,i+n);
        f[i]=1;
        R[i]=z;
    }
    sort(a+1,a+2*n+1);
//    for(int i=1;i<=n*2;++i)
//        cout<<a[i].id<<' ';
//    cout<<endl;
    multiset<node>S;
    for(int i=1;i<=2*n;++i)
    {
        now=a[i].x;
        if(S.empty())
        {
//            cout<<a[i].x<<' '<<a[i].y<<' '<<a[i].r<<endl;
            S.insert(node(a[i].x+a[i].r,a[i].y,a[i].r,a[i].id,1));
            S.insert(node(a[i].x+a[i].r,a[i].y,a[i].r,a[i].id+n,-1));
        }
        else if(a[i].id<=n)
        {
//            cout<<a[i].x<<' '<<a[i].y<<' '<<a[i].r<<"---"<<endl;
            set<node>::iterator pt=S.upper_bound(node(a[i].x,a[i].y,a[i].r,1));
//            cout<<(*pt).A.id<<endl;
            if(pt==S.end())
            {
                --pt;
                f[a[i].id]=f[(*pt).A.id];
            }
            else if((*pt).A.id<=n)
                f[a[i].id]=-f[(*pt).A.id];
            else
                f[a[i].id]=f[(*pt).A.id-n];
            S.insert(node(a[i].x+a[i].r,a[i].y,a[i].r,a[i].id,1));
            S.insert(node(a[i].x+a[i].r,a[i].y,a[i].r,a[i].id+n,-1));
        }
        else
        {
//            cout<<"JJJ"<<a[i].x-a[i].r<<' '<<a[i].y<<" "<<a[i].r<<" "<<a[i].id<<endl;
            S.erase(node(a[i].x-a[i].r,a[i].y,a[i].r,a[i].id-n,1));
            S.erase(node(a[i].x-a[i].r,a[i].y,a[i].r,a[i].id,-1));
//            cout<<"CAO"<<S.size()<<endl;
        }
//        cout<<"NOW"<<"-----------"<<endl;
//        out(S);
//        cout<<endl;
    }
    for(int i=1;i<=n;++i)
    {
        ans+=s(R[i])*f[i];
//        cout<<f[i]<<' ';
    }
//    cout<<endl;
    cout<<ans<<endl;
    return 0;
}