第5章 对抗搜索

第五章 对抗搜索

一、博弈

定义

竞争环境中多个agent之间的目标是有冲突的，称为对抗搜索问题，也称为博弈（Games）。

特点

1. 有完整信息的、确定的、轮流行动的两个游戏者的零和游戏。（可为多人）
2. 难于求解
3. 注重时间效率

形式化

S0 初始状态
Player(s) 谁行动
Action(s) 状态s下的合法移动集合
Result(s,a) 转移模型
Terminal-test(s) 终止测试，游戏是否结束
Utility(s,p) 效用函数

博弈树

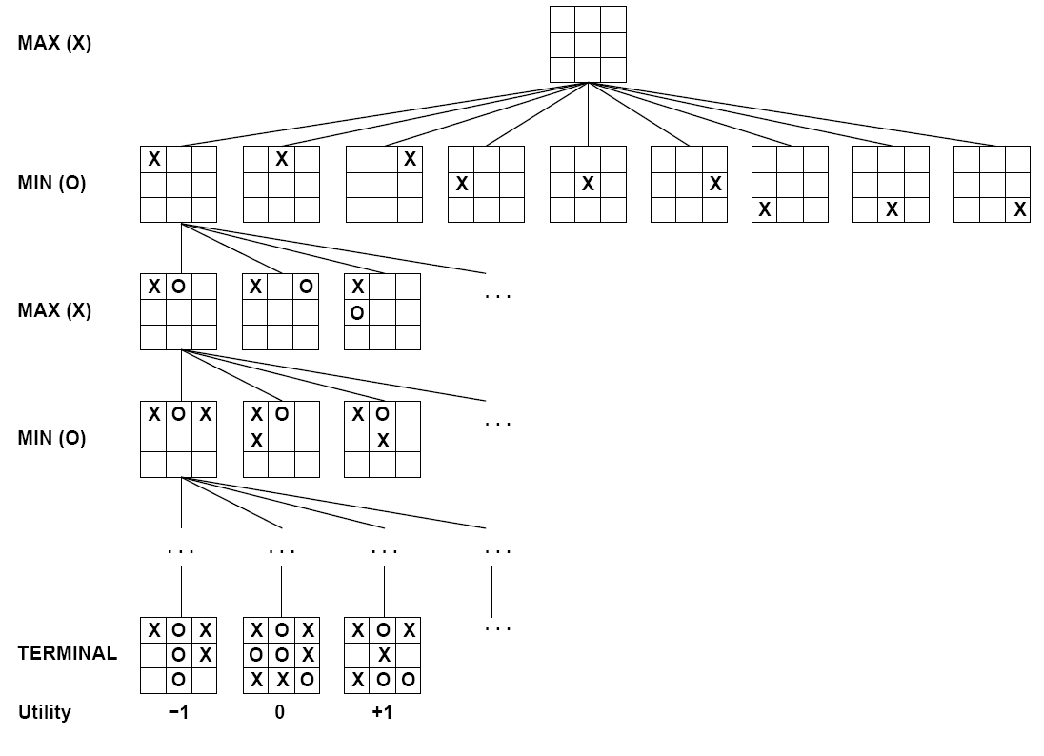
Tic-Tac-Toe游戏，结点为状态，边是移动。MAX与MIN轮流下棋，叶子结点上的数字是该终止状态下对MAX来说的效用值，值越高对MAX越有利，对MIN越不利。

二、博弈中的优化决策

极小极大算法

思想

采用递归算法自上而下一直前进到树的叶节点，然后随着递归通过搜索树把极小极大值回传。

在终止状态结点，结点返回效用值；

当轮到MAX时，结点返回子节点中效用值的极大值；

当轮到MIN时，结点返回子节点中效用值的极小值。

伪代码

action MINIMAX_DECISION(state){
    v=MAX_VALUE(state);
    return the action in SUCCESSORS(state) with value v;
}
value MAX_VALUE(state){
    if TERMINAL_TEST(state) then return UTILITY(state);
    v=-∞;
    foreach child of node
        v=MAX(v,MIN_VALUE(s));
    return v;
}
value MIN_VALUE(state){
    if TERMINAL_TEST(state) then return UTILITY(state);
    v=+∞;
    foreach child of node
        v=MIN(v,MAX_VALUE(s));
    return v;
}

性能

完备性

不一定完备，在状态空间有限且避免重复的情况下完备。

最优性

最优。

时间复杂度

[O(b^m) ]

空间复杂度

[一次性生成所有后继：O(bm) ]

[每次生成一个后继：O(m) ]

树的最大深度是m，每个结点合法的行棋有b个。

多人博弈

用向量来来取代单一值，这个向量代表从每个人角度出发得到的状态效用值。

可能出现联盟与破坏联盟的情况。

α-β剪枝

思想

剪掉那些不可能影响决策的分支。

α=到目前为止路径上发现的MAX的最佳选择；

β=到目前为止路径上发现的MIN的最佳选择；

搜索中不断更新α与β的值，当某结点的值比当前的α或β更差时剪裁此结点剩下的分支。

举例

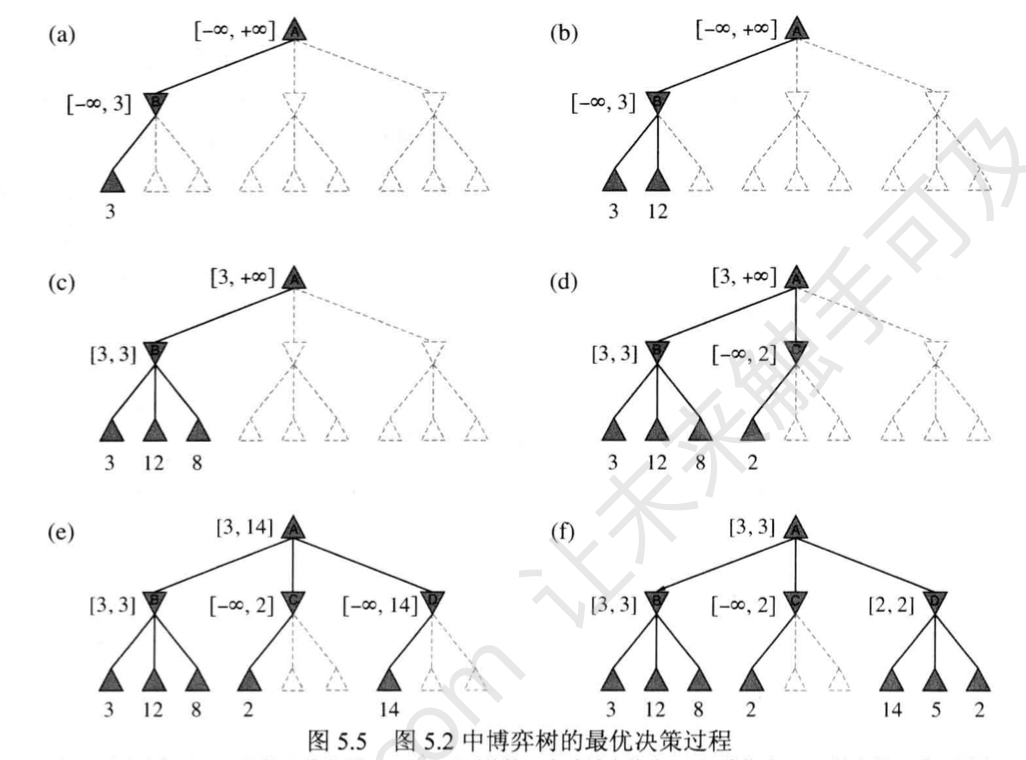
特点

α-β剪枝的效率很大程度上依赖于检查后继状态的顺序。

[最佳剪枝情况下可以将时间复杂度从极大极小算法的O(b^m)减少到O(b^{m/2} ); ]

[采用随机顺序检查的总结点数大约是O(b^{3m/4})。 ]

三、不完美的实时决策

资源限制

搜索空间巨大的问题，通过启发式评估函数EVAL(s)将非终止结点转变为终止结点与截断测试代替终止测试来解决。

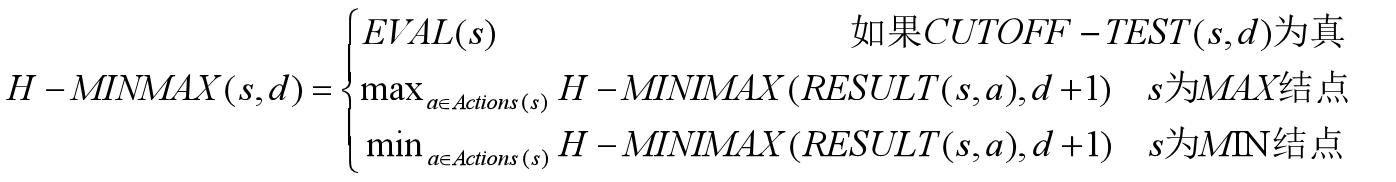
评估函数

定义准则

1. 对于终止状态的排序应该和效用函数一致
2. 计算时间不能太长
3. 对于非终止状态应该和取胜几率相关

评估值计算

期望

评估函数的效率值可能被映射到多个终止状态，用终止状态的概率来表示当前状态的期望值。

Eg.

假设根据经验，当出现两个兵对一个兵的状态，72% 获胜（效用+1）; 20% 输(效用0), 8% 平局(效用1/2)。
期望值为：0.721+0.20+0.08*(1/2)=0.76

线性加权评估

[Eval(s) = w_1f_1(s) + w_2f_2(s) + … + w_nf_n(s) ]

[w_i为权值，f_i为相应特征值 ]

Eg.

[对国际象棋来说，f_i可能是棋盘上每种棋子的数目，w_i可能是每种棋子的价值 ]

PS

线性评估假定特征之间是独立的，然而实际中特征之间具有关联性，比如国际象棋在残局中2个象比单个象的价值要高出2倍。

特征与权值来自于规律，这些规律可能要通过机器学习技术来确定评估函数的权值。

截断搜索

思想

在α-β剪枝算法中，将Terminal-test 被替换程cutoff-test(state,depth)，Utility被替换程eval(state)。

cutoff-test(state,depth)截断策略：

当大于固定深度时返回True；

根据游戏允许的时间来决定深度。

特点

评估函数的近似性会使截断搜索可能导致错误；

评估函数只适应于静态棋局，即不会很快出现大摇摆的棋局。

难以消除地平线效应（对方招数导致我方严重损失并且理论上基本无法避免），固定深度搜索会相信这些延缓招数能阻止实际无法避免的困境。

【单步延伸策略可以用来避免地平线效应，发现并记住一种“明显好于其他招数”的招数，当搜索达到指定深度界限，若单步延伸合法，则考虑此招。由于单步延伸很少，所以不会增加太多开销】

前向剪枝

思想

无需考虑直接剪枝一些子结点。

属于柱搜索的一种。柱搜索：每一层只考虑最好的n步棋

特点

可能导致最佳的行棋被剪掉

Product算法

思想

首先浅层搜索计算结点的倒退值v，再根据经验来估计深度d上的值是否在(α,β)范围外。

特点

使用先验的统计信息在一定程度上保护最佳行棋不被剪枝掉

搜索与查表

开局时的行棋大多依赖于人类的专业知识；

接近尾声的棋局可能性有限；

在开局和尾声阶段可以通过查表的方式来进行行棋。

四、随机博弈

思想

局面没有明确的极大极小值，只能计算棋局的期望值：机会结点所有可能结果的平均值。

将确定性博弈中的极小极大值一般化为包含机会结点的博弈的期望极大极小值。

举例

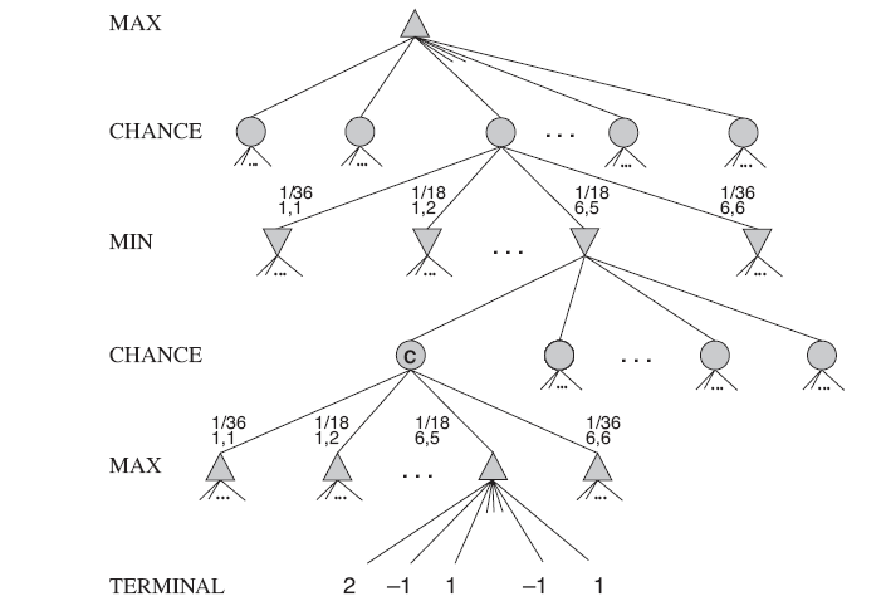
评估函数

评估函数应该与棋局获胜的概率成线性变换

时间复杂度

[O(b^mn^m) ]

五、部分可观察的博弈

军旗

棋子可以移动但对方看不见棋子是什么

使用信念状态

牌类

随机部分可观察

需要概率推算来制定决策

欢迎补充与指正，感谢点赞o(￣▽￣)ｄ