损失函数

1.损失函数

神经网络模型的效果及优化的目标是通过损失函数来定义的。回归和分类是监督学习中的两个大类。

（1）均方误差

 例子：

预测酸奶日销量y，x₁、x₂是影响日销量的因素。建模前，应预先采集的数据有：每日x₁、x₂和销量y_（即已知答案，最佳情况：产量=销量）

拟造数据集X,Y_： y_ = x₁ + x₂ 噪声：-0.05 ~ +0.05 拟合可以预测销量的函数

#! /usr/bin/env python
# -*- coding:utf-8 -*-
# __author__ = "yanjungan"


import tensorflow as tf
import numpy as np

SEED = 23455

rdm = np.random.RandomState(seed=SEED)  # 生成(0, 1)之间的随机数
# 生成32行2列（0, 1）
x = rdm.rand(32, 2)
# 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x]
# 强制转换x的数据类型
x = tf.cast(x, dtype=tf.float32)

w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))

epoch = 15000
lr = 0.002

for epoch in range(15000):
    with tf.GradientTape() as tape:
        y = tf.matmul(x, w1)
        loss_mse = tf.reduce_mean(tf.square(y_ - y))

    # 生成导数，梯度
    grads = tape.gradient(loss_mse, w1)

    # 更新w1, w1 = w1-lr*grads
    w1.assign_sub(lr*grads)

    if epoch % 500 == 0:
        print('After %d training steps, w1 is '% (epoch))
        print(w1.numpy(), "
")
print("Final w1 is:", w1.numpy())

 

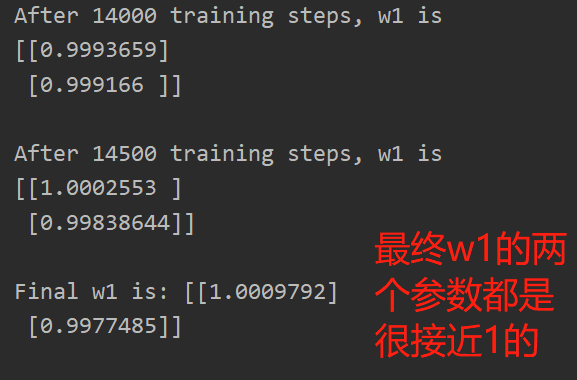
 最终w1的两个参数都是很接近1的，即，y=1.00*x₁+1.00*x₂，这一结果和我们制造数据集的公式y=1*x₁+1*x₂一致，说明预测酸奶的日销量拟合公式正确

 （2）交叉熵损失函数

 通过交叉熵的值，可以判断哪个预测的值（y）与实际值（y_）更接近，交叉熵越小，预测越准

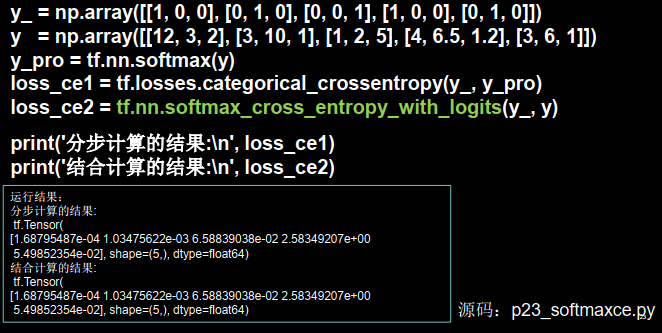
 2.softmax与交叉熵结合

我们在执行分类问题时，通常先用softmax函数让输出结果符合概率分布，再求交叉熵损失函数

tensorflow给出了可同时计算概率和交叉熵的函数

即输出先过softmax函数，再计算y与y_的交叉熵损失函数