1.磁盘原理
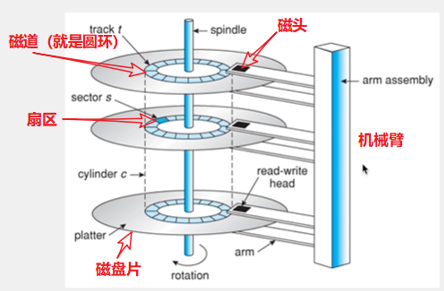
当磁盘需要读取某个地址数据的时候,首先会判断数据在哪个盘片上,确定好盘片之后呢,就开始选道,选道的过程就是通过伸展机械臂到数据对应的磁道(也就是圆环),再通过磁盘的旋转,找到对应的扇区,最后用磁头读取这几个扇区的数据到内存中去,因此可以看到读取磁盘数据是非常的耗时耗力的,尤其这里是机械操作。
因此如果用BST的方式在磁盘上存取数据,就会存在两个问题:
(1)由于二叉树只有两个分支,如果数据量非常大的话,树的高度就会很大,如果被查找的数据处于比较深的位置,那么磁盘寻址次数会非常的高,假设磁盘寻址+读取一次需要的时间是10ms,那么如果有一百万条数据,二叉树的高度会在20左右,这样一次查找,需要0.2s,一次性要查找100个数据,就需要20s,这个效率在数据库查找中是不可接受的
(2)磁盘读取过程中,是一次性读取8个扇区的,每个扇区的大小是512个字节,即一次性读取4k大小(blocksize)的数据,
我们看看数据库是如何设计的,一般情况下,一条数据是在几百个字节左右,如果每次都只读取一条信息,那势必会造成大量的空间浪费。
解决办法:(1)将树的高度降低,(2)尽量使得每次磁盘读取都能够得到最多的信息,
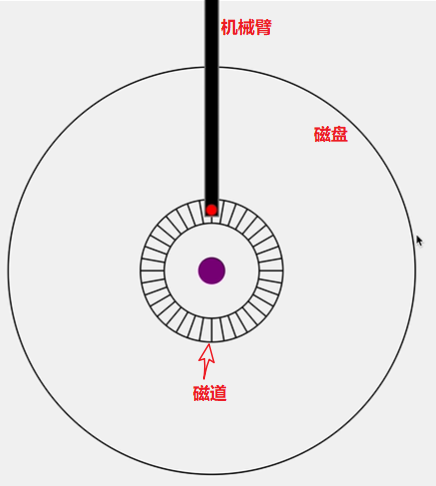
磁盘旋转,磁头读取数据到内存中

数据库中的信息
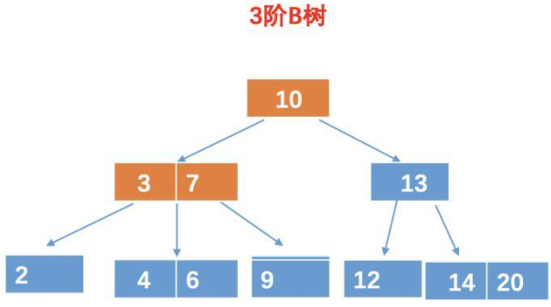
2.B树
B-Tree是为磁盘等外存储设备设计的一种平衡查找树。因此在讲B-Tree之前先了解下磁盘的相关知识。
系统从磁盘读取数据到内存时是以磁盘块(block)为基本单位的,位于同一个磁盘块中的数据会被一次性读取出来,而不是需要什么取什么。
InnoDB存储引擎中有页(Page)的概念,页是其磁盘管理的最小单位。InnoDB存储引擎中默认每个页的大小为16KB,可通过参数innodb_page_size将页的大小设置为4K、8K、16K。
而系统一个磁盘块的存储空间往往没有这么大,因此InnoDB每次申请磁盘空间时都会是若干地址连续磁盘块来达到页的大小16KB。InnoDB在把磁盘数据读入到磁盘时会以页为基本单位,在查询数据时如果一个页中的每条数据都能有助于定位数据记录的位置,这将会减少磁盘I/O次数,提高查询效率。
B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。
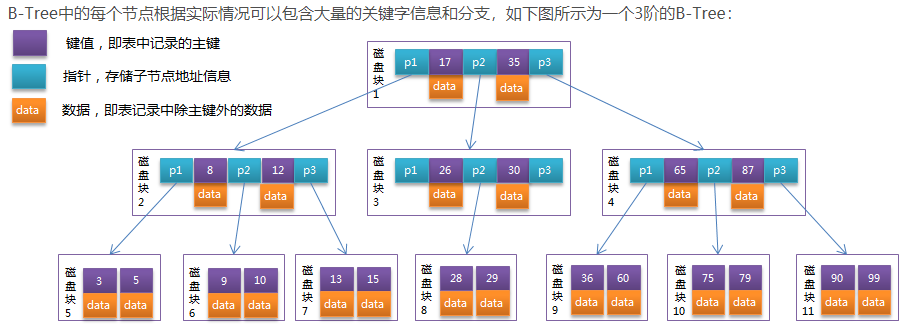
为了描述B-Tree,首先定义一条记录为一个二元组[key, data] ,key为记录的键值,对应表中的主键值,data为一行记录中除主键外的数据。对于不同的记录,key值互不相同。
通常,我们指定B树,需要指定其阶数(就是一个节点有多少个分叉),一棵m阶的B树,具有以下特性:
(1)每个节点最多m-1个关键字,也就是说,每个节点最多有m个分叉
(2)根节点最少可以有1个关键字,其他节点最少有 个关键字
个关键字
(3)和平衡二叉树类似,关键字的左侧数据都比关键字小,关键字的右侧数据都比关键字大
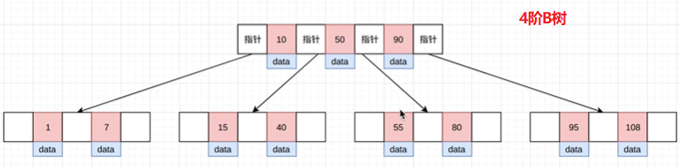
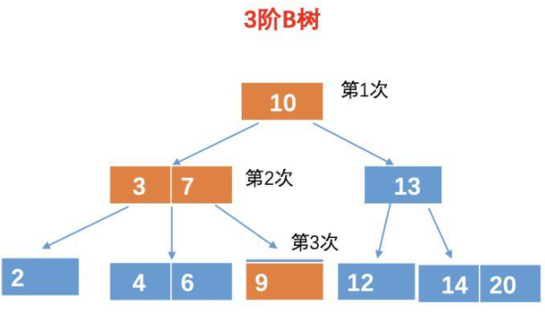
根节点有3个,4个分叉,10,50,90按从小到大排序
10的左侧的分叉是1和7,这是比10小的,10的右侧分叉是15和40,这是比10大的
可以看到,和二叉查找树还是很相似的,都是有序的,左孩子小,右孩子大,只是B树的一个节点可以有多个元素,且有多个分支。
3.B树的查询
为什么B树的查找效率会比二叉查找树高?
下面比较B树和二叉查找树的查找过程:
(1)在B树中的查询次数
假设,我们要查询元素9,对于B树,我们需要查询4次。
第一次比较:10 比较,比 10 小,所以再 10 的左孩子找。
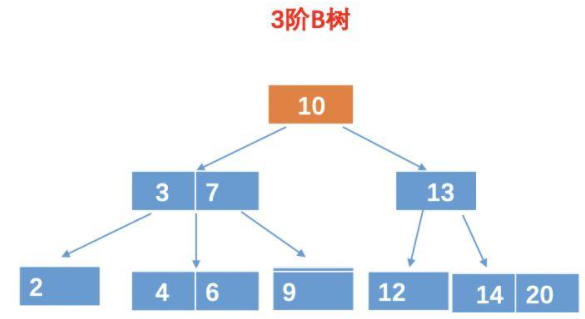
第二、三次比较:和 3 比较,比 3 大,这个时候我们还得和 7 比较。
第四次比较:和 9 比较,相等,找到目标树,返回。
所以最终的结果需要 4 次比较。
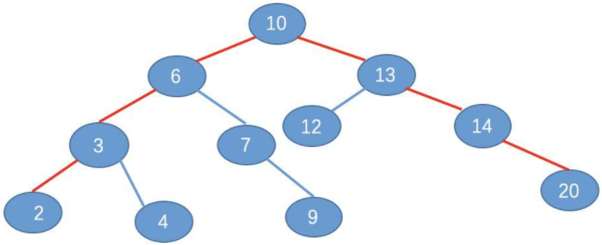
(2)在二叉树中的比较结果
也是需要4次比较
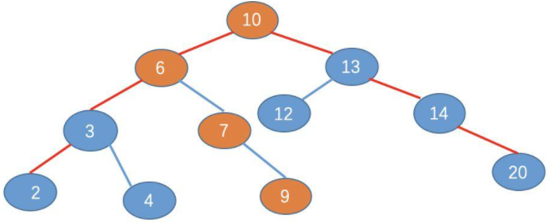
同样都是四次比较,而且,B 树的每一个节点,如果存放的元素比较多,那么 B 树的比较次数会更多,为什么就说 B 的效率比 二叉查找树快呢?
确实,如果单单从比较次数看的话,二叉查找树确实不比 B 树差,不过你忽略了一个很重要的点,那就是磁盘的寻址加载次数。
我们知道,在把磁盘里的数据加载到内存中的时候,是以页为单位来加载的,而我们也知道,节点与节点之间的数据是不连续的,所以不同的节点,很有可能分布在不同的磁盘页中。
所以对于上面的二叉查找树,我们可能需要进行 4 次寻址加载,如图:
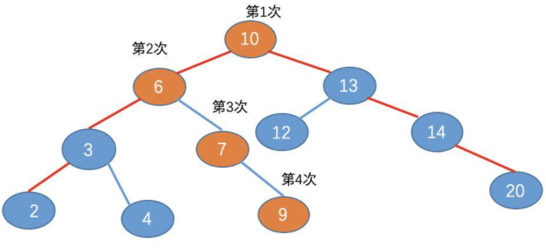
而对于 B 树,由于 B 树的每一个节点,可以存放多个元素,所以磁盘寻址加载的次数会比较少,例如上面的例子中,用 B 树的话,只需要加载 3 次,如图:
在内存的运算速度是非常快的,至少比磁盘的寻址加载速度,快了几百倍,而我们进行数值比较的时候,是在内存中进行的,虽然 B 树的比较次数可能比二叉查找树多,但是磁盘操作次数少,由之前阐述的读取磁盘是机械操作,耗时耗力。
所以总体来说,还是 B 树快的多,这也是为什么我们用使用 B 树来存储的原因。
根据B类树的特点,构造一个多阶的B类树,然后在尽量多的在结点上存储相关的信息,保证层数尽量的少,以便后面我们可以更快的找到信息,磁盘的I/O操作也少一些,而且B类树是平衡树,每个结点到叶子结点的高度都是相同,这也保证了每个查询是稳定的
实际上磁盘的加载次数,基本上是和树的高度相关联的,高度越高,加载次数越多,越矮,加载次数越少。所以对于这种文件索引的存储,我们一般会选择矮胖的树形结构。例如有 1000 个元素,如果是二叉查找树的话,高度可能高达 10 层,而如果用 10 阶 B 树的话,只需要三四层即可。
B 树除了会用在少部分的文件索引(数据库索引)外,应用的最多的就是文件系统了。
3.B+树
大部分文件索引或者数据库索引都是用 B+ 树的,而只有小部分才用 B 树。
由于B+树的数据都存储在叶子结点中,分支结点均为索引,方便扫库,只需要扫一遍叶子结点即可,但是B树因为其分支结点同样存储着数据,我们要找到具体的数据,需要进行一次中序遍历按序来扫,所以B+树更加适合在区间查询的情况,所以通常B+树用于数据库索引,而B树则常用于文件索引。
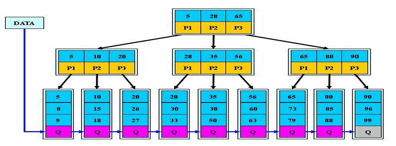
一个m阶树为例:
(1)根结点只有一个,分支数量范围为[2,m];
(2)分支结点,每个结点包含分支数范围为[ceil(m/2), m];
(3)分支结点的关键字数量等于其子分支的数量减一,关键字的数量范围为[ceil(m/2)-1, m-1],关键字顺序递增;
(4)所有叶子结点都在同一层;
注:ceil表示返回一个大于等于指定表达式的最小整数
其操作和B树的操作是类似的,不过需要注意的是,在增加值的时候,如果存在满员的情况,将选择结点中的值作为新的索引,还有在删除值的时候,索引中的关键字并不会删除,也不会存在父亲结点的关键字下沉的情况,因为那只是索引。
B树和B+树的区别:
这都是由于B+树和B具有这不同的存储结构所造成的区别,以一个m阶树为例。
(1)关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
(2)存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
(3)分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
(4)查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。
参考: