CSP2020第二轮J组简析
祝各位NOIPrp++
T1 优秀的拆分
**题,奇数-1,偶数从大往小枚举2的次方
#include<cstdio>
using namespace std;
int n,k;
long long a[30];
int main()
{
freopen("power.in","r",stdin);
freopen("power.out","w",stdout);
scanf("%d",&n);
if (n%2==1)
{
printf("-1
");
fclose(stdin);
fclose(stdout);
return 0;
}
a[0]=1;
k=0;
while (a[k]<=n)
a[k+1]=a[k]*2,++k;
for (int i=k;i;--i)
if (a[i]<=n) printf("%lld ",a[i]),n-=a[i];
fclose(stdin);
fclose(stdout);
return 0;
}
T2 直播获奖
如果成绩大点是个好题,但是这题成绩最大600,所以……直接上桶
然鹅我并没有切,原因
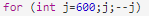
没到0呀!!!
#include<cstdio>
#include<iostream>
using namespace std;
int n,w,x,num,a[605];
int main()
{
freopen("live.in","r",stdin);
freopen("live.out","w",stdout);
scanf("%d%d",&n,&w);
for (int i=1;i<=n;++i)
{
scanf("%d",&x);
++a[x];
num=0;
for (int j=600;j>=0;--j)
{
num+=a[j];
if (num>=max(1,i*w/100))
{
printf("%d ",j);
break;
}
}
}
fclose(stdin);
fclose(stdout);
return 0;
}
T3 表达式
这次比赛最难的一题,比第四题难多了。原本CSP应该是T3dp,T4数据结构/图论,结果今年换了……
首先先根据读入的字符串建出一个二叉树
由于(1&x=x,0|x=x),所以这两种情况下(x)的取值可能会影响最后的结果。但是我们知道(0&x=0,1|x=1),所以在这两种情况下(x)的取值就无关紧要了,我们可以在二叉树里递归,然后打上无用标记
最后询问的时候看一下有没有标记,然后判断是否取反原来的结果
#include<cstdio>
#include<cstring>
#define N 1000005
using namespace std;
struct node
{
int res,fh,l,r;
}tree[N];
int n,m,len,x,tot,num,ans,a[N],q[N];
char s[N];
bool bj[N];
int number(int x)
{
int res=0;
while (s[x]>='0'&&s[x]<='9') res=(res<<1)+(res<<3)+(s[x]-'0'),++x;
return res;
}
void build(int now)
{
if (tree[now].fh==-1) bj[tree[now].l]=true;
else
{
if (tree[now].fh^tree[tree[now].l].res) build(tree[now].r);
if (tree[now].fh^tree[tree[now].r].res) build(tree[now].l);
}
}
int main()
{
freopen("expr.in","r",stdin);
freopen("expr.out","w",stdout);
gets(s);
len=strlen(s);
scanf("%d",&n);
for (int i=1;i<=n;++i)
scanf("%d",&a[i]);
for (int i=0;i<len;++i)
{
if (s[i]=='x')
{
x=number(i+1);
tree[++tot].res=a[x];
tree[tot].l=tree[tot].r=x;
tree[tot].fh=-1;
q[++num]=tot;
}
if (s[i]=='&')
{
tree[++tot].fh=0;
tree[tot].l=q[num];
tree[tot].r=q[--num];
tree[tot].res=(tree[tree[tot].l].res)&(tree[tree[tot].r].res);
q[num]=tot;
}
if (s[i]=='|')
{
tree[++tot].fh=1;
tree[tot].l=q[num];
tree[tot].r=q[--num];
tree[tot].res=(tree[tree[tot].l].res)|(tree[tree[tot].r].res);
q[num]=tot;
}
if (s[i]=='!') tree[q[num]].res=!(tree[q[num]].res);
}
ans=tree[tot].res;
build(tot);
scanf("%d",&m);
for (int i=1;i<=m;++i)
{
scanf("%d",&x);
if (bj[x]) printf("%d
",!ans);
else printf("%d
",ans);
}
fclose(stdin);
fclose(stdout);
return 0;
}
T4 方格取数
(dp),由于不能往左走,所以按列dp。每个点从3个方向转移,注意要么一直到上,要么一直到下,因为不能重复
#include<cstdio>
#include<iostream>
#define ll long long
#define inf 2147483600
using namespace std;
int n,m,a[1005][1005];
ll f[1005][1005][5];
int main()
{
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;++i)
for (int j=1;j<=m;++j)
scanf("%d",&a[i][j]);
for (int i=0;i<=n;++i)
for (int j=0;j<=m;++j)
f[i][j][1]=f[i][j][2]=f[i][j][3]=-inf;
f[1][1][1]=f[1][1][2]=f[1][1][3]=a[1][1];
for (int j=1;j<=m;++j)
{
for (int i=1;i<n;++i)
f[i+1][j][1]=max(f[i][j][1],f[i][j][3])+a[i+1][j];
for (int i=n;i>1;--i)
f[i-1][j][2]=max(f[i][j][2],f[i][j][3])+a[i-1][j];
for (int i=1;i<=n;++i)
f[i][j+1][3]=max(f[i][j][1],max(f[i][j][2],f[i][j][3]))+a[i][j+1];
}
printf("%lld
",max(f[n][m][1],max(f[n][m][2],f[n][m][3])));
fclose(stdin);
fclose(stdout);
return 0;
}
好像有点短……简析嘛