1.简介
算法思想:基于分治的思想,是冒泡排序的改进型。首先在数组中选择一个基准点(该基准点的选取可能影响快速排序的效率,后面讲解选取的方法),然后分别从数组的两端扫描数组,设两个指示标志(lo指向起始位置,hi指向末尾),首先从后半部分开始,如果发现有元素比该基准点的值小,就交换lo和hi位置的值,然后从前半部分开始扫秒,发现有元素大于基准点的值,就交换lo和hi位置的值,如此往复循环,直到lo>=hi,然后把基准点的值放到hi这个位置。一次排序就完成了。以后采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时该数组就自然有序了。
排序过程:
排序过程:

下面贴上一张动图:
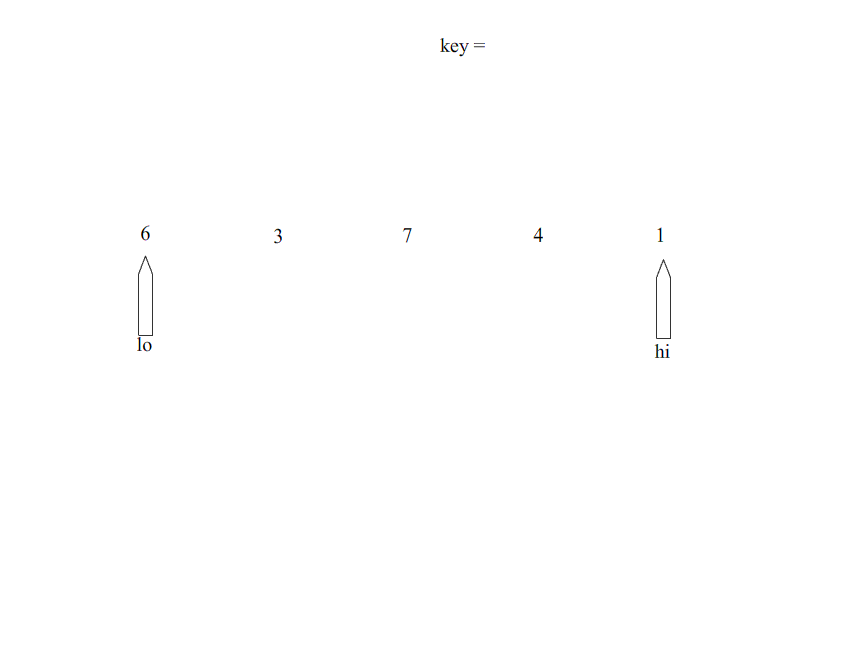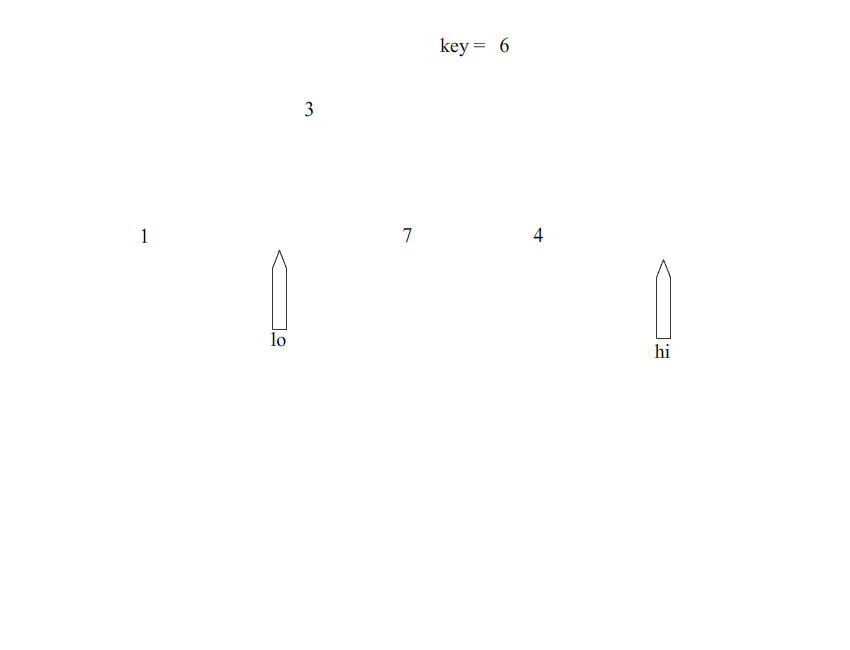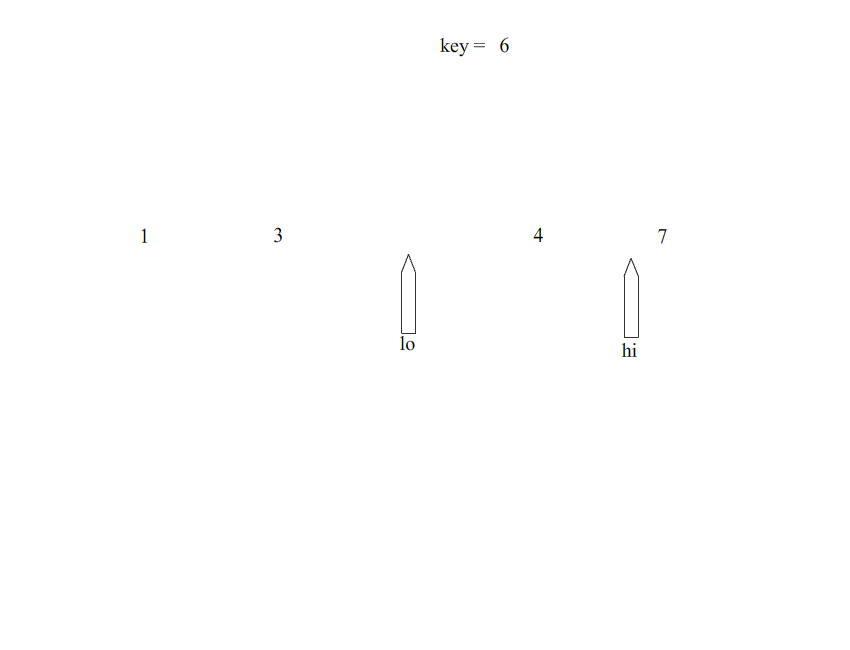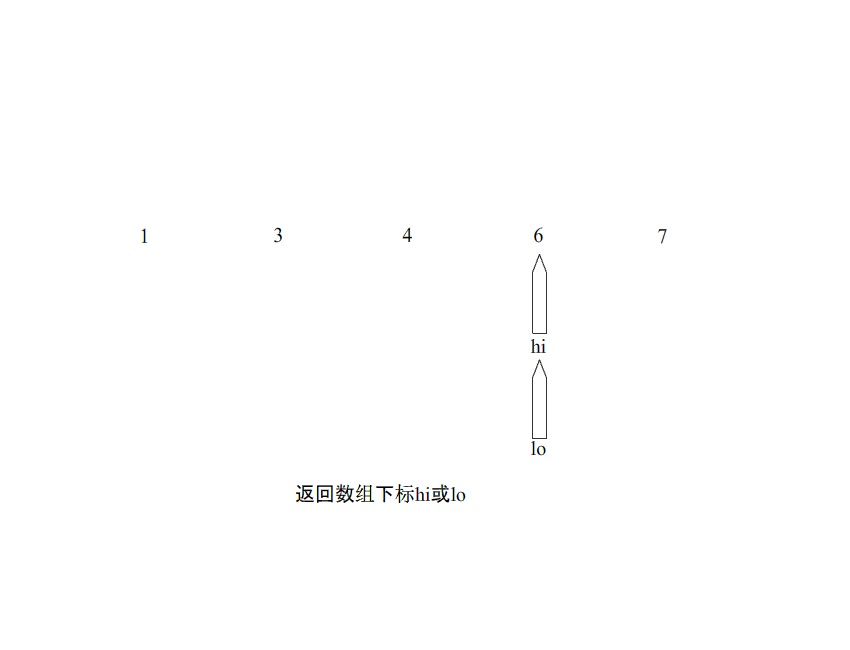
给出C代码实现:
#include <stdio.h> int partition(int* arr,int lo,int hi); void quickSort(int* arr,int lo,int hi); int main() { int arr[]={1,8,2,9,3,7,0,1,0,10}; quickSort(&arr,0,9); for(int i=0;i<10;i++){ printf("%d ",arr[i]); } return 0; } int partition(int* arr,int lo,int hi){ int key=arr[lo]; //固定切分,选择最左边的点,作为基准点 while(lo<hi){ while(lo<hi && arr[hi]>=key){ //从右边进行遍历 hi--; } arr[lo]=arr[hi]; while(lo<hi && arr[lo]<=key){ //从左边进行遍历 lo++; } arr[hi]=arr[lo]; } arr[lo]=key; return lo; } void quickSort(int* arr,int lo,int hi){ if(lo>=hi){ return; } int index=partition(arr,lo,hi); //得出分界点 quickSort(arr,lo,index-1); quickSort(arr,index+1,hi); }
2.快速排序优化
对于基准位置的选取一般有三种方法:固定切分,随机切分和三数取中切分。三数取中选择基准点,是最理想的一种。
三数取中切分:
int partition(int* arr,int lo,int hi){ //三数取中,使中间数处于lo下标处 int mid=lo+(hi-lo)/2; if(arr[mid]>arr[hi]){ swapArray(arr,mid,hi); } if(arr[lo]>arr[hi]){ swapArray(arr,lo,hi); } if(arr[mid]>arr[lo]){ swapArray(arr,mid,lo); } //调换后的结果,arr[hi]最大,arr[lo]其次,arr[mid]最小 int key=arr[lo]; while(lo<hi){ while(lo<hi && arr[hi]>=key){ hi--; } arr[lo]=arr[hi]; while(lo<hi && arr[lo]<=key){ lo++; } arr[hi]=arr[lo]; } arr[hi]=key; return hi; } //互换数组中两个下标元素的值 void swapArray(int* arr,int a,int b){ int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; }
3.快排的时间复杂度
在讨论了快排的基本实现之后,接下里继续讨论快排的时间复杂度。快排的平均时间复杂度O(NlogN),最差时间复杂度O(N^2)。