Lca求法 （树链剖分 与 倍增）

LCA是啥

不会吧不会吧不会真的有人要看LCA是啥吧
LCA就是最小公共祖先
即给出一棵树 大概是这样

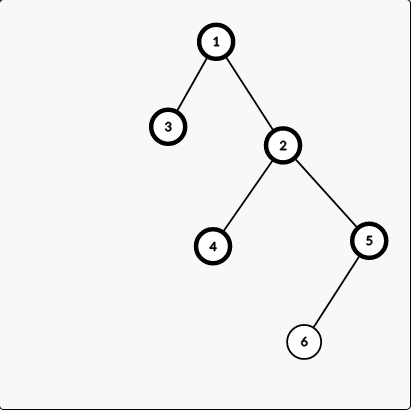
4 和 5 的最小公共祖先便是2
2 和 3 的最小公共祖先是1
1 和 2 的最小公共祖先是1

倍增求LCA

首先来考虑一种朴素算法

• 我们已知两个树上的点u,v 想要求u，v的最小公共祖先
• 然后我们可以将u，v中深度较深的一个点跳到与v深度相同，然后u，v一起向上跳，直到u和v变成同一个点
• 思路很好理解，看代码实现

//没有代码实现 这么简单你还要看代码？？
//其实有…………
//假定我们已经预处理好了dep深度和fa父亲
int lca(int u,int v){
	if(dep[v] < dep[u])swap(u,v);
	while(dep[u] != dep[v])v = fa[v];
	while(u != v){
		u = fa[u];
		v = fa[v];
	}
	return fa[u];
}

• 那倍增怎么实现呢？
• 其实就是在预处理某个节点的祖先的同学 把它的(2^k)级祖先也处理出来 类似与递推fa[u][i] = fa[fa[u][i-1]][i-1]，显然u的(2^i)级祖先就是u的(2^i-1)级祖先的(2^i-1)级祖先 （(2^i-1) + (2^i-1) = (2^i)）
• 然后就是最后向上跳 显然我们要从大距离向小距离跳 因为如果我们跳1,2，4,8，16这样的步数 那么到后面如果相差13个到达LCA 是无法抵达的（或者较难处理）
• 而我们如果16，8,4，2,1这样跳就不会出现类似的情况
• 判断的时候我们也不能判断u与v是否相等了 而应该是fa[u][0]与fa[v][0] 如果我们判断u != v时向上跳 最后停留的位置不一定是正解位置
  但是如果判断fa[u][0] != fa[v][0] 就不一样了

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5+10;
int cnt,head[maxn];
int dep[maxn << 1],fa[maxn][30];

struct node{
	int next,to;
}a[maxn << 1];

void add(int x,int y){
	a[++cnt].to = y;
	a[cnt].next = head[x];
	head[x] = cnt;
}

void dfs(int u){
	dep[u] = dep[fa[u][0]] + 1;
	for(int i = 1;(1 << i) <= dep[u];++i){
		fa[u][i] = fa[fa[u][i-1]][i-1];
	}
	for(int i = head[u];i;i = a[i].next){
		int v = a[i].to;
		if(v == fa[u][0])continue;
		fa[v][0] = u;
		dfs(v);
	}
}

int lca(int u,int v){
	if(dep[u] < dep[v])swap(u,v);
	int len = dep[u] - dep[v],k = 0;
	while(len){
		if(len & 1)u = fa[u][k];
		++k;
		len >>= 1;
	}
	if(u == v)return u;
	for(int i = 20;i >= 0;--i){
		if(fa[u][i] != fa[v][i]){
			u = fa[u][i];
			v = fa[v][i];
		}
	}
	return fa[u][0];
}

int main(){
	int n,m,s;scanf("%d%d%d",&n,&m,&s);
	for(int i = 1;i < n;++i){
		int x,y;scanf("%d%d",&x,&y);
		add(x,y);add(y,x);
	}
	dfs(s);
	for(int i = 1;i <= m;++i){
		int u,v;scanf("%d%d",&u,&v);
		printf("%d
",lca(u,v));
	}
	return 0;
}

树链剖分求LCA

前置知识

• 重儿子：子树结点数目最多（size最大）的结点
• 轻儿子：除重儿子之外的所有儿子
• 重边：父亲结点和重儿子连成的边；
• 轻边：父亲节点和轻儿子连成的边；
• 重链：由多条重边连接而成的路径；
• 轻链：由多条轻边连接而成的路径

算法

• 树链剖分处理重儿子和轻儿子以及链顶的操作并不很难
• 所以实际上树链剖分求LCA 比倍增还要简单
• 如果不理解树链剖分的可以去自行查找题解
• 显然我们通过树链剖分的处理可以分出重儿子和轻儿子，而且可以处理好链顶节点
• 如果u，v两个点不属于同一条链，就让深度较深那个点跳到链顶，然后再次比较，知道两个点在同一条链上
• 在同一条链上后就可以直接返回深度较小那个节点了

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5+10;

int cnt,head[maxn];
int fa[maxn],dep[maxn],son[maxn];
int size[maxn],top[maxn];

struct node{
	int next,to;
}a[maxn << 1];

void add(int x,int y){
	a[++cnt].to = y;
	a[cnt].next = head[x];
	head[x] = cnt;
}

void dfs(int u){
	size[u] = 1;
	dep[u] = dep[fa[u]] + 1;
	for(int i = head[u];i;i = a[i].next){
		int v = a[i].to;
		if(v == fa[u])continue;
		fa[v] = u;
		dfs(v);
		size[u] += size[v];
		if(!son[u] || size[son[u]] < size[v])son[u] = v;
	}
}

void Dfs(int u,int tp){
	top[u] = tp;
	if(son[u])Dfs(son[u],tp);
	for(int i = head[u];i;i = a[i].next){
		int v = a[i].to;
		if(v != fa[u] && v != son[u])Dfs(v,v);
	}
}

int lca(int u,int v){
	while(top[u] != top[v]){
		if(dep[top[u]] >= dep[top[v]])u = fa[top[u]];
		else v = fa[top[v]];
	}
	return dep[u] < dep[v] ? u : v;
}

int main(){
	int n,m,s;scanf("%d%d%d",&n,&m,&s);
	for(int i = 1;i < n;++i){
		int x,y;scanf("%d%d",&x,&y);
		add(x,y);add(y,x);
	}
	dfs(s);
	Dfs(s,s);
	for(int i = 1;i <= m;++i){
		int u,v;scanf("%d%d",&u,&v);
		printf("%d
",lca(u,v));
	}
	return 0;
}