题目描述
无向连通图G 有n 个点,n - 1 条边。点从1 到n 依次编号,编号为 i 的点的权值为W i ,每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ,若它们的距离为2 ,则它们之间会产生Wu×Wv 的联合权值。
请问图G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入输出格式
输入格式:输入文件名为link .in。
第一行包含1 个整数n 。
接下来n - 1 行,每行包含 2 个用空格隔开的正整数u 、v ,表示编号为 u 和编号为v 的点之间有边相连。
最后1 行,包含 n 个正整数,每两个正整数之间用一个空格隔开,其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。
输出格式:输出文件名为link .out 。
输出共1 行,包含2 个整数,之间用一个空格隔开,依次为图G 上联合权值的最大值
和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对10007 取余。
输入输出样例
输入样例#1:
5 1 2 2 3 3 4 4 5 1 5 2 3 10
输出样例#1:
20 74
说明
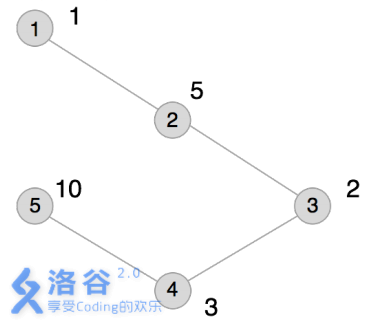
本例输入的图如上所示,距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。
其联合权值分别为2 、15、2 、20、15、20。其中最大的是20,总和为74。
【数据说明】
对于30% 的数据,1 < n≤ 100 ;
对于60% 的数据,1 < n≤ 2000;
对于100%的数据,1 < n≤ 200 , 000 ,0 < wi≤ 10, 000 。
题解:
bfs,以每个点为中心,它儿子的距离都为2
求最大值只需找前两大的w,求和可以用sum=(a1+a2+a3+......+an)^2-a1^2-a2^2-......-an^2
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #define RG register 9 #define ll long long 10 using namespace std; 11 12 const int maxn = 200010; 13 const int maxm = 200010; 14 const int mod = 10007; 15 16 17 int n,ans1,ans2; 18 int nxt[maxm*2],to[maxm*2],h[maxn],e_num,w[maxn]; 19 bool vis[maxn]; 20 21 queue<int> q; 22 23 void add(int x, int y) {nxt[++e_num]=h[x],to[e_num]=y,h[x]=e_num;} 24 25 void bfs() { 26 q.push(1),vis[1]=1; 27 while(!q.empty()) { 28 ll sum=0; int mx1=0,mx2=0; 29 int u=q.front(); q.pop(); 30 for(int i=h[u]; i; i=nxt[i]) { 31 int v=to[i]; 32 if(w[v]>mx1) mx2=mx1,mx1=w[v]; 33 else if(w[v]>mx2) mx2=w[v]; 34 sum+=(ll)w[v]; 35 if(!vis[v]) vis[v]=1,q.push(v); 36 } 37 sum=sum*sum; 38 for(int i=h[u]; i; i=nxt[i]) { 39 int v=to[i]; 40 sum-=(ll)w[v]*w[v]; 41 } 42 sum%=mod; 43 ans1=max(ans1,mx1*mx2),ans2+=sum,ans2%=mod; 44 } 45 } 46 47 int main() { 48 scanf("%d", &n); 49 for(int i=1; i<n; i++) { 50 int x,y; 51 scanf("%d%d", &x, &y); 52 add(x,y),add(y,x); 53 } 54 for(int i=1; i<=n; i++) scanf("%d", &w[i]); 55 bfs(); 56 ans2%=mod; 57 printf("%d %d", ans1, ans2); 58 return 0; 59 }