千年难得一见,我居然没翻车???
awa
成功进入了rank3,然鹅。。。
前8名全是前3。。。
妙不可言awa
只要拿到了基础分的200,就是前3awa
哦对了,T4是原本的T1。。
T1是原本的T2,T2是原本的T3,T3是原本的T4
老师昨天题目加错了。。。
所以就一大群人A了T4 awa
快乐
T1
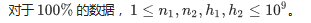
给出n1,n2,h1,h2
简单题,但是要long,long
直接给结论,随便推一推就好了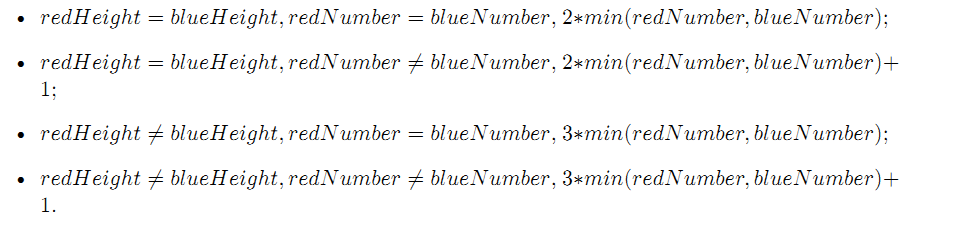
#include <bits/stdc++.h> #define ll long long using namespace std ; ll a,b,x,y,ans; inline ll read() { register ll Q=0,f=1;register char C=getchar() ; while(C<'0'or C>'9')f=C=='-'?-1:1,C=getchar() ; while(C<='9'and C>='0')Q=(Q<<1)+(Q<<3)+C-'0',C=getchar() ; return f*Q; } int main() { freopen("tower.in","r",stdin); freopen("tower.out","w",stdout); a=read();x=read(); b=read();y=read(); if(a>b) { swap(a,b); } if(x==y) { ans+=a*2; } else { ans+=a*3; } if(a!=b)ans++; cout<<ans<<endl; return 0; }
T2
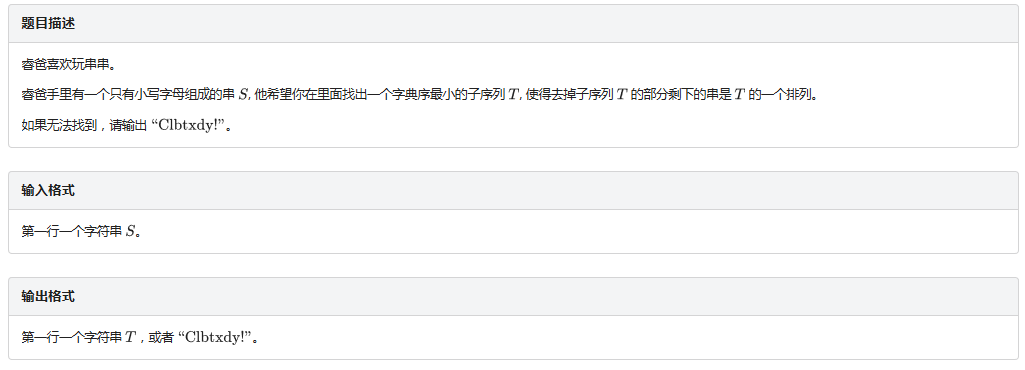
题目的意思非常的补坑描述,我看了5分钟才看懂。。。
就是要你在一个字符串里面在找出一个子序列(不用连续,但是要求顺序不能倒)
取出以后,原本的序列要求变成取出的序列的一个排列,就是有且仅有取出的序列的全部字符
原本吧,如果真的是只有我说的这些要求,那就是一道简单题.
如果把题目里面的字典序最小去掉,我分分钟就能A了它,可惜去不得
显然,子序列T的合法要求就是,在原序列S中,每个字符出现的次数必须是T中出现的次数的两倍,否则一定不合法。
所以要如果不要保证字典序最小,这题就讲完了。。。
淦
awa
其实后面也不难搞,只用按位贪心一下,每一位都要贪心的选出能够保证后面合法的,且字典序最小的方案。
因为字典序本身就是一种贪心。。。
如果是判断一个字母是否合法,只需要判断前面字母使用的次数和用完以后还有几个剩余,就是正解了
awa
#include <bits/stdc++.h> #define ll long long using namespace std ; inline ll read() { register int Q=0,f=1;register char C=getchar() ; while(C<'0'or C>'9')f=C=='-'?-1:1,C=getchar() ; while(C<='9'and C>='0')Q=(Q<<1)+(Q<<3)+C-'0',C=getchar() ; return f*Q; } int s[27],ss[27],ans[27][210],m=0,n; char ch[210]; void cherk() { for(int i=0;i<26;ss[i]=s[i],i++) { if(s[i]%2!=0) { puts("Clbtxdy!"); exit(0); } } } void work() { for(int i=1;i<=n;i++) { int mx=0; for(int j=i;j<=n;j++) { int x=ch[j]-'a'; bool ff=0; for(int k=0;k<26;k++) { if(x==k) { if(ans[k][j]>s[k]/2+1) { ff=1; break; } } else { if(ans[k][j]>s[k]/2) { ff=1; break; } } } if(!ff && ss[ch[j]-'a']>0) { if(mx==0) { mx=j; } else { if(ch[j]-'a'<ch[mx]-'a') { mx=j; } } } } if(mx==0) mx=i; cout<<ch[mx]; ss[ch[mx]-'a']-=2; s[ch[mx]-'a']+=2; m++; if(m==n/2) { exit(0); } i=mx; } } int main() { freopen("string.in","r",stdin); freopen("string.out","w",stdout); scanf("%s",ch+1); n=strlen(ch+1); for(int i=1;i<=n;i++) { s[ch[i]-'a']++; for(int j=0;j<26;j++) { if(ch[i]-'a'!=j) { ans[j][i]=ans[j][i-1]; } else { ans[j][i]=ans[j][i-1]+1; } } } cherk(); work(); return 0; }
T3
是个博弈论
这个问题,有一个很麻烦的地方,就是如果是个dp的话,它的状态会十分的复杂,因为我要同时去考虑两种状态:1.睿爸的。2.杜教的。
但是考虑到我们最后的答案,其实要求的就是杜教扣了睿爸多少,所以就可以把睿爸取到的数先全部都加上(包括杜教的),然后再减去全部的数(只有杜教的),这就是答案。
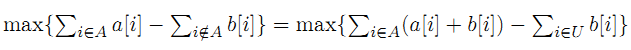
其中的A是睿爸能取到的数。
U是全集
所以我们要做的事情其实就是最大化a[i]+b[i]。
那就很好搞啦!
但是这个并没有到达博弈论的部分。
其实根本就是个贪心。。。
这只是为了方便去计算我们的答案罢了
现在问题已经被简化了,我们来讨论一下博弈(贪心)的策略。
因为答案和栈中的元素有关,而栈也是只有两个元素,所以这不就是在叫着:“讨论我!讨论我!”吗。。。
对于一个栈的价值,其实就是如我们上面说的,a[i]+b[i]。这个就是为什么先推出来上面的式子。
这个让我们讨论价值这件事情变得可能。
结论1:如果一个栈的价值a+b<=c+d,先手永远只能拿到上面的,而后手总能拿到下面的。
证明1:如果先手拿了一个栈顶,那么后手一定是可以直接拿栈底的
那如果他没拿呢?
那先手就是憨。
因为没拿,就说明了另一个栈顶的元素肯定是要比这个栈底大的。根据我们的前提条件,先手拿的栈顶的元素是比栈顶小的。
拿为什么先手不拿这个栈顶呢?它不香吗?
证毕。
awa
于是我们就快乐的排除掉了a+b<=c+d的栈。因为他们的贡献是十分显然的。
接下来考虑一下a+b>c+d的栈。
结论2:对于a+b>c+d的栈,肯定是先后手交替拿取目前最大的元素
证明2:
因为前面证明了最优的策略就是使拿到的元素两个值相加起来最大。
所以我们肯定是要先拿取最大是元素的。
因为全部的栈都已经是a+b>c+d了,所以不会存在冲突的情况。
这样就好了啊awa
ac!awa
#include <bits/stdc++.h> #define ll long long using namespace std ; ll a[200001],b[200001],c[200001],d[200001],n;bool vis[200001]; ll ans1,ans2; inline ll read() { register ll Q=0,f=1;register char C=getchar() ; while(C<'0'or C>'9')f=C=='-'?-1:1,C=getchar() ; while(C<='9'and C>='0')Q=(Q<<1)+(Q<<3)+C-'0',C=getchar() ; return f*Q; } int main() { freopen("dortmund.in","r",stdin); freopen("dortmund.out","w",stdout); n=read(); for(ll i=1;i<=n;i++) { a[i]=read();b[i]=read(); c[i]=read();d[i]=read(); } for(ll i=1;i<=n;i++) { if(a[i]+b[i]<=c[i]+d[i]) { ans1+=a[i]+b[i]; } } priority_queue<pair<ll,ll> > q; for(ll i=1;i<=n;i++) { if(a[i]+b[i]>c[i]+d[i]) { q.push(make_pair((a[i]+b[i]),i)); } } ll awsd=1; while(q.size()!=0) { // cout<<1<<endl; pair<ll,ll> x=q.top(); ll now=x.first; if(awsd==1) { ans1+=now; awsd=2; } else { awsd=1; } if(vis[x.second]==false) { q.push(make_pair((c[x.second]+d[x.second]),x.second)); vis[x.second]=true; } q.pop(); } for(ll i=1;i<=n;i++) { ans1-=b[i]; ans1-=d[i]; } cout<<ans1<<endl; return 0; }
呼~总算是写完了awa
T4

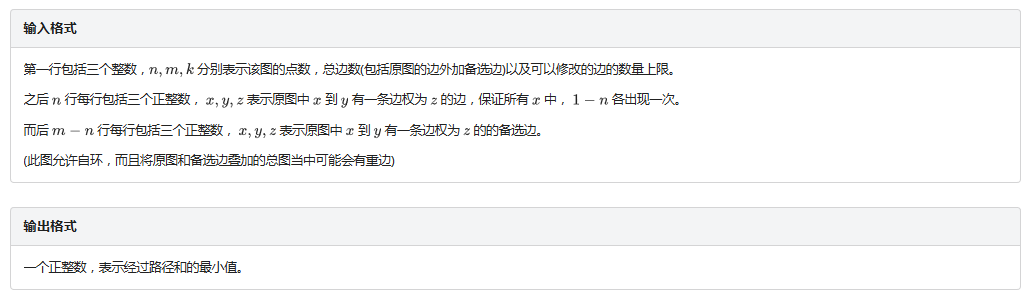
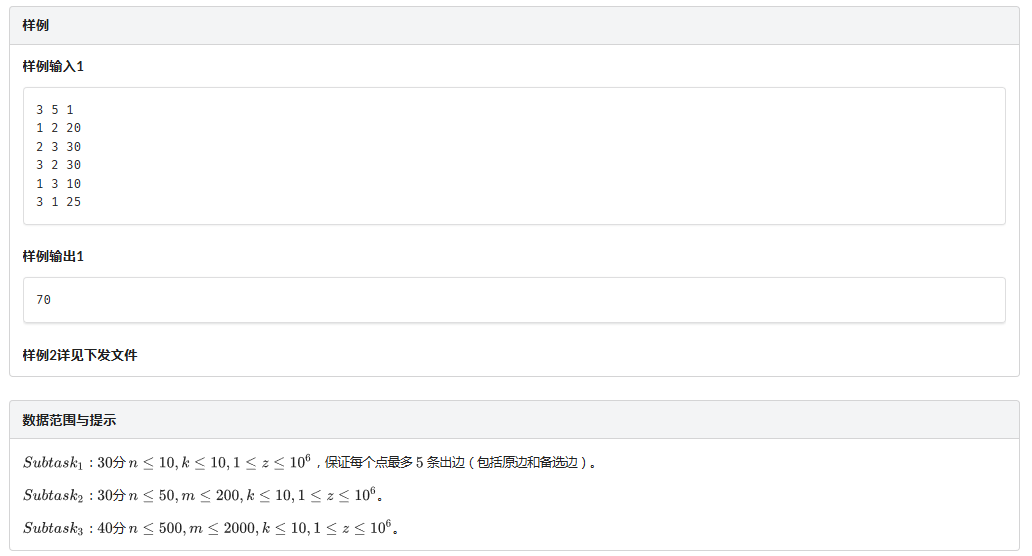
一看就是图论题(逃
一看就是最短路awa
这个嘛。。。
不就是最短路和dp的结合题吗。。。
很典型啊。。。
最短路嘛,是有状态的,所以像这总多了一个限制条件的问题,我想应该是能够用加一维状态的办法来解决的。
啥不行就给啥加状态awa(逃
其实总是加状态也是不行的,因为时空间复杂度撑不住啊awa
还是要看情况的awa
这个题解我是真的看不懂。。。

直接放上来吧。。。
说的我好迷啊awa
淦,原来是我没写过几道分层图的dp。。。
我说为什么我最短路配dp总是不会写。。。
淦
不写了,补坑去了awa
代码用了机房dalao lsf的神奇dfs,跑的比正解还快,而且好写。。。
本质就是一个朴素的dfs。。。。
code
#include <bits/stdc++.h> #define ll long long using namespace std; struct edge { ll to,next,v;bool f; }e[10001]; ll head[10001],tot,n,m,k;bool vis[10001],vis2[10001];int dis[1001][20],ans=INT_MAX; inline ll read() { register ll Q=0,f=1;register char C=getchar() ; while(C<'0'or C>'9')f=C=='-'?-1:1,C=getchar() ; while(C<='9'and C>='0')Q=(Q<<1)+(Q<<3)+C-'0',C=getchar() ; return f*Q; } void add(int i,int j,int v,bool flag) { e[++tot].next=head[i]; e[tot].to=j; head[i]=tot; e[tot].v=v; e[tot].f=flag; } void dfs(int x,int sum,int cnt) { if(cnt>k) { return ; } if(vis[x]==true) { ans=min(ans,sum); return ; } if(sum>=dis[x][cnt]) { return ; } vis[x]=true; dis[x][cnt]=sum; for(int i=head[x];i!=0;i=e[i].next) { int u=e[i].to; dfs(u,sum+e[i].v,cnt+(e[i].f?1:0)); } vis[x]=false; } int main() { freopen("trolley.in","r",stdin); freopen("trolley.out","w",stdout); n=read();m=read();k=read(); for(int i=1;i<=n;i++) { int x=read(),y=read(),v=read(); add(x,y,v,false); } for(int i=1;i<=abs(m-n);i++) { int x=read(),y=read(),v=read(); add(x,y,v,true); } memset(dis,0x3f,sizeof(dis)); for(int i=1;i<=k;i++) { dis[0][i]=0; } dfs(1,0,0); cout<<ans<<endl; return 0; }
the end
撒花awa