一场3天前的cf

啊

这次的cf其实水的（指前4题）

题面就不给了awa
T1其实就是一个贪心，其实手模一下就好了。
可以发现，先让小的那个变大，然后在后面一直让小的加上大的
统计一下次数就是答案了。
因为如果是这样算的话，两次相加，大的那个数加上的数就是a+b，但是如果是单独加一个就是2b，b<a
所以得到了轮流加上这个数一定是更优的。

code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int a,b,n,T;
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    T=read();
    while(T--)
    {
        a=read();b=read();n=read();bool flag=0;
        int ans=0;
        while(a<=n&&b<=n)
        {
            if(a<=b)a+=b;
            else b+=a;
            ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}

 T2

就是找一个串，要求里面有>=n个的子串为"codeforces"，求这个子串

这个我题面忘记了。。。

T3

简单题，题面不描述了。。
我百度翻译一看。。。
发现它把1e9给我翻译成了109。。。

艹。。。
其实有一个方法能够构造出任意个数的答案，就是因为他能够一个一个的加，大概是这样的

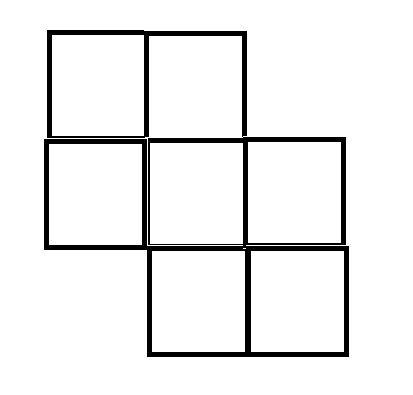
这种情况就是有一个的

下面的是两个的

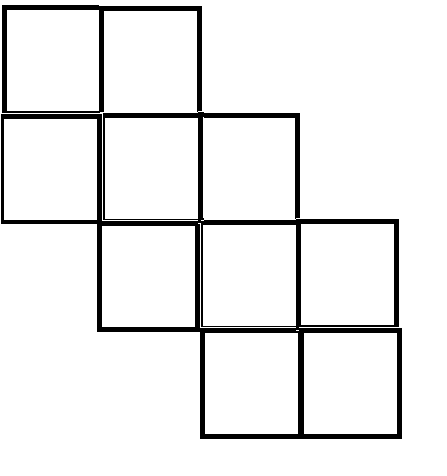
三个及以上的就直接以此类推就好了

这就是正解了。。。

就是因为那个109.。。
我自己想了好久。。。。
淦

code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n;
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read();
    int ans=4+3*n;
    cout<<ans<<endl;
    printf("0 0
0 1
1 0
");
    for(int i=1;i<=n;i++)
    {
        cout<<i<<' '<<i<<endl<<i<<' '<<i+1<<endl<<i+1<<' '<<i<<endl;
    }
    cout<<n+1<<' '<<n+1<<endl;
    return 0;
}

T4

其实这就是一个贪心。。。。

我还以为是个数位dp。。。

因为，可以发现，我们如果要做一次变化，那么肯定是要是其中一个数越大越好的

一个是|，一个是&，这个其实就是在把其中的1和零分开。

如果这两个数上的这两个为都是0，那的到的就是两个0

如果一个是一，一个是零，那么，就可以使1到一个数上，0到另一个数上，这两个数一个是富集1的，一个是富集零的

如果两个数都是1，那么就是两个1

所以我们只需要去统计1的数量就好了

code

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read() {
    char c = getchar();
    ll a = 0, b = 1;
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-')
            b = -1;
    for (; c >= '0' && c <= '9'; c = getchar()) a = a * 10 + c - 48;
    return a * b;
}
ll b[1000001], cnt[10000001], m, a[100001], sum, ans = 0, n;
int main() {
    n = read();
    for (ll i = 1; i <= n; i++) {
        a[i] = read();
        for (ll j = 0; j <= 20; j++) {
            if ((a[i] >> j) & 1)
                b[j]++;
        }
    }
    for (ll i = 1; i <= n; i++) {
        ll sum = 0;
        for (ll j = 0; j <= 20; j++) {
            if (b[j]) {
                sum |= (1 << j);
                b[j]--;
            }
        }
        ans += sum * sum;
    }
    cout << ans << endl;
    return 0;
}

 awa

这就是我写了的题目了