LeetCode 287

(Find the Duplicate Number/寻找重复数)[https://leetcode-cn.com/problems/find-the-duplicate-number/]

描述

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

说明

1.You must not modify the array (assume the array is read only).
2.You must use only constant, O(1) extra space.
3.Your runtime complexity should be less than O((n^2)).
4.There is only one duplicate number in the array, but it could be repeated more than once.

1.不能更改原数组（假设数组是只读的）。
2.只能使用额外的 O(1) 的空间。
3.时间复杂度小于 O((n^2)) 。
4.数组中只有一个重复的数字，但它可能不止重复出现一次。

样例

Input: [1,3,4,2,2]
Output: 2

Input: [3,1,3,4,2]
Output: 3

思路分析

其实这道题虽然写了说明，但不按照它的说明来，也是可以过的。
不考虑要求的话，本题还是很简单的，可以用计数法也可以排序做。但考虑要求1和要求2就麻烦了，不能改原数组、不能开新数组，直白看似乎应该暴力搜索，但暴力需要循环两次，时间复杂度O(n2)不满足要求3了。但注意到题目里“其数字都在 1 到 n 之间”的条件，关键也许就在这里。

二分法

从这个思路出发，我尝试用二分法来做。以n=5举例，比3小的数应该有2个，大于等于3的数应该有3个，如果数多了出来就说明重复数在那一半，之后不断二分就能找到重复数了，二分法的时间复杂度是O(nlogn)，符合所有要求。
虽然用这种方法AC了，但执行用时只战胜了8.94%的用户。还有一种更快的方法——快慢指针法

快慢指针法

快慢指针，顾名思义，一个移动快的指针，一个移动慢的指针。有什么用呢？一个常用的用途就是判断循环链表。快指针每次移动两格，慢指针一次移动一格，如果快指针追上了慢指针，就表示链表是循环的。此外还可以用来求单链表的中间点，当快指针到达链表尾部，慢指针所在位置就是链表的中间位置。那么，这道题该如何用呢？
考虑数组a=[1,3,4,2,2]，a[0]=1，a[1]=3……
其实不妨可以把数组理解成函数，数组下标是自变量，数组值是函数值，那么数组其实就是一组数和另一组数之间的映射。而这个函数a的值域是从1到n的，定义域是0到n，也就是说定义域包含值域，函数值可以继续映射，因此可以把数组变换成下面的链表形式：0->1->3->2->4->2。这就把数组改造成了链表。
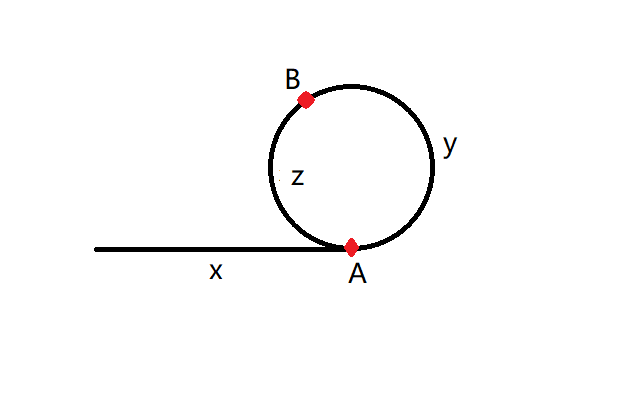
当然数组变成链表完全可以不用这样做，那么为什么要这么改造呢？我们再来考察这组链表，0->1->3->2->4->2，实际上它还可以继续链下去，2->4->2->4……因为它形成了一个环。因为重复数的存在，映射必然不是单射，链表必然形成一个环，而定义域包含值域，至少0不在值域中，因此这种变换必然是一段直线加上一个环，而交点就是要找的重复数（因为重复数是进入环的开端）。如果用快慢指针法，快慢指针必然在环内某点相遇，虽然我们希望相遇点就是环和直线的交点，但显然不成立，那么接下来我们如何找出交点呢？
不妨设直线部分的长度为x，环的开端A到快慢指针交点B的距离为y，点B到端点A的距离为z。考虑交点B的特性，有x+y+z+y=2*(x+y)，整理可得，x=z。
这个关系可不得了，这说明了交点到端点的距离与直线段的长度是相等的！因此，我们只需两个指针分别从交点和起始点开始，以单步长为1前进，他们的相遇点就是我们要求的端点A了。
很显然，这个方法是线性的，时间复杂度为O(n)，性能非常优异，也满足所有条件，代码也非常短。

代码

分治法，时间复杂度O(nlogn)

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        lnum = 1
        rnum = len(nums)
        while lnum+1 < rnum:
            snum = 0
            mnum = int((lnum+rnum)/2)
            for num in nums:
                if num < mnum and num >= lnum:
                    snum = snum + 1
            if snum > mnum-lnum:
                rnum = mnum
            else:
                lnum = mnum
        return lnum

快慢指针算法，时间复杂度O(n)

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        slow = nums[0]
        fast = nums[nums[0]]
        while slow != fast:
            slow = nums[slow]
            fast = nums[nums[fast]]
        fast = 0
        while nums[slow] != nums[fast]:
            slow = nums[slow]
            fast = nums[fast]
        return nums[slow]