刷题-力扣-304. 二维区域和检索

304. 二维区域和检索 - 矩阵不可变

题目链接

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problemset/all/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目描述

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

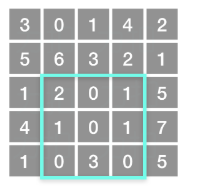
上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例：

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

提示：

• 你可以假设矩阵不可变。
• 会多次调用 sumRegion 方法。
• 你可以假设 row1 ≤ row2 且 col1 ≤ col2 。

题目分析

1. 根据题目描述获取范围内数字的总和
2. 私有成员变量matrix的第i行第j位，存储矩阵第i行0到j的总和
3. 获取区域内数字总和只需循环col2-col1+1次

代码

class NumMatrix {
private:
    vector<vector<int>> matrix;
public:
    NumMatrix(vector<vector<int>>& matrix) {
        vector<int> rowSum;
        for (int i = 0; i < matrix.size(); i++) {
            rowSum.clear();
            for (int j = 0; j < matrix[i].size(); j++) {
                rowSum.push_back(j == 0 ? matrix[i][j] : matrix[i][j] + rowSum[j - 1]);
            }
            this->matrix.push_back(rowSum);
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int row = row1; row <= row2; row++) {
            sum += col1 == 0 ? this->matrix[row][col2] : this->matrix[row][col2] - this->matrix[row][col1 - 1];
        }
        return sum;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */