刷题-力扣-221. 最大正方形

221. 最大正方形

题目链接

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-square/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

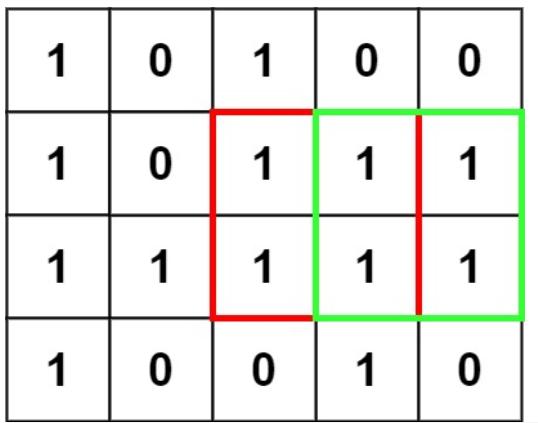
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

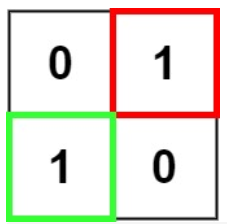
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

题目分析

1. 根据题目描述计算二维矩阵内最大的‘1’组成的正方形的面积
2. 假设f(x,y)表示以(x,y)结尾的正方形的维数，
   当matrix[x][y]=0时，f(x,y)=0
   当matrix[x][y]=1时，f(x,y)=min{f(x-1,y), f(x-1,y-1), f(x,y-1)}+1
3. 边界条件
   当x=0或y=0时，f(x,y)=matrix[x][y]

代码

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        int maxSquare = 0;
        for (int i = 0; i < m; ++i) {
            if (matrix[i][0] == '1') dp[i][0] = 1;
            maxSquare = max(dp[i][0], maxSquare);
        }
        for (int j = 0; j < n; ++j) {
            if (matrix[0][j] == '1') dp[0][j] = 1;
            maxSquare = max(dp[0][j], maxSquare);
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j]);
                    dp[i][j] = min(dp[i][j], dp[i][j - 1]) + 1;
                    maxSquare = max(dp[i][j], maxSquare);
                }
            }
        }
        return maxSquare * maxSquare;
    }
};