HDU 2150 Pipe
经过激烈的争夺,Lele终于把那块地从Yueyue的手里抢了回来。接下来,Lele要开始建造他的灌溉系统。
通过咨询Lele的好友——化学系的TT,Lele决定在田里挖出N条沟渠,每条沟渠输送一种肥料。
每条沟渠可以看作是一条折线,也就是一系列线段首尾连接而成(除了第一条线段开头和最后一条线段的结尾)。由于沟渠很细,你可以忽略掉它的宽度。
由于不同的肥料之间混合会发生化学反应,所以修建的沟渠与沟渠之间不能相交。
现在TT给Lele画了一些设计图,Lele请你判断一下设计图中的沟渠与沟渠之间是否有相交。
Input
本题目包含多组测试,请处理到文件结束(EOF)。
每组测试的第一行有一个正整数N(0<N<30),表示管道的数目。接下来给出这N条管道的信息。
对于每条管道,第一行是一个正整数K(0<K<100),表示这条管道是由K个端点组成。
接下来的K行给出这K个端点信息。每个端点占一行,用两个整数X和Y(0<X,Y<1000)分别表示这个端点的横坐标和纵坐标的值。
Output
对于每组测试,如果该测试管道与管道之间有相交的话,输出"Yes",否则输出"No"。
Sample Input
2
2
0 0
1 1
2
0 1
1 0
2
2
0 0
1 1
2
1 0
2 1
2
3
0 0
1 1
2 1
2
2 0
3 0
Sample Output
Yes
No
No
直接枚举每两个管道所有线段是否相交就可以了
判断线段是否相交
快速排斥实验 分别以两条线段 p1p2 ,Q1Q2 为两个矩形的对角线 ,如果两个矩形不相交,那么线段也一定不相交
跨立实验 如果两个线段相交,那么必然跨立,若 p1p2 跨立 Q1Q2 那么 p1点p2点 一定分别位于 线Q1Q2 的两侧,若不相交 ,那么一定位于同一侧,假设p1p2 跨立 Q1Q1,那么 { 向量(p1Q2)与向量(p1p2)的叉积 } 与 { 向量(p1p2) 与向量(p1Q1) } 的向量方向一定相同(根据叉积的右手定则判断),反之 Q1Q2跨立p1p2同理!
若叉积为0,说明共线
复习了一遍叉积,向量方向才搞明白。。
附上学习博客:https://blog.csdn.net/mikasa3/article/details/50833292
画图: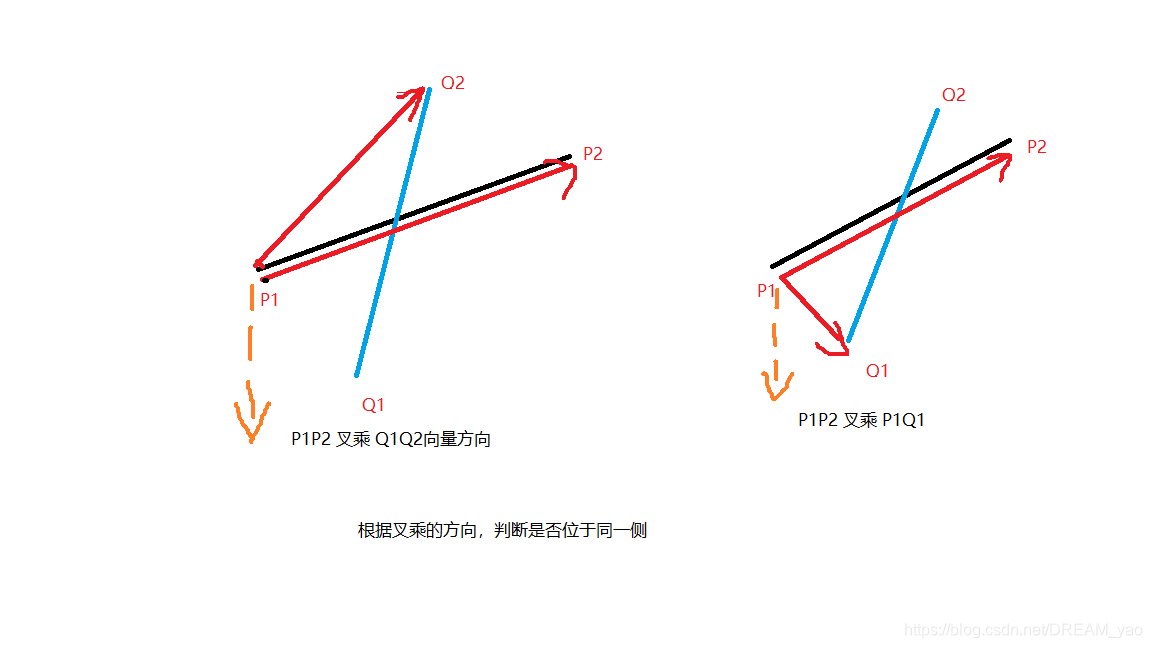
向量

撸代码:
/**判断折线段是否相交*/
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<iostream>
#include<string.h>
using namespace std;
struct Point
{
int x,y;
} p[35][105]; /*管道,端点*/
int n,k[35];
double xMul(Point a,Point b,Point c)/*向量ab 叉乘 ac*/
{
return (a.x-b.x)*(a.y-c.y)-(a.y-b.y)*(a.x-c.x);/*两种都可以*/
//return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
bool judge(Point a,Point b,Point c,Point d)/*判断a->b,c->d 是否相交*/
{
if(max(a.x,b.x)>=min(c.x,d.x)&&/*判断两矩形相交,快速排斥实验*/
max(c.x,d.x)>=min(a.x,b.x)&&
max(a.y,b.y)>=min(c.y,d.y)&&
max(c.y,d.y)>=min(a.y,b.y)&&
xMul(a,b,c)*xMul(a,d,b)>=0&&/*跨立实验*/
xMul(c,a,d)*xMul(c,d,b)>=0)
return 1;
return 0;
}
int main()
{
while(~scanf("%d",&n))
{
memset(k,0,sizeof(k));
for(int i=0; i<n; i++)
{
scanf("%d",&k[i]);
for(int j=0; j<k[i]; j++)
{
scanf("%d%d",&p[i][j].x,&p[i][j].y);
}
}
if(n==1)
{
printf("No
");
continue;
}
int flag=0;
for(int i=0; i<n-1; i++) /*枚举每个管道是否与其他管道相交*/
for(int u=1; u<k[i]; u++)
{
for(int j=i+1; j<n; j++)
for(int v=1; v<k[j]; v++)
{
if(judge(p[i][u-1],p[i][u],p[j][v-1],p[j][v]))
{
flag=1;
break;
}
}
}
if(flag)
{
printf("Yes
");
}
else
{
printf("No
");
}
}
return 0;
}