貌似是第一篇没咕的题解呢
Problem A.
题意
给定一个数x,要求构造两个正整数a,b,使得gcd(a,b)+lcm(a,b)=x。(x<=1e9)
解法
简单构造,a=1,b=x-1即符合题目要求。
代码
#include <bits/stdc++.h> using namespace std; int T, n; int main () { scanf ("%d", &T); while (T --) { scanf ("%d", &n); printf ("%d %d ", 1, n - 1); } return 0; }
Problem B.
题意
给定一个数组a1,a2,a3,……,an,把这个数组复制n遍(即a1,a2,……,an,a1,a2,……,an,a1,……),求新数组的最长上升子序列长度。
解法
分析一下,假设原数组剔除掉重复的数后有m个元素,则最长上升子序列的长度不可能超过m(若选择超过m个数肯定会有重复,不符合最长上升子序列的定义)。对从前往后第i个数组取该数组第i大的数即可构造出有m个数的最长上升子序列。
故始终有最长上升子序列长度为m的解存在。
代码
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; int T, n, a[N]; int main () { scanf ("%d", &T); while (T --) { scanf ("%d", &n); map <int, bool> mp; int ans = 0; for (int i = 1; i <= n; i ++) { scanf ("%d", &a[i]); if (!mp[a[i]]) ans ++; mp[a[i]] = true; } printf ("%d ", ans); } return 0; }
Problem C.
题意
题面写的什么辣鸡玩意,花了45min看题5min想题3min写题1min调题
给定一颗有n个节点n-1条边的树,要求在所有边上标上0、1、2、……、n-2,定义MEX(u,v)为该树上除u到v的简单路径要经过的边除外的树上所有边的值中的最小值,使得对于任意的u,v的MEX(u,v)的最大值尽可能地小。
再解释一遍MEX的定义:

这是题目给定的样例中的树。
假设我们要求MEX(4,6)。
先求出4->6的简单路径:
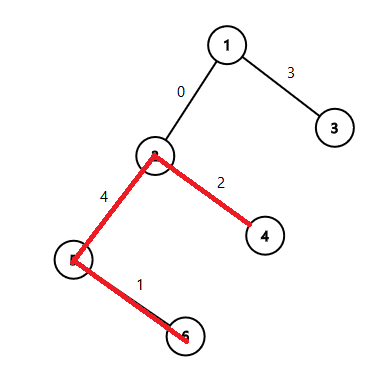
可以看出,该路径经过了1、2、4三边,则该树剩下的边为0、3,其中最小值为0,故MEX(4,6)即为0。
同理可得,MEX(4,3)=1,MEX(3,6)=2。
解法
显然,树上的任意一条从一个点到另一个点的简单路径不会经过同一个点两次,等价于不会经过任何与同一个点连接的三条边。
由此可以构造出一棵答案最小的树:寻找一条与三条及以上的边连接的点,将与该点连接的任意三条边赋值为0、1、2。
因为0、1、2三条边不可能同时存在于一条简单路径上,所以答案为2。又因为一棵树上任意两条边都可以存在于一条简单路径上,故答案不可能大于2。
可以发现,此构造最优。
代码
注意特判树为一条链的情况。
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; int n, m, chose, ans[N], tim, cnt = 3, visit[N]; vector <int> g[N]; pair <int, int> p[N]; int main () { scanf ("%d", &n); for (int i = 1; i < n; i ++) { int u, v; scanf ("%d %d", &u, &v); g[u].push_back (v); g[v].push_back (u); p[i].first = u; p[i].second = v; } for (int i = 1; i <= n; i ++) if (g[i].size() >= 3) { chose = i; break; } if (chose == 0) { for (int i = 1; i < n; i ++) printf ("%d ", i - 1); return 0; } for (int i = 1; i < n; i ++) if (p[i].first == chose || p[i].second == chose) { ans[i] = tim; tim ++; visit[i] = 1; if (tim > 2) break ; } for (int i = 1; i < n; i ++) if (!visit[i]) ans[i] = cnt ++; for (int i = 1; i < n; i ++) printf ("%d ", ans[i]); return 0; }
Problem D.
题意
构造一个尽可能短的长度为n的数组,使得该数组所有元素的和为给定值v,所有元素异或和为给定值u。
解法
三题构造就**离谱
第一步先判断u,v是否有解。
若干数的异或和必定不大于它们的和,故v应不小于u。
其次,若异或和的个位为1,则该数组中,个位为1的个数必为奇数,则和的个位也应为1。同理,若异或和的个位为0,则和的个位也应为0。
所以,当且仅当v>=u且(v-u)|2的情况下,u、v有解。
显然,在u、v有解的情况下,{u,(v-u)/2,(v-u)/2}是一种始终有解的构造,所以我们只需要考虑特判n<3的情况。
n=0:在u=v=0的情况下有解。
n=1:在u=v的情况下有解。
n=2:在{(v+u)/2、(v-u)/2}满足条件的情况下成立。(具体原因不写了会写在另一篇博客里)
代码
#include <bits/stdc++.h> using namespace std; long long n, m; int main () { scanf ("%lld %lld", &n, &m); if (n > m || (m - n) % 2 != 0) { puts ("-1"); return 0; } else if (n == m && n == 0) { puts ("0"); } else if (n == m) { printf ("1 %lld", n); } else { long long x = (n + m) / 2, y = n; long long a = x, b = x - y; if ((a + b) == m && (a ^ b) == n) printf ("2 %lld %lld", a, b); else printf ("3 %lld %lld %lld", n, (m - n) / 2, (m - n) / 2); return 0; } return 0; }