关于A Star Algorithm
A star算法最早可追溯到1968年,在IEEE Transactions on Systems Science and Cybernetics中的一篇A Formal Basis for the Heuristic Determination of Minimum Cost Paths,是把启发式方法(heuristic approaches)如BFS,和常规方法如Dijsktra算法结合在一起的算法。有点不同的是,类似BFS的启发式方法经常给出一个近似解而不是保证最佳解。然而,尽管A star基于无法保证最佳解的启发式方法,A star却能保证找到一条最短路径。
公式表示为:f(n)=g(n)+h(n)
f(n)是节点n从初始点到目标点的估价函数
g(n)是在状态空间中从初始节点到n节点的实际代价
h(n)是从n到目标节点最佳路径的估计代价
观察A*寻路算法的运行轨迹
假设起点为A(浅蓝色的个字) 终点为B(深蓝色的格子)
红色代表该格子为障碍物
地图为20x20的格子
显示FGH值的格子代表经过A*算法搜索并生成路径的格子
有透明度变化的格子代表该格子有被搜索。
绿色格子代表的是搜索完成后A*得到的最优的路径
A直接抵达B的情况下

A越过直线障碍到达B

A越过U型障碍到达B

B为障碍物所包围着,A到达不了B的情况下

总结与思考
由4组图可以得到
1.A*的消耗是一个及其不稳定的过程,消耗的最小值不低于直线路径上的消耗,消耗的最大值不高于遍历整张地图的消耗。
2.A*的消耗主要在搜索的搜索格子,以及对其FGH的操作上。
3.由1,2可以得出,在对运行速率和效率有要求的场景下,A*可能不是一个比较好选择。
算法步骤
横向纵向的格子的单位消耗为10,对角单位消耗为14。
定义一个OpenList,用于存储和搜索当前最小值的格子。
定义一个CloseList,用于标记已经处理过的格子,以防止重复搜索。
开始搜索寻路
1.将起点加入OpenList
2.从OpenList中弹出F值最小的点作为当前点
3.获取当前点九空格(除去自己)内所有的非障碍且不在CloseList内的邻居点
4.遍历上一步骤得到的邻居点的集合,每个邻居点执行以下逻辑
如果邻居点在OpenList中
计算当前值的G与该邻居点的G值
如果G值比该邻居点的G值小
将当前点设置为该邻居点的父节点
更新该邻居点的GF值
若不在
计算并设置当前点与该邻居点的G值
计算并设置当前点与该邻居点的H值
计算并设置该邻居点的F值
将当前点设置为该邻居点的父节点
5.判断终点是否在OpenList中,如果已在OpenList中,则返回该点,其父节点连起来的路径就是A*搜索的路径。如果不在,则重复执行2,3,4,5。直到找到终点,或者OpenList中节点数量为0。
Tip:判定结束的有两种
第一种是以OpenList中有终点节点或者OpenList中没有节点
第二种是CLoseList中有终点节点或者......
第一种要比第二种运算次数要少许多,但在最短路径的的处理上,第二种要比第一种要精准,是相对精准。
图解算法
(7,10)为起点 ,(11,10)为终点,(9,11) (9,10)(9,9)为障碍点。
1.当前点为(7,10)
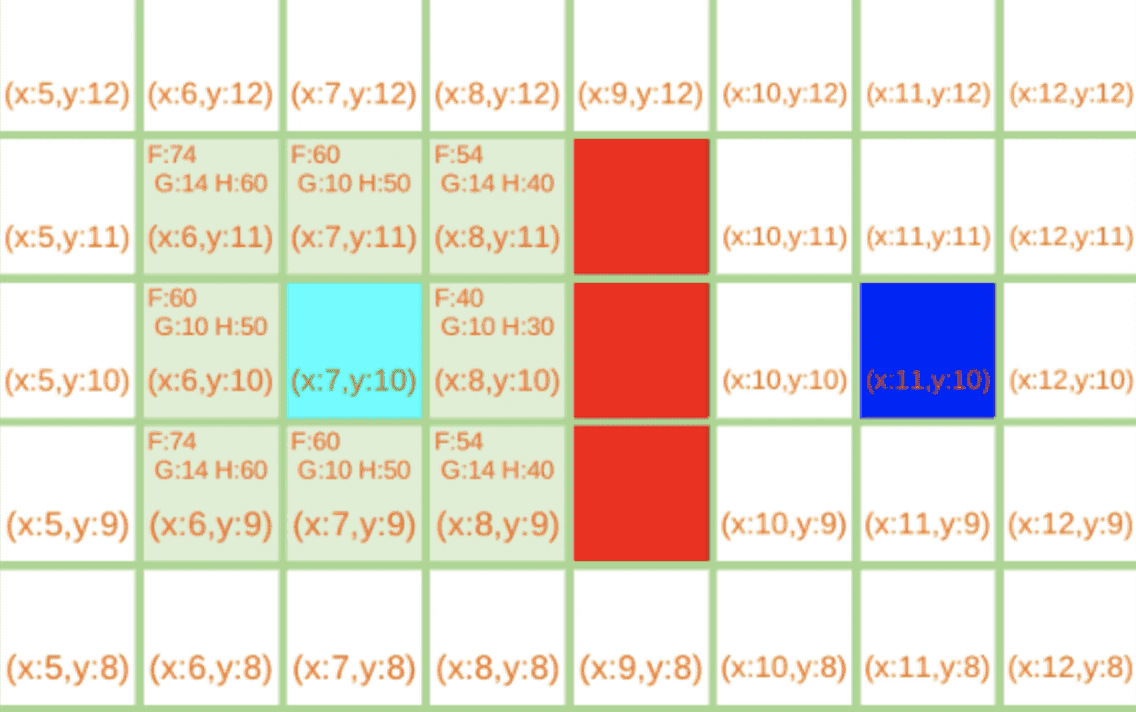
2.当前点为(8,9)
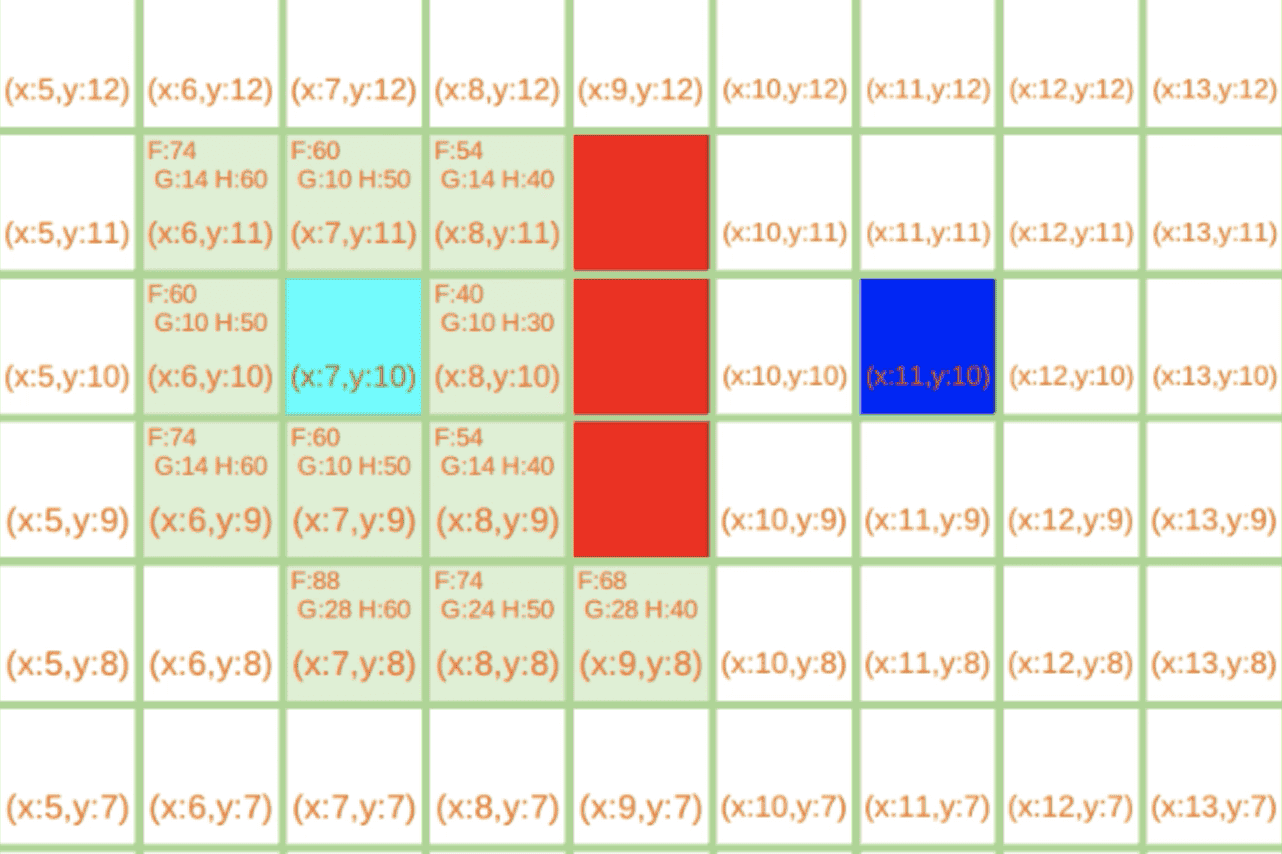
2.当前点为(8,11)
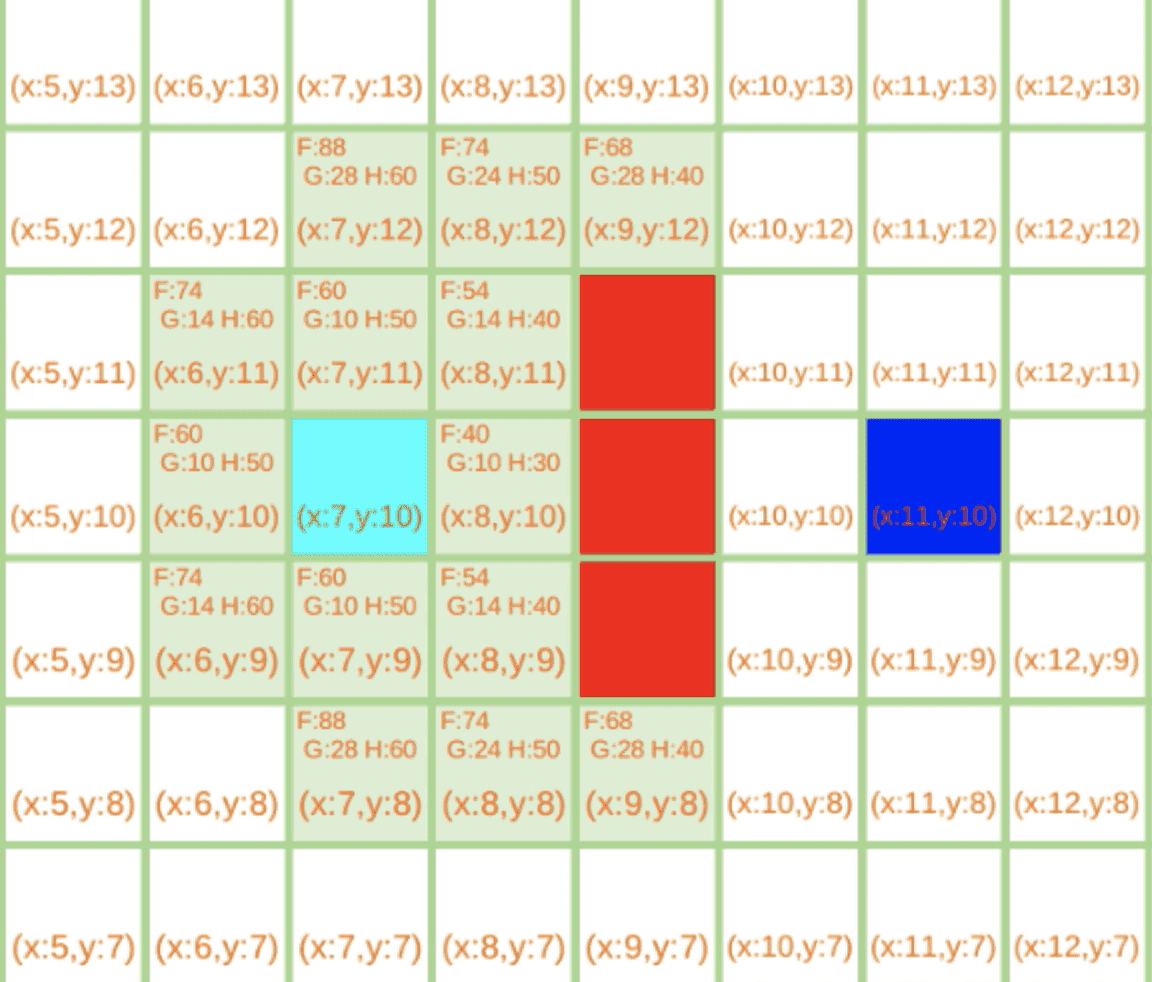
当前点为(6,10)
这里是最容易忽视的地方,因为A*的启发搜索的实现就是靠搜索F值最小的节点来实现,所以是会出现这种背离目标的搜索。

当前点为(7,9)

当前点为(7,11)

当前点为(9,8)

当前点为(10,9)
当OpenList中出现终点节点时,则结束此次搜索
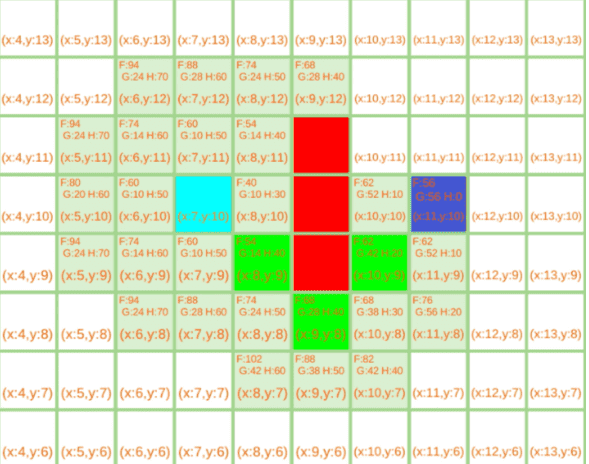
如果有想看更复杂的条件下的搜索轨迹,在线的AStarDemo 或者clone github工程
总结与思考
A的消耗有很大的不确定性。消耗跟地图的复杂程度成正比,跟相对距离的长短成正比。
有一个极端的情况,当终点位置为障碍点包围时,即A Star找不到终点坐标,A会遍历该地图此障碍区以外的所有区域。
关键逻辑的代码实现
1.A*寻路算法的主逻辑
Point start = ...;
Point end = ...;
bool isIgnoreCorner = ...;
OpenList.Add(start);
while (OpenList.Count != 0)
{
stepSearch(start, end, isIgnoreCorner);
if (OpenList.Get(end) != null)
return OpenList.Get(end);
}
return OpenList.Get(end);
2.单次搜索所执行的逻辑
//找出F值最小的点
var tempPoint = OpenList.PopMinPoint();
//OpenList.RemoveAt(0);
CloseList.Add(tempPoint);
var alivePoints = GetGridAlivePoint(tempPoint, isIgnoreCorner);
for (int i = 0; i < alivePoints.Count; i++)
{
Point p = alivePoints[i];
if (OpenList.Exists(p))
{
//计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和F
FoundPoint(tempPoint, p);
}
else
{
//如果它们不在开始列表里, 就加入, 并设置父节点,并计算GHF
NotFoundPoint(tempPoint, end, p);
}
}
3.当邻居点在OpenList点中时的处理逻辑
var G = CalcG(tempStart, point);
if (G < point.G)
{
point.ParentPoint = tempStart;
//因为每次取值,都是使用F值,所以我觉的可以不更新G值
//point.G = G;
point.F = point.H + G;
}
4.当邻居点不在OpenList点中时的处理逻辑
point.ParentPoint = tempStart;
point.G = CalcG(tempStart, point);
point.H = CalcH(end, point);
point.CalcF();
OpenList.Add(point);
5.最基础的逻辑也是最重要的逻辑之一,计算G值
计算G值 只适用于相邻的两个点
int G = (Math.Abs(point.X - start.X) + Math.Abs(point.Y - start.Y)) == 2 ? 14:10;
int parentG = point.ParentPoint != null ? point.ParentPoint.G : 0;
return G + parentG;
5.最基础的逻辑也是最重要的逻辑之一,计算H值
同G值,这里只计算直线上的消耗,不处理对角。
int step = Math.Abs(point.X - end.X) + Math.Abs(point.Y - end.Y);
return step * 10;
应用与思考
1.A* 在游戏中多有应用,怪物AI,计算玩家行走的路径,一些辅助工具比如游戏机器人玩家的策略方案等应用。但因为其消耗的极其不稳定,所以不会作为首选,在游戏中如果大量的应用这种逻辑,JPS(Jump Search Point),或者JPS+(JPS的优化版本)
2.A*在AR和自动驾驶领域也有应用。比如有些AR的应用是基于SLAM算法进行场景实时建模,然后在生成的模型当中,搜索一条有效的路径。A Star在这种场景中有很强的应用空间。
3.A Star的消耗主要是不断的搜索生成新的节点,不断的遍历计算。其优化思路一般也是围绕这两个点,减少搜索次数,优化遍历方案。我个人觉得JPS(Jump Point Search )就是把A Star优化做到一定程度的结果。
4.第一篇关于A Star文章是在1968年,第一篇关于JPS的文章是在2011年。在这段时间A Star处于什么样的一个地位,在这期间A Star又经历了什么样的演变,又演变出多少种在其基础之上优化的算法。在我看来刚出世时的A Star是一种算法,一种工具,在经历种种反复的推敲之后,俨然成为了一种思想,一种在未知领域寻找最优解的思想。