BZOJ#4237. 稻草人

4237: 稻草人

Time Limit: 40 Sec Memory Limit: 256 MB
Submit: 1483 Solved: 649
[Submit][Status][Discuss]

Description

JOI村有一片荒地，上面竖着N个稻草人，村民们每年多次在稻草人们的周围举行祭典。

有一次，JOI村的村长听到了稻草人们的启示，计划在荒地中开垦一片田地。和启示中的一样，田地需要满足以下条件：

田地的形状是边平行于坐标轴的长方形；

左下角和右上角各有一个稻草人；

田地的内部(不包括边界)没有稻草人。

给出每个稻草人的坐标，请你求出有多少遵从启示的田地的个数

Input

第一行一个正整数N，代表稻草人的个数

接下来N行，第i行(1<=i<=N)包含2个由空格分隔的整数Xi和Yi，表示第i个稻草人的坐标

Output

输出一行一个正整数，代表遵从启示的田地的个数

Sample Input

4
0 0
2 2
3 4
4 3

Sample Output

HINT

所有满足要求的田地由下图所示：

1<=N<=2*10^5

0<=Xi<=10^9(1<=i<=N)

0<=Yi<=10^9(1<=i<=N)

Xi(1<=i<=N)互不相同。

Yi(1<=i<=N)互不相同。

题目大意：

二维坐标系中给定了一些点，求两两组合构成矩形，满足一个在右上角，一个在左下角，并且他们中间没有其他点，求对数

分析：

二维偏序，考虑CDQ分治

我们分治时，先把y排序，分成上部分和下部分

再分别上下部分，按照x排序

现在我们的上部分的y都大于下部分的y

两部分的x都是有序的

我们再用栈维护上部分的y递增

用栈维护下部分的y递减

现在

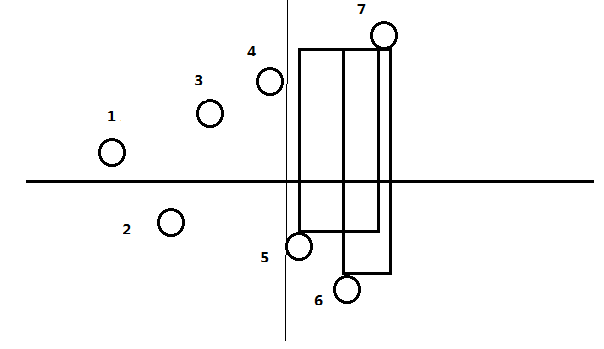
这样的我们枚举维护上部分

同时维护下部分下部分x不超过当前上部分的x

比如上图，我们上部分维护到了7

下部分也维护到了6

我们发现4之后的下部分的栈里面的数都可以和7组成矩形且中间没有点

(因为我们维护了下部分递减，所以中间不会再出现比他们小的数，有的话 5也会被弹出栈)

但是4前面的点，和7组成矩形，中间一定会有4，所以是不满足的

所以我们就二分找出第一个x大于的下部分点

ans+=top2-res+1

加上这些点的个数就是答案了

现在我们就解决了上下组合的问题

剩下的问题继续CDQ分治解决

附上代码：

#include<bits/stdc++.h>
using namespace std;
int n;
struct node{int x,y;}d[200010],b[200010];
int cmpx(node a,node b) {return a.x<b.x;}
int cmpy(node a,node b) {return a.y<b.y;}

long long ans;
int temp1,temp2,stack1[200010],stack2[200010];

int find(int x,int l,int r){  
    while (l+1<r){  
        int mid=(l+r)>>1;  
        if (d[stack2[mid]].x<x) l=mid; else r=mid;  
    }  
    return l;  
}  

void CDQ(int l,int r)
{
    if(l==r) return ;
    int mid=(l+r)>>1;
    CDQ(l,mid);CDQ(mid+1,r);
    temp1=0,temp2=0;

    int j=l;
    for(int i=mid+1;i<=r;i++) 
    {
        while(temp1&&d[stack1[temp1]].y>d[i].y) temp1--;//上部分维护y递增 
        stack1[++temp1]=i;
        while(j<=mid&&d[j].x<d[i].x) 
        {
            while(temp2&&d[stack2[temp2]].y<d[j].y) temp2--;//下部分维护y递减  
            stack2[++temp2]=j;
            j++;
        }
        int st=d[stack1[temp1-1]].x;//前面一个点的位置 
        int L=1,R=temp2,res=-1;
    
        while (L<=R)
        {  
            int mid=(L+R)/2;  
            if(d[stack2[mid]].x<st) L=mid-1;
            else res=mid,R=mid-1;
        } 
        if(res!=-1) ans+=temp2-res+1;//二分出来这个点 后面的点都满足 
    }
    j=l;int k=mid+1;  
    for (int i=l; i<=r; i++)  
    b[i]=(j<=mid && d[j].x<d[k].x || k>r)?d[j++]:d[k++];  
    for (int i=l; i<=r; i++) d[i]=b[i];  
}

int main()
{
    freopen("a.in","r",stdin);
    
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&d[i].x,&d[i].y);
    sort(d+1,d+n+1,cmpy);
    CDQ(1,n);
    printf("%lld
",ans);
    return 0;
}

View Code

多一个log

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
struct node {int x,y;}d[N];
int n,stack1[N],top1,stack2[N],top2;
long long ans=0;
inline bool cmpy(node a,node b) {return a.y<b.y;}
inline bool cmpx(node a,node b) {return a.x<b.x;}

void CDQ(int l,int r)
{
    if(l==r) return ;
    int mid=(l+r)>>1;
    top1=top2=0;
    sort(d+l,d+r+1,cmpy);
    sort(d+l,d+mid+1,cmpx);
    sort(d+mid+1,d+r+1,cmpx);
    
    int j=l;
    for(int i=mid+1;i<=r;i++) 
    {
        while(top1&&d[stack1[top1]].y>=d[i].y) top1--;//上部分维护y递增 
        stack1[++top1]=i;
        while(j<=mid&&d[j].x<d[i].x) 
        {
            while(top2&&d[stack2[top2]].y<=d[j].y) top2--;//下部分维护y递减  
            stack2[++top2]=j;
    m        j++;
        }
        int st=d[stack1[top1-1]].x;//前面一个点的位置 
        int L=1,R=top2,res=-1;
        while(L<=R) 
        {
            int mid=(L+R)>>1;
            if(d[stack2[mid]].x>st) res=mid,R=mid-1;
            else L=mid+1;
        }
        if(res!=-1) ans+=top2-res+1;//二分出来这个点 后面的点都满足 
    }

    CDQ(l,mid);CDQ(mid+1,r);    
}

int main()
{
    freopen("a.in","r",stdin);
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&d[i].x,&d[i].y);
    d[0].x=-1;d[0].y=-1;
    
    CDQ(1,n);
    printf("%lld
",ans);
    return 0;
}

View Code