BZOJ#1101. Zap

---

1101: [POI2007]Zap

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 3052  Solved: 1348

Description

　　FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a
，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

Input

　　第一行包含一个正整数n，表示一共有n组询问。（1<=n<= 50000）接下来n行，每行表示一个询问，每行三个
正整数，分别为a,b,d。（1<=d<=a,b<=50000）

Output

　　对于每组询问，输出到输出文件zap.out一个正整数，表示满足条件的整数对数。

Sample Input

2
4 5 2
6 4 3

Sample Output

3
2
//对于第一组询问，满足条件的整数对有(2,2)，（2,4），（4，2）。对于第二组询问，满足条件的整数对有（
6,3），（3,3）。

 

---

problem:

求gcd(a,b)==c (a<=n&&b<=m)的组数

 

---

solution：

感觉很套路了

推导：

　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　

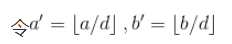
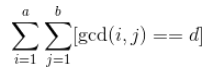
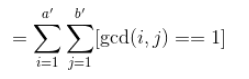
用莫比乌斯函数的性质把gcd换掉：

　　　　　　　　　　　　　　　　

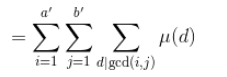
这一步的是意思是，如果gcd(i,j)不为一，那Σμ(d)就为0，否则为1刚好符合我们的需求

　　　　　　　　　　　　　　　 

 

按取值分成个段分别处理，一个连续段内的和可以用预处理出的莫比乌斯函数前缀和求出

 

---

附上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+12;
int mu[N],prime[N],cnt,vis[N];
int sum[N];
void getmu()
{
    mu[1]=1;
    for(int i=2;i<=N;i++)
    {
        if(!vis[i]) prime[++cnt]=i,mu[i]=-1;
        for(int j=1;j<=cnt;j++)
        {
            if(i*prime[j]>N) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) {mu[i*prime[j]]=0;break;}
            else mu[i*prime[j]]=-mu[i];
        }
    }
    for(int i=1;i<=N;i++) sum[i]=sum[i-1]+mu[i];
}
int main()
{
    getmu();
    int T;scanf("%d",&T);
    int n,m,D;
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&D);
        if(n>m) swap(n,m);
        int j=0;n/=D;m/=D;
        int ans=0;//开long long要挂 我也不知道为什么
        for(int i=1;i<=n;i=j+1)
        {
            j=min(n/(n/i),m/(m/i));
            ans+=(sum[j]-sum[i-1])*(n/i)*(m/i);
        }
        printf("%d
",ans);
    }
     
    return 0;
}