BZOJ#3529. [Sdoi2014]数表

3529: [Sdoi2014]数表

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 2566  Solved: 1325

Description

有一张 n×m 的数表，其第 i 行第 j 列（1 <= i <= n, 1 <= j <= m）的数值为

能同时整除 i 和 j 的所有自然数之和。给定 a , 计算数表中不大于 a 的数之和。

Input

输入包含多组数据。

输入的第一行一个整数Q表示测试点内的数据组数

接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

1 < =N．m < =10^5  ， 1 < =Q < =2×10^4

Output

对每组数据，输出一行一个整数，表示答案模2^31的值。

Sample Input

2
4 4 3
10 10 5

Sample Output

20
148

 

---

problem：

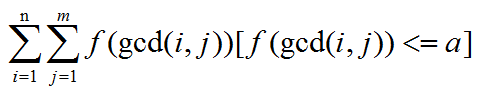
solution：

推导：

设f(d)为d的约数和:

            　　  　      

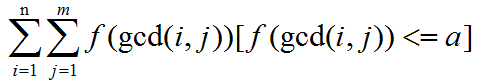
枚举gcd：

　　　　　　　　　　 

根据公式二套路：

　　　　　　　　　  　

                            

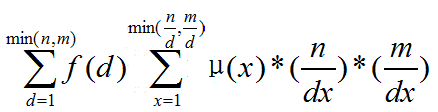
套路枚举dx：

　　　　　　　　    　

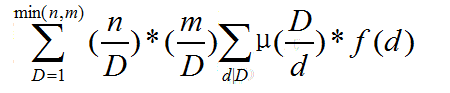
预处理出：

　　　　　　　　   　　　

                                                    

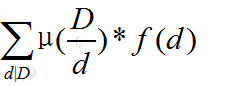
因为有a的限制

我们离线按a从小到大

我们用树状数组来限制f的值：

 

   for(int i=1;i<=T;i++)
    {
        for(;j<=N&&h[j].first<=q[i].a;j++)     //单个表格不超过a 因为h[j].first就是表示gcd(a,b)=j的格子的值
            for(int k=h[j].second;k<=N;k+=h[j].second)
            add(k,h[j].first*mu[k/h[j].second]);
        
        ans[q[i].id]=Query(q[i].n,q[i].m);
    }

---

附上代码：

 

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+12;
int mu[N],vis[N],prime[N],cnt;
void getmu()
{
    mu[1]=1;
    for(int i=2;i<=N;i++)     
    {
        if(!vis[i]) prime[++cnt]=i,mu[i]=-1;
        for(int j=1;j<=cnt;j++)
        {
            if(i*prime[j]>N) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) {mu[i*prime[j]]=0;break;}
            mu[i*prime[j]]=-mu[i];
        }
    }    
}
struct H
{
    int first,second;
    bool operator < (const H & other) const
    {
        return first < other.first;
    }
}h[N];
void geth()
{
    for(int i=1;i<=N;i++)
        for(int j=i;j<=N;j+=i)
        h[j].first+=i;    
    for(int i=1;i<=N;i++)
        h[i].second=i;
    sort(h+1,h+N+1);
}
struct Ask
{
    int n,m,a,id;
    bool operator < (const Ask & other )const
    {
        return a<other.a;
    }
}q[N];

int c[N];
inline int lowbit(int x) {return x&(-x);}
void add(int a,int b)
{
    while(a<=N)
    {
        c[a]+=b;
        a+=lowbit(a);
    }
}
int sum(int a)
{
    int s=0;
    while(a>0)
    {
        s+=c[a];
        a-=lowbit(a);
    }
    return s;
}
int Query(int n,int m)
{
    int ans=0,pos=0;
    if(n>m) swap(n,m);
    for(int i=1;i<=n;i=pos+1)
    {
        pos=min(n/(n/i),m/(m/i));
        ans+=(n/i)*(m/i)*(sum(pos)-sum(i-1));
    }
    ans&=0x7fffffff;
    return ans;
}
int ans[N];
int main()
{
    freopen("a.in","r",stdin);
    getmu();
    geth();
    int T;
    scanf("%d",&T);
    for(int i=1;i<=T;i++) scanf("%d%d%d",&q[i].n,&q[i].m,&q[i].a),q[i].id=i;
    sort(q+1,q+T+1);
    int j=1;
    for(int i=1;i<=T;i++)
    {
        for(;j<=N&&h[j].first<=q[i].a;j++)     //单个表格不超过a 因为h[j].first就是表示gcd(a,b)=j的格子的值
            for(int k=h[j].second;k<=N;k+=h[j].second)
            add(k,h[j].first*mu[k/h[j].second]);
        
        ans[q[i].id]=Query(q[i].n,q[i].m);
    }
    for(int i=1;i<=T;i++) printf("%d
",ans[i]);
    return 0;
}

---