椭圆曲线算数原理与实现

椭圆曲线算术理论基础

编程实现ECC模N意义下的点加法

首先分别是计算整数x、小数x对于模数N的乘法逆元的函数：

# based on extended Euclidean algorithm
# calc : x^(-1) mod N | x is int type 
# show=True means print calculate message
def IntModInverse(x, N, show = True):
    if gcd(N,x) != 1:
        return None
    if x == 1:
        return 1
    A1, A2, A3 = 1, 0, N
    B1, B2, B3 = 0, 1, x
    if show:
        print('-'*54)
        print("|{:^5}	{:^5}	{:^5}	{:^5}	{:^5}	{:^5}	{:^5}|".format("Q","A1","A2","A3","B1","B2","B3"))
        print("|{:^5}	{:^5}	{:^5}	{:^5}	{:^5}	{:^5}	{:^5}|".format("-", A1, A2, A3, B1, B2, B3))
    while True:
        Q = A3//B3
        B1,B2,B3,A1,A2,A3 = (A1-Q*B1),(A2-Q*B2),(A3-Q*B3),B1,B2,B3
        if show:
            print("|{:^5}	{:^5}	{:^5}	{:^5}	{:^5}	{:^5}	{:^5}|".format(Q, A1, A2, A3, B1, B2, B3))
        if B3 == 0:
            return None
        elif B3 == 1:
            break
    if show:
        print("-"*54)
    return B2 % N

# x is float type
def FloatModReverse(x, N, self = False):
    i = 1
    while True:
        if i*x % N == 1:
            break
        i += 1
    i %= N
    if not self: # 返回小数x关于模数N的逆元
        return i
    else:        # 返回小数x关于N的等价整数
        return IntModInverse(i, N, False)

比如计算1.5关于23的整数等价模，易知1.5 *（2/3）= 1 mod 23，而36 *（2/3）= 24 = 1 mod 23， 因此1.5 = 36 = 13 mod 23 。
其次是ECC点加的计算公式，得到的delta可能是小数，需要用上述定义的FloatModReverse函数。

# y^2 mod q == (x^3 + ax + b) mod q 
def ECC_Add(point1, point2, q, a, b):
    (x1, y1) = point1
    (x2, y2) = point2 
    if point1 == point2:
        delta = (3 * pow(x1, 2) + a)/(2 * y1)
        delta = FloatModReverse(delta, q, True) 
    else:
        delta = (y2 - y1)/(x2 - x1)
        delta = FloatModReverse(delta, q, True) 
    x3 = (pow(delta, 2) - x1 - x2) % q 
    y3 = (delta * (x1 - x3) - y1) % q
    return (x3, y3)

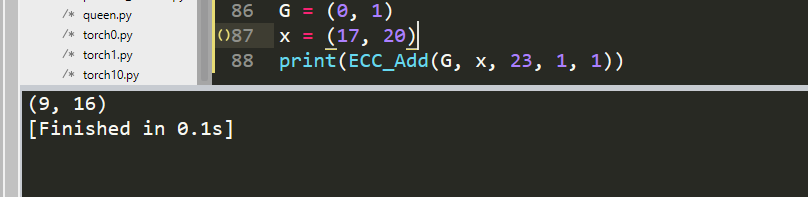
测试

G = (0, 1)
x = (17, 20)
print(ECC_Add(G, x, 23, 1, 1))

实数域上的ECC点加法，就是去除模N的限制，点坐标包含浮点数

# y^2 == (x^3 + ax + b)
def ECC_Add2(point1, point2, a, b):
    (x1, y1) = point1
    (x2, y2) = point2 
    if point1 == point2:
        delta = (3 * pow(x1, 2) + a)/(2 * y1)
        # print("delta:", delta)
    else:
        delta = (y2 - y1)/(x2 - x1)
        # print("delta:", delta)
    x3 = pow(delta, 2) - x1 - x2
    y3 = delta * (x1 - x3) - y1
    return (x3, y3)
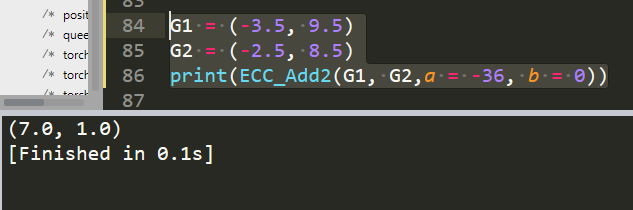
G1 = (-3.5, 9.5)
G2 = (-2.5, 8.5)
print(ECC_Add2(G1, G2,a = -36, b = 0))

效果

进一步，定义ECC模N意义下的点乘法

def ECC_Mul(point, n, q, a, b, show = True):
    (x, y) = point
    res = point
    for i in range(2, n+1):
        res = ECC_Add(point, res, q, a, b)
        if show:
            print("{} * G = {}".format(i, res))
    return res

G = (2, 7)
ECC_Mul(G, 12, q = 11, a = 1, b = 6)

返回结果点坐标，开启show会把计算过程全部展示出来（可继续优化）。

效果

其他参考

https://www.cnblogs.com/Kalafinaian/p/7392505.html
https://www.jianshu.com/p/96bbe37ce14d