Description
There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment.
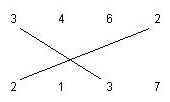
We want to find the maximum number of matching segments possible to draw for the given input, such that:
1. Each a-matching segment should cross exactly one b-matching segment, where a != b .
2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed.
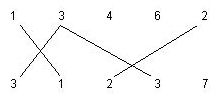
Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

We want to find the maximum number of matching segments possible to draw for the given input, such that:
1. Each a-matching segment should cross exactly one b-matching segment, where a != b .
2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed.

Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.
Input
The first line of the input is the number M, which is the number of test cases (1 <= M <= 10). Each test case has three lines. The first line contains N1 and N2, the number of integers on the first and the second row respectively. The next line contains N1 integers which are the numbers on the first row. The third line contains N2 integers which are the numbers on the second row. All numbers are positive integers less than 100.
Output
Output should have one separate line for each test case. The maximum number of matching segments for each test case should be written in one separate line.
Sample Input
3 6 6 1 3 1 3 1 3 3 1 3 1 3 1 4 4 1 1 3 3 1 1 3 3 12 11 1 2 3 3 2 4 1 5 1 3 5 10 3 1 2 3 2 4 12 1 5 5 3
Sample Output
6 0 8
题目大意:就是找出相等的两个数连接起来,但是线段还要和一条匹配线段相交;
求最大的匹配数;
解题思路:f[i][j],表示i,j前的最大匹配数;
当a[i]==b[j]的时候,考虑到前i个数和j-1个数的最大匹配数,以及前i-1个数和j个数的最大匹配数;
当a[i]!=b[j]的时候,那么应该是max{f[p-1][q-1]+2}; 其中a[i]==b[q], b[j]==a[p], 且p<i, q<j;
那么程序的时间复杂度为: O(m^2*n^2);
那么再找max{f[p-1][q-1]}的时候用了很多重复的操作,如果提前算出来时间复杂度会降为O(mn);
用二维数组max_a[i][j], 表示a[i]相等的b数组中前j(j<i)个数的最大匹配数的位置;
用二维数组max_b[i][j],表示b[i]相等的a数组中前j(j<i)个数的最大匹配数的位置;
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#define N 103
using namespace std;
int a[N], b[N], max_a[N][N], max_b[N][N], f[N][N];
int main()
{
int i, T, n, m, j;
scanf("%d", &T);
while(T--)
{
memset(max_a, 0, sizeof(max_a));
memset(max_b, 0, sizeof(max_b));
memset(f, 0, sizeof(f));
scanf("%d%d", &n, &m);
for(i=1; i<=n; i++)
scanf("%d", &a[i]);
for(i=1; i<=m; i++)
scanf("%d", &b[i]);
for(i=1; i<=n; i++)
for(j=1; j<=m; j++)
{
if(a[i]==b[j-1]) max_a[i][j]=j-1;
else max_a[i][j]=max_a[i][j-1];
}
for(i=1; i<=m; i++)
for(j=1; j<=n; j++)
{
if(b[i]==a[j-1]) max_b[i][j]=j-1;
else max_b[i][j]=max_b[i][j-1];
}
for(i=1; i<=n; i++)
for(j=1; j<=m; j++)
{
f[i][j]=max(f[i][j-1], f[i-1][j]);
int xx=max_a[i][j], yy=max_b[j][i];
if(xx>0&&yy>0&&f[yy-1][xx-1]+2>f[i][j]&&a[i]!=b[j])
f[i][j]=f[yy-1][xx-1]+2;
}
printf("%d\n", f[n][m]);
}
}