当前位置
- 字符串部分
- Trie树
- KMP
- AC自动机
导学
模式串匹配
模式串匹配,就是给定一个需要处理的文本串和一个需要在文本串中搜索的模式串,查询在该文本串中,模式串的有无情况、次数以及位置等。
常见模式匹配算法
-
朴素模式匹配算法——BF算法
用指针 i 指向文本串str1的字符str1[i],i 表示此时str1中比较的位置
用指针 j 指向模式串str2的字符str2[j],j表示模式串中已匹配的个数
-
从文本串str1[0]与模式串str2[0]开始
①若相等,则i++,j++,继续比较;②若失配,则i = i - j + 1, j = 0
i = i - j +1;//i指针发生回溯,将初始位置的下一个位置,作为下一次匹配的起点 j = 0;//从str2[0]重新匹配很明显,这样做虽然可行,但是失配后,i = i - j + 1,j = 0,即把模式串右移一位再从头开始比较,实际上效率很低。
那么,有没有什么办法能让模式串在失配后多右移几位?
并且尽量让模式串不从头开始匹配呢??我们引出了KMP算法。
-
-
KMP匹配算法
KMP算法由Knuth、Morris和Pratt三个人同时发现的,所以我们称之为KMP算法。它是一个很优秀的算法,将时间复杂度减少到了一个线性的水平。
我们可以很简单的想到,对于每一次匹配,当在str2[j]发生失配时,str2[0~j-1]其实是固定的。
KMP算法之所以有效就在于,它充分地利用了每一次失配能获得的信息,找到了一个更高效的指针移动方法。
接下来我们具体介绍。
KMP算法
如上所述,BF算法中,当str[i]失配时,i 需要回溯,并且 j 也得从0开始,即模式串仅右移一位再从头开始与文本串比较。
KMP中高效的指针移动方法,令文本串str1[i]失配时,i不发生回溯,j也不用从0再开始与str1比较,让模式串合理的高效的右移了n位(n>0),。
卖了好多关子,所以这个指针到底怎么移动的??
我们一步步来,先简单模拟一下。
eg1:
有文本串str1与模式串str2
初始:i = 0, j = 0
文本串str1:abcabdababcabc
模式串str2:abcabc
首先,前5位相同,i++, j ++;
当到第6位即str1[5]时,失配,此时 i = 5, j = 5。
i = 5, j = 5
文本串str1:abcab|dababcabc
模式串str2:abcab|c
直接给出结论:
我们可以将模式串右移3位,再继续比较
i = 5,j = 2
文本串str1:abcab|dababcabc
模式串str2: ab|cabc
我们仔细一看,实际上就是让 i = i = 5, j = 2,再继续比较
那么有好奇的同学就要问了,j为什么就等于2了?
这也就是KMP的关键点:如何确认每次失配,模式串指针j的变化是合理的??
指针j的变化——pmt与next数组
让我们在正式理解KMP算法之前,先弄清几个概念:
前缀:除最后一个字符外,字符串的所有头部子串
后缀:除第一个字符外,字符串的所有尾部子串
部分匹配值表(pmt):字符串中最大相同前后缀的长度 的记录表
PMT表的用法
-
首先,若已知失配的位置str[i]或str[j],我们可以确定已匹配的前缀部分
即确定了str1[i - j~i-1] 或者 str2[0~j-1] 的内容。
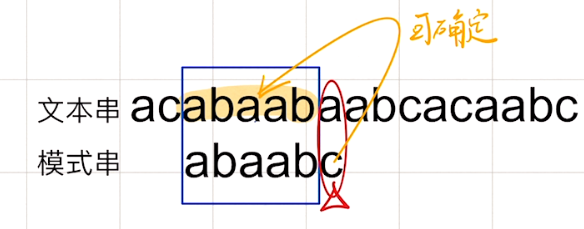
那么实际上我们只需要研究模式串str2本身,就能研究失配后的处理操作。
-
我们发现:当str2[j]失配时,我们应在已匹配的子串 str2[0~j-1] 中找出最长相同的前缀和后缀的部分,令它俩重合,再继续比较
也就是如下图所示,
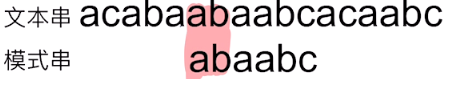
那这不就和部分匹配表关系上了!
我们这边给出该模式串的部分匹配表pmt数组
pmt[]: 0 1 2 3 4 5
模式串: a b a a b c部分匹配值:0 0 1 1 2 0
我们发现如下图移动后,i = i,j = pmt[j-1] = 2

-
也就是说当str2[j]失配时,我们取以j-1为结尾的模式串的部分匹配值
让 i = i,j = pmt[j-1] ,再继续让str1[i]和str2[j]匹配即可。
从pmt到next
由于当str2[j]失配时,我们取的是j-1的部分匹配值,也就是说最后一位部分匹配值实际上并没有意义,因此我们可以调整pmt数组整体向右移1位,使编程更方便。
我们将pmt[0] = -1,用next数组表示。
[]: 0 1 2 3 4 5 模式串: a b a a b c pmt: 0 0 1 1 2 0 next: -1 0 0 1 1 2我们可以发现next[0] = -1,next[1] = 0;
代码实现
为了让next数组更有实际意义,我们也常将next数组写作kmp数组。
获取mext数组
void get_next(){
int i = 0, j = -1;
next1[0] = -1;
while(i < b.length()){
//next1[1]=0 && 当相等时next1[++i] = ++j(右移一位)
if(j == -1 || b[i] == b[j] )//自己比自己
next1[++i] = ++j;
else //当第j位失配,回跳j,直到可以继续匹配或最终j=-1,next1[i++]=0
j = next1[j];
}
}
比较文本串
void KMP()
{
int i = 0, j = 0;
while(i < a.length())
{
if(j == -1 || a[i] == b[j]) //匹配成功,继续
i++,j++;
else j = next1[j]; //失配
if(j == b.length()) {//j == b.length()时,匹配成功
printf("%d
",i-b.length()+1);//i-b.length()+1即为第一个字母的位置
j = next1[j];//匹配成功后,j置为next1[j]
}
}
}